La Constante de Boltzmann est la valeur qui relie l'énergie cinétique moyenne d'un système thermodynamique ou d'un objet à sa température absolue. Bien qu'elles soient souvent confondues, la température et l'énergie ne sont pas le même concept.
La température est une mesure de l'énergie, mais pas de l'énergie elle-même. Avec la constante de Boltzmann, ils sont liés les uns aux autres de la manière suivante:
ETc = (3/2) kB T
Cette équation est valable pour une molécule de gaz parfait monoatomique de masse m, où ETc est son énergie cinétique donnée en Joules, kB est la constante de Boltzmann et T est la température absolue en Kelvin.
De cette manière, lorsque la température augmente, l'énergie cinétique moyenne par molécule de substance augmente également, comme cela devrait se produire. Et l'inverse se produit lorsque la température diminue, pouvant atteindre le point où si tout mouvement cesse, la température la plus basse possible ou le zéro absolu est atteint..
Lorsqu'on parle d'énergie cinétique moyenne, il faut se rappeler que l'énergie cinétique est associée au mouvement. Et les particules peuvent se déplacer de plusieurs façons, telles que se déplacer, tourner ou vibrer. Bien sûr, tous ne le feront pas de la même manière, et comme ils sont indénombrables, alors la moyenne est prise pour caractériser le système..
Certains états énergétiques sont plus probables que d'autres. Ce concept est d'une importance radicale en thermodynamique. L'énergie considérée dans l'équation ci-dessus est l'énergie cinétique de translation. La probabilité des états et sa relation avec la constante de Boltzmann seront discutées un peu plus tard..
En 2018, le Kelvin a été redéfini et avec lui la constante de Boltzmann, qui dans le système international est d'environ 1,380649 x 10-2. 3 J. K-1. La constante de Boltzmann, qui a été déterminée dans de nombreux laboratoires à travers le monde, par différentes méthodes, peut être beaucoup plus précise..
Index des articles
La célèbre constante doit son nom au physicien viennois Ludwig Boltzmann (1844-1906), qui a consacré sa vie de scientifique à l'étude du comportement statistique de systèmes à nombreuses particules, du point de vue de la mécanique newtonienne..
Bien qu'aujourd'hui l'existence de l'atome soit universellement acceptée, au dix-neuvième siècle, la croyance selon laquelle l'atome existait vraiment ou était un artifice avec lequel de nombreux phénomènes physiques étaient expliqués était en plein débat..
Boltzmann était un fervent défenseur de l'existence de l'atome et, à son époque, a fait face à de sévères critiques de son travail de la part de nombreux collègues, qui considéraient qu'il contenait des paradoxes insolubles..
Il a déclaré que les phénomènes observables aux niveaux macroscopiques pouvaient être expliqués par les propriétés statistiques des particules constituantes telles que les atomes et les molécules..
Ces critiques étaient peut-être dues à l'épisode profond de dépression qui le poussa à se suicider début septembre 1906, alors qu'il avait encore beaucoup à faire, puisqu'il était considéré comme l'un des grands physiciens théoriciens de son temps et qu'il y avait très peu de choses à faire. que d'autres scientifiques contribuent à corroborer la véracité de leurs théories.
Peu de temps après sa mort, de nouvelles découvertes sur la nature de l'atome et de ses particules constituantes se sont ajoutées pour donner raison à Boltzmann..
Maintenant, la constante de Boltzmann kB il a été introduit tel qu'il est connu aujourd'hui quelque temps après les travaux du physicien autrichien. C'est Max Planck, dans sa loi de l'émission du corps noir, œuvre qu'il présente en 1901, qui à cette époque lui donne la valeur de 1,34 x 10−23 J / K.
Vers 1933, une plaque avec la définition de l'entropie impliquant la célèbre constante a été ajoutée à la pierre tombale de Boltzmann à Vienne en hommage posthume: S = kB log W, équation qui sera discutée plus tard.
Aujourd'hui, la constante de Boltzmann est indispensable dans l'application des lois de la thermodynamique, de la mécanique statistique et de la théorie de l'information, domaines dont ce physicien triste fut un pionnier..
Les gaz peuvent être décrits en termes macroscopiques et également en termes microscopiques. Pour la première description, il y a des concepts tels que la densité, la température et la pression.
Cependant, il faut se rappeler qu'un gaz est composé de nombreuses particules, qui ont une tendance globale à un certain comportement. C'est cette tendance qui se mesure macroscopiquement. Une façon de déterminer la constante de Boltzmann est grâce à l'équation bien connue des gaz parfaits:
p.V = n. R. T
Ici p est la pression du gaz, V est son volume, n est le nombre de grains de beauté présents, R est la constante des gaz et T est la température. Dans une mole de gaz parfait, la relation suivante est remplie entre le produit p.V, et l'énergie cinétique translationnelle K l'ensemble est:
p.V = (2/3). K
Par conséquent, l'énergie cinétique est:
K = (3/2) n.R.T
En divisant par le nombre total de molécules présentes, que l'on appellera N, on obtient l'énergie cinétique moyenne d'une seule particule:
ETc = K / N
ETc= (3 / 2N) n.R.T
Dans une mole, il y a le nombre de particules d'Avogadro NÀ, et donc le nombre total de particules est N = nNA, restant:
ETc = (3 / 2nNÀ) n.R.T
Précisément le quotient R / NÀ est la constante de Boltzmann, étant ainsi montré que l'énergie cinétique de translation moyenne d'une particule ne dépend que de la température absolue T et non d'autres grandeurs telles que la pression, le volume ou encore le type de molécule:
ETc = (3/2) kB. T
Un gaz a une température donnée, mais cette température peut correspondre à différents états d'énergie interne. Comment visualiser cette différence?
Considérez le tirage simultané de 4 pièces et la manière dont elles peuvent tomber:
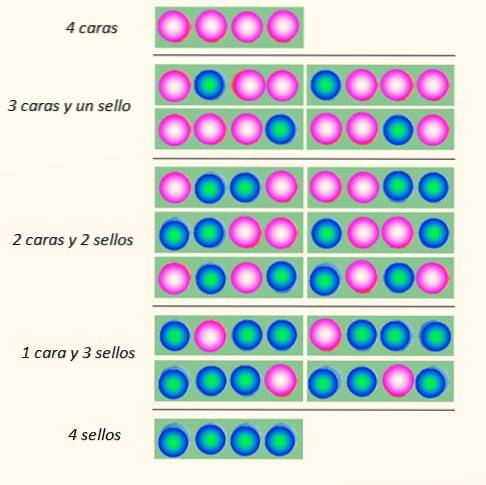
L'ensemble de pièces peut prendre un total de 5 états, qui sont considérés macroscopique, décrit dans la figure. Lequel de ces états, selon le lecteur, est le plus probable?
La réponse devrait être l'état de 2 têtes et 2 queues, car vous avez un total de 6 possibilités, sur les 16 illustrées sur la figure. Et 24 = 16. Ceux-ci sont équivalents aux états microscopique.
Et si 20 pièces sont lancées au lieu de 4? Il y aurait un total de 2vingt possibilités ou "états microscopiques". C'est un nombre beaucoup plus grand et plus difficile à manipuler. Pour faciliter la manipulation de grands nombres, les logarithmes sont très appropriés.
Or, ce qui semble évident, c'est que l'état avec le plus de désordre est le plus probable. Des états plus ordonnés comme 4 têtes ou 4 sceaux sont légèrement moins probables.
L'entropie d'un état macroscopique S est définie comme:
S = kB ln w
Où w est le nombre d'états microscopiques possibles du système et kB est la constante de Boltzmann. Quoi ln w est sans dimension, l'entropie a les mêmes unités que kB: Joule / K.
C'est la célèbre équation de la pierre tombale de Boltzmann à Vienne. Cependant, plus que l'entropie, ce qui est pertinent, c'est son changement:
ΔS = kB ln wdeux - kB ln w1 = kB ln (wdeux/ w1)
La valeur de la constante de Boltzmann est obtenue expérimentalement avec une extrême précision avec des mesures basées sur thermométrie acoustique, qui sont effectuées en utilisant la propriété qui établit la dépendance de la vitesse du son dans un gaz avec sa température.
En effet, la vitesse du son dans un gaz est donnée par:
Badiabatique = γp
Et ρ est la densité du gaz. Pour l'équation ci-dessus, p est la pression du gaz en question et γ est le coefficient adiabatique, dont la valeur pour un gaz donné se trouve dans les tableaux.
Les instituts de métrologie expérimentent également d'autres moyens de mesurer la constante, comme le Thermométrie de bruit Johnson, qui utilise des fluctuations thermiques qui se produisent au hasard dans les matériaux, en particulier les conducteurs.
Trouve:
a) Energie cinétique translationnelle moyenne ETc qui a une molécule de gaz idéal à 25 ºC
b) Énergie cinétique translationnelle K des molécules dans 1 mole de ce gaz
c) La vitesse moyenne d'une molécule d'oxygène à 25 ºC
moxygène = 16 x 10 -3 kg / mol
à) ETc = (3/2) k T = 1,5 x 1 380649 x 10-2. 3J. K-1 x 298 K = 6,2 x 10-vingt-et-un J
b) K = (3/2) n.R.T = 5 x 1 mol x 8,314 J / mol. K x 298 K = 3716 J
c) ETc = ½ mvdeux, en tenant compte du fait que la molécule d'oxygène est diatomique et que la masse molaire doit être multipliée par 2, on aura:
Trouvez le changement d'entropie lorsque 1 mole de gaz occupe un volume de 0,5 m3 s'agrandit pour occuper 1 m3.
ΔS = kB ln (wdeux/ w1)
wdeux= 2Nw1 (Il y avait 24 états microscopiques pour le tirage au sort des 4 pièces, tu te souviens?)
Où N est le nombre de particules présentes dans 0,5 mole de gaz 0,5 x NÀ:
ΔS = kB ln (2N w1/ w1) = kB ln 2N= kB 0,5 NÀ ln 2 = 2,88 J / K
Personne n'a encore commenté ce post.