
Système de coordonnées cylindriques, changement et exercices
le coordonnées cylindriques ils servent à localiser des points dans un espace tridimensionnel et consistent en une coordonnée radiale ρ, une coordonnée azimutale φ et une coordonnée de hauteur z.
Point P situé dans l'espace est projeté orthogonalement sur le plan XY donnant lieu au point P ' dans cet avion. La distance de l'origine au point P ' définit la coordonnée ρ, tandis que l'angle formé par l'axe X avec le rayon OP ' définit la coordonnée φ. Enfin, la coordonnée z est la projection orthogonale du point P sur l'axe Z. (voir figure 1).
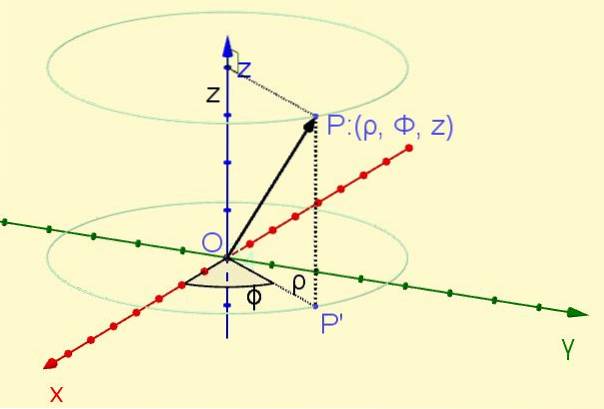
La coordonnée radiale ρ est toujours positive, la coordonnée azimutale φ varie de zéro radian à deux pi radians, tandis que la coordonnée z peut prendre n'importe quelle valeur réelle:
0 ≤ ρ < ∞
0 ≤ φ < 2π
- ∞ < z < + ∞
Index des articles
- 1 Changement de coordonnées
- 1.1 Base vectorielle en coordonnées cylindriques
- 2 exemples
- 2.1 Exemple 1
- 2.2 Exemple 2
- 3 exercices résolus
- 3.1 Exercice 1
- 3.2 Exercice 2
- 3.3 Exercice 3
- 3.4 Exercice 4
- 4 Références
Changement de coordonnées
Il est relativement facile d'obtenir les coordonnées cartésiennes (x, y, z) d'un point P à partir de ses coordonnées cylindriques (ρ, φ, z):
x = ρ cos (φ)
y = ρ sin (φ)
z = z
Mais il est également possible d'obtenir les coordonnées polaires (ρ, φ, z) à partir de la connaissance des coordonnées cartésiennes (x, y, z) d'un point P:
ρ = √ (xdeux + Ouideux)
φ = arctan (y / x)
z = z
Base vectorielle en coordonnées cylindriques
La base des vecteurs unitaires cylindriques est définie Uρ, Uφ, Uz.
Le vecteur Uρ est tangente à la droite φ = ctte et z = ctte (pointant radialement vers l'extérieur), le vecteur Uφ est tangente à la droite ρ = ctte et z = ctte et enfin Uz a la même direction de l'axe Z.
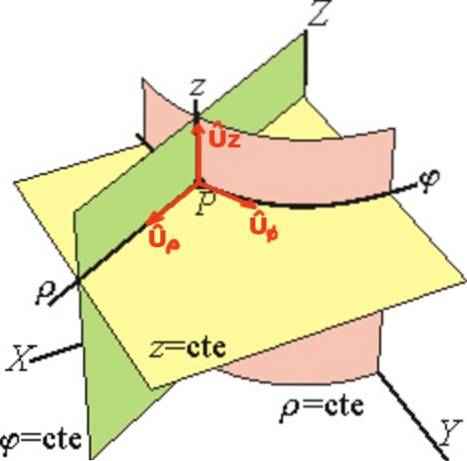
Dans la base d'unité cylindrique, le vecteur de position r d'un point P s'écrit vectoriellement comme ceci:
r = ρ Uρ + 0 Uφ + z Uz
D'autre part, un déplacement infinitésimal dr à partir du point P, il s'exprime comme suit:
rér = dρ Uρ + ρ dφ Uφ + dz Uz
De même, un élément infinitésimal du volume dV en coordonnées cylindriques est:
dV = ρ dρ dφ dz
Exemples
Il existe d'innombrables exemples d'utilisation et d'application de coordonnées cylindriques. En cartographie, par exemple, le projection cylindrique, basé précisément sur ces coordonnées. Il y a plus d'exemples:
Exemple 1
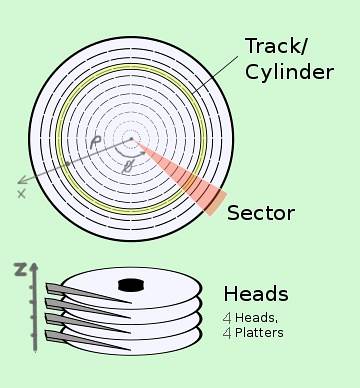
Les coordonnées cylindriques ont des applications en technologie. A titre d'exemple, nous avons le système CHS (Cylinder-Head-Sector) pour localiser des données sur un disque dur, qui se compose en fait de plusieurs disques:
- Le cylindre ou la piste correspond à la coordonnée ρ.
- Le secteur correspond à la position φ du disque qui tourne à haut vitesse angulaire.
- La tête correspond à la position z de la tête de lecture sur le disque correspondant.
Chaque octet d'information a une adresse précise en coordonnées cylindriques (C, S, H).
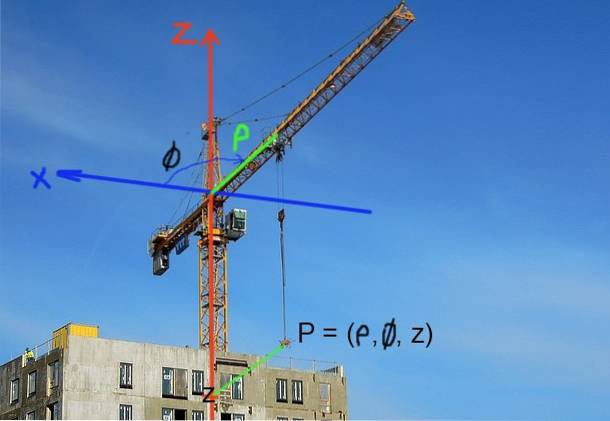
Exemple 2
Les grues de construction fixent la position de la charge en coordonnées cylindriques. La position horizontale est définie par la distance à l'axe ou à la flèche de la grue ρ et par sa position angulaire φ par rapport à un axe de référence. La position verticale de la charge est déterminée par la coordonnée z de la hauteur.
Exercices résolus
Exercice 1
Il y a des points P1 avec des coordonnées cylindriques (3, 120º, -4) et le point P2 avec des coordonnées cylindriques (2, 90º, 5). Trouvez le Distance euclidienne entre ces deux points.
Solution: Tout d'abord, nous recherchons les coordonnées cartésiennes de chaque point en suivant la formule donnée ci-dessus.
P1 = (3 * cos 120º, 3 * sin 120º, -4) = (-1,5, 2,60, -4)
P2 = (2 * cos 90º, 2 * sin 90º, 5) = (0, 2, 5)
La distance euclidienne entre P1 et P2 est:
d (P1, P2) = √ ((0 - (-1,5))deux+(2 - 2,60)deux+(5 - (- 4))deux ) = ...
… √ (2,25 + 0,36 + 81) = 9,14
Exercice 2
Le point P a des coordonnées cartésiennes (-3, 4, 2). Trouvez les coordonnées cylindriques correspondantes.
Solution: Nous procédons à la recherche des coordonnées cylindriques en utilisant les relations données ci-dessus:
ρ = √ (xdeux + Ouideux) = √ ((- 3)deux + 4deux) = √ (9 + 16) = √ (25) = 5
φ = arctan (y / x) = arctan (4 / (- 3)) = -53,13 ° + 180 ° = 126,87 °
z = 2
Il ne faut pas oublier que la fonction arc tangente est à valeurs multiples avec une périodicité de 180 °. De plus, l'angle φ doit appartenir au deuxième quadrant, puisque les coordonnées x et y du point P sont dans ce quadrant. C'est la raison pour laquelle 180º a été ajouté au résultat φ.
Exercice 3
Exprimer en coordonnées cylindriques et en coordonnées cartésiennes la surface d'un cylindre de rayon 2 et dont l'axe coïncide avec l'axe Z.
Solution: Il est entendu que le cylindre a une extension infinie dans la direction z, donc l'équation de ladite surface en coordonnées cylindriques est:
ρ = 2
Pour obtenir l'équation cartésienne de la surface cylindrique, le carré des deux membres de l'équation précédente est pris:
ρdeux = 4
Nous multiplions par 1 les deux membres de l'égalité précédente et appliquons la identité trigonométrique fondamentale (sendeux(φ) + cosdeux(φ) = 1):
1 * ρdeux = 1 * 4
(sendeux(φ) + cosdeux(φ)) * ρdeux = 1 * 4
La parenthèse est développée pour obtenir:
(ρ sin (φ))deux + (ρ cos (φ))deux = 4
Nous rappelons que la première parenthèse (ρ sin (φ)) est la coordonnée y d'un point en coordonnées polaires, tandis que les parenthèses (ρ cos (φ)) représentent la coordonnée x, de sorte que nous avons l'équation du cylindre en coordonnées cartésiennes:
Ouideux + Xdeux = 2deux
L'équation précédente ne doit pas être confondue avec celle d'un cercle dans le plan XY, car dans ce cas elle ressemblerait à ceci: ydeux + Xdeux = 2deux ; z = 0.
Exercice 4
Un cylindre de rayon R = 1 m et de hauteur H = 1m a sa masse répartie radialement selon l'équation suivante D (ρ) = C (1 - ρ / R) où C est une constante de valeur C = 1 kg / m3. Trouvez la masse totale du cylindre en kilogrammes.
Solution: La première chose est de se rendre compte que la fonction D (ρ) représente la masse volumique volumique, et que la masse volumique est répartie dans des coques cylindriques de densité décroissante du centre vers la périphérie. Un élément de volume infinitésimal selon la symétrie du problème est:
dV = ρ dρ 2π H
Par conséquent, la masse infinitésimale d'une coque cylindrique sera:
dM = D (ρ) dV
Par conséquent, la masse totale du cylindre sera exprimée par ce qui suit Intégrale définie:
M = ∫ou alorsR D (ρ) dV = ∫ou alorsR C (1 - ρ / R) ρ dρ 2π H = 2π H C ∫ou alorsR (1 - ρ / R) ρ dρ
La solution de l'intégrale indiquée n'est pas difficile à obtenir, son résultat étant:
∫ou alorsR (1 - ρ / R) ρ dρ = (⅙) Rdeux
En incorporant ce résultat dans l'expression de la masse du cylindre, on obtient:
M = 2π H C (⅙) Rdeux = ⅓ π H C Rdeux =
⅓ π 1 m * 1 kg / m3* 1 mdeux = π / 3 kg ≈ 1,05 kg
Les références
- Arfken G et Weber H. (2012). Méthodes mathématiques pour les physiciens. Un guide complet. 7e édition. Presse académique. ISBN 978-0-12-384654-9
- Calcul cc. Résolution des problèmes de coordonnées cylindriques et sphériques. Récupéré de: calculo.cc
- Weisstein, Eric W. «Coordonnées cylindriques». De MathWorld-A Wolfram Web. Récupéré de: mathworld.wolfram.com
- Wikipédia. Système de coordonnées cylindriques. Récupéré de: en.wikipedia.com
- Wikipédia. Champs vectoriels en coordonnées cylindriques et sphériques. Récupéré de: en.wikipedia.com


Personne n'a encore commenté ce post.