
Quelle est la différence entre le chemin et le déplacement?
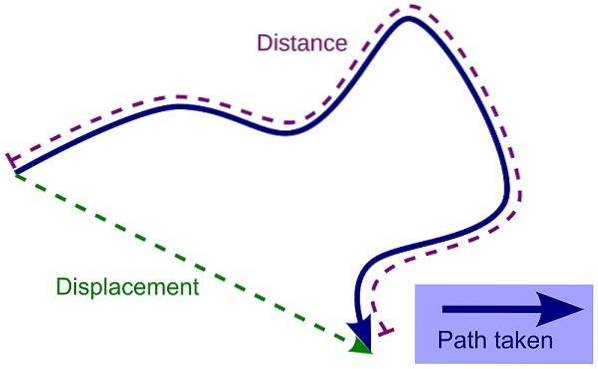
La différence principale entre trajectoire et déplacement est que ce dernier est la distance et la direction parcourue par un objet, tandis que le premier est le chemin ou la forme que prend le mouvement de cet objet.
Cependant, pour voir plus clairement les différences entre déplacement et trajectoire, il vaut mieux préciser sa conceptualisation à travers des exemples qui permettent une meilleure compréhension des deux termes..
Déplacement
Elle s'entend comme la distance et la direction parcourue par un objet en tenant compte de sa position initiale et de sa position finale, toujours en ligne droite. Pour son calcul, comme il s'agit d'une grandeur vectorielle, les mesures de longueur appelées centimètres, mètres ou kilomètres sont utilisées..
La formule pour calculer le déplacement est définie comme suit:
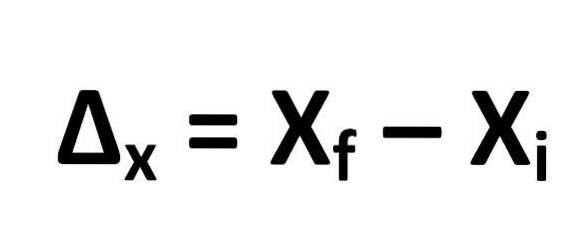
D'où il résulte que:
- ΔX = déplacement
- XF = position finale de l'objet
- Xje = position initiale de l'objet
Exemple de déplacement
1- Si un groupe d'enfants est au début d'un parcours, dont la position initiale est de 50m, se déplaçant en ligne droite, déterminer le déplacement à chacun des points XF .
- XF = 120 m
- XF = 90 m
- XF = 60 m
- XF = 40 m
2- Les données du problème sont extraites en substituant les valeurs de Xdeux et X1 dans la formule de décalage:
- ΔX = ?
- Xje = 50 m
- ΔX = XF - Xje
- ΔX = 120 m - 50 m = 70 m
3- Dans cette première approche on dit que ΔX est égal à 120m, ce qui correspond à la première valeur trouvée de XF, moins 50m qui est la valeur de Xje, Le résultat est de 70 m, c'est-à-dire qu'en atteignant 120 m parcourus, le déplacement était de 70 m à droite.
4- Nous procédons de la même manière pour résoudre les valeurs de b, c et d
- ΔX = 90 m - 50 m = 40 m
- ΔX = 60 m - 50 m = 10 m
- ΔX = 40 m - 50 m = - 10 m
Dans ce cas, le déplacement nous a donné négatif, cela signifie que la position finale est dans la direction opposée à la position initiale.
Trajectoire
C'est l'itinéraire ou la ligne déterminée par un objet lors de son mouvement et son évaluation dans le système international, adopte généralement des formes géométriques telles que la ligne, la parabole, le cercle ou l'ellipse). Il est identifié par une ligne imaginaire et comme il s'agit d'une grandeur scalaire, il est mesuré en mètres.
Il est à noter que pour calculer la trajectoire il faut savoir si le corps est au repos ou en mouvement, c'est-à-dire qu'il est soumis au référentiel que l'on sélectionne.
L'équation pour calculer la trajectoire d'un objet dans le système international est donnée par:
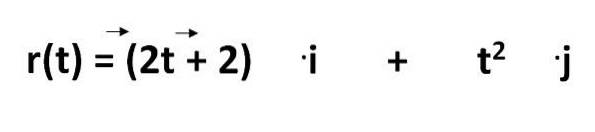
Dont nous devons:
- r (t) = est l'équation du chemin
- 2t - 2 et tdeux = représente les coordonnées en fonction du temps
- .moi et .j = sont les vecteurs unitaires
Pour comprendre le calcul du chemin parcouru par un objet, nous allons développer l'exemple suivant:
- Calculez l'équation des trajectoires des vecteurs de position suivants:
- r (t) = (2t + 7) .i + tdeux .j
- r (t) = (t - 2) .i + 2t .j
Première étape: comme une équation de chemin est fonction de X, pour ce faire définissez les valeurs de X et Y respectivement dans chacun des vecteurs proposés:
1- Résoudre le premier vecteur de position:
- r (t) = (2t + 7) .i + tdeux .j
2- Ty = f (x), où X est donné par le contenu du vecteur unitaire .i et Y sont donnés par le contenu du vecteur unitaire .j:
- X = 2t + 7
- Y = tdeux
3- y = f (x), c'est-à-dire que le temps ne fait pas partie de l'expression donc nous devons le résoudre, nous avons:
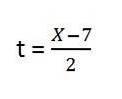
4- Nous substituons le jeu en Y. Il reste:
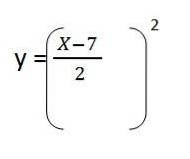
5- Nous résolvons le contenu des parenthèses et nous avons l'équation du chemin résultant pour le premier vecteur unitaire:
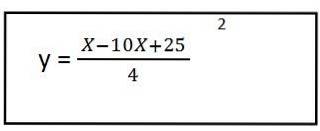
Comme nous pouvons le voir, cela nous a donné une équation au deuxième degré, cela signifie que la trajectoire a la forme d'une parabole.
Deuxième étape: On procède de la même manière pour calculer la trajectoire du deuxième vecteur unitaire
r (t) = (t - 2) .i + 2t .j
- X = t - 2
- Y = 2t
2- En suivant les étapes que nous avons vu précédemment y = f (x), il faut effacer l'heure car elle ne fait pas partie de l'expression, on se retrouve avec:
- t = X + 2
3- Nous substituons le jeu en Y, restant:
- y = 2 (X + 2)
4- En résolvant les parenthèses, nous avons l'équation de la trajectoire résultante pour le deuxième vecteur unitaire:
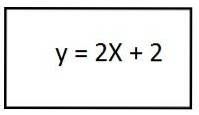
Dans cette procédure, le résultat était une ligne droite, qui nous indique que la trajectoire a une forme rectiligne.
Une fois les concepts de déplacement et de trajectoire compris, on peut déduire le reste des différences qui existent entre les deux termes.
Plus de différences entre déplacement et trajectoire
Déplacement
- C'est la distance et la direction parcourue par un objet en tenant compte de sa position initiale et de sa position finale.
- Ça se passe toujours en ligne droite.
- Il est reconnu par une flèche.
- Utiliser des mesures de longueur (centimètre, mètre, kilomètre).
- C'est une quantité vectorielle.
- Tenez compte de la direction parcourue (à droite ou à gauche)
- Il ne tient pas compte du temps passé pendant la visite.
- Ne dépend pas d'un système de référence.
- Lorsque le point de départ est le même point de départ, le décalage est nul.
- Le module doit coïncider avec l'espace à parcourir tant que le chemin est une ligne droite et qu'il n'y a pas de changement de direction à suivre.
- Le module a tendance à augmenter ou à diminuer au fur et à mesure que le mouvement se produit, en gardant à l'esprit la trajectoire.
Trajectoire
C'est la trajectoire ou la ligne déterminée par un objet lors de son mouvement. Adopte des formes géométriques (droites, paraboliques, circulaires ou elliptiques).
- Il est représenté par une ligne imaginaire.
- Il est mesuré en mètres.
- C'est une quantité scalaire.
- Il ne prend pas en compte la direction parcourue.
- Considérez le temps passé pendant la visite.
- Dépend d'un système de référence.
- Lorsque le point de départ ou la position initiale est le même que la position finale, la trajectoire est donnée par la distance parcourue.
- La valeur de la trajectoire coïncide avec le module du vecteur de déplacement, si la trajectoire résultante est une ligne droite, mais il n'y a pas de changement dans la direction à suivre.
- Augmente toujours lorsque le corps bouge, quelle que soit la trajectoire.
Les références
- Alvarado, N. (1972) Physique. Première année de science. Éditorial Fotoprin C.A. Venezuela.
- Fernández, M; Fidalgo, J. (2016). Physique et Chimie 1er Baccalauréat. Éditions Paraninfo, S.A. Espagne.
- Institut guatémaltèque d'éducation radiophonique. (2011) Physique fondamentale. Premier semestre du groupe Zaculeu. Guatemala.
- Fernández, P. (2014) Domaine scientifique et technologique. Éditions Paraninfo. S.A. Espagne.
- Déplacement vectoriel de Fisica Lab (2015). Récupéré de: fisicalab.com.
- Exemples de. (2013) Déplacement. Récupéré de: examplesde.com.
- Living Room Home Project (2014) Qu'est-ce que le déplacement? Récupéré de: salonhogar.net.
- Laboratoire de physique (2015) Concept de trajectoire et équation de position. Récupéré de: fisicalab.com.


Personne n'a encore commenté ce post.