
Dérivée du calcul cotangent, preuve, exercices
La dérivé de la cotangente est égal à l'opposé du carré de la cosécante "-Cscdeux». Cette formule obéit aux lois de la dérivée par définition et à la différenciation des fonctions trigonométriques. Il est noté comme suit:
d (ctg u) = -cscdeux ou alors . du
Où "du" symbolise l'expression dérivée de la fonction argument, par rapport à la variable indépendante.

Index des articles
- 1 Comment est-il calculé?
- 2 Caractéristiques de la fonction cotangente
- 2.1 Asymptotes verticales
- 2.2 Domaine
- 2.3 Gamme
- 2.4 Fréquence
- 2.5 Comportement
- 3 Démo
- 3.1 Preuve différentielle trigonométrique
- 3.2 Preuve par définition de dérivé
- 4 exercices résolus
- 4.1 Exercice 1
- 4.2 Exercice 2
- 5 Références
Comment est-il calculé?
La procédure pour développer ces dérivés est assez simple. Tout ce que vous avez à faire est d'identifier correctement l'argument et le type de fonction qu'il représente..
Par exemple, l'expression Ctg (f / g) a une division dans son argument. Cela nécessitera une différenciation par rapport à U / V, après avoir développé la dérivée de la cotangente.
La cotangente est l'inverse de la tangente. Algébriquement, cela signifie que:
(1 / tg x) = ctg x
Ctg x = Cos x / Sen x
Il est incorrect de dire que la fonction cotangente est "l'inverse" de la tangente. En effet, la fonction tangente inverse par définition est tangente d'arc.
(Tg-1 x) = arctg x
Selon la trigonométrie de Pythagore, la cotangente est impliquée dans les sections suivantes:
Ctg x = (cos x) / (sin x)
Ctgdeux x + 1 = Cscdeux X
Selon la trigonométrie analytique, il répond aux identités suivantes:
Ctg (a + b) = (1 - tg a. Tg b) / (tg a + tg b)
Ctg (a - b) = (1 + tg a. Tg b) / (tg a - tg b)
Ctg (2a) = (1 - tgdeux a) / (2tg a)
Caractéristiques de la fonction cotangente
Il est nécessaire d'analyser différentes caractéristiques de la fonction f (x) = ctg x afin de définir les aspects nécessaires à l'étude de sa différentiabilité et de son application.
Asymptotes verticales
La fonction cotangente n'est pas définie sur les valeurs qui mettent à zéro l'expression "Senx". En raison de son équivalent Ctg x = (cos x) / (sin x), il aura une indétermination dans tout «nπ» avec n appartenant aux entiers.
Autrement dit, dans chacune de ces valeurs de x = nπ, il y aura une asymptote verticale. À mesure que vous vous approchez de la gauche, la valeur de la cotangente diminuera rapidement, et à mesure que vous vous approcherez de la droite, la fonction augmentera indéfiniment.
Domaine
Le domaine de la fonction cotangente est exprimé par l'ensemble x ∈ R / x ≠ nπ, n ∈ Z. Ceci est lu comme "x appartenant à l'ensemble des nombres réels tels que x est différent de nπ, avec n appartenant à l'ensemble des nombres entiers".
Rang
La plage de la fonction cotangente va de moins à plus l'infini. Par conséquent, on peut conclure que sa plage est l'ensemble des nombres réels R.
La fréquence
La fonction cotangente est périodique et sa période est égale à π. De cette façon, l'égalité Ctg x = Ctg (x + nπ) est remplie, où n appartient à Z.
Comportement
C'est une fonction étrange, puisque Ctg (-x) = - Ctg x. De cette manière, on sait que la fonction présente une symétrie par rapport à l'origine des coordonnées. Il présente également une diminution de chaque intervalle situé entre 2 asymptotes verticales successives.
Il n'a pas de valeurs maximales ou minimales, car ses approximations des asymptotes verticales présentent des comportements où la fonction augmente ou diminue indéfiniment.
Les zéros ou racines de la fonction cotangente se trouvent à des multiples impairs de π / 2. Cela signifie que Ctg x = 0 est valable pour les valeurs de la forme x = nπ / 2 avec n entier impair.
Manifestation
Il y a 2 façons de prouver la dérivée de la fonction cotangente.
Preuve différentielle trigonométrique
La dérivée de la fonction cotangente de son équivalent en sinus et cosinus est prouvée.
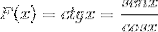
Il est traité comme le dérivé d'une division de fonctions
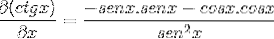
Après avoir dérivé, les facteurs sont regroupés et le but est d'imiter les identités pythagoriciennes
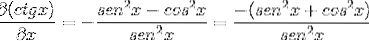
En substituant les identités et en appliquant la réciprocité, l'expression est obtenue
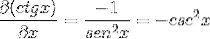
Preuve par définition de dérivé
L'expression suivante correspond par définition au dérivé. Où la distance entre 2 points de la fonction s'approche de zéro.
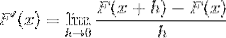
En remplaçant la cotangente, nous avons:
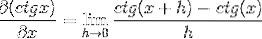
Les identités sont appliquées pour la somme des arguments et la réciprocité
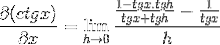
La fraction du numérateur est traditionnellement opérée
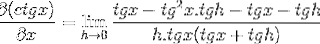
En éliminant les éléments opposés et en prenant un facteur commun, on obtient
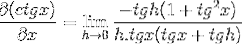
Appliquer les identités pythagoriciennes et la réciprocité, nous devons
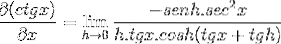
Les éléments évalués en x sont constants par rapport à la limite, ils peuvent donc laisser l'argument de this. Ensuite, les propriétés des limites trigonométriques sont appliquées.
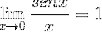
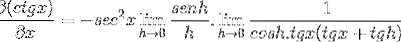
La limite est évaluée
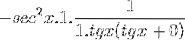
Ensuite, il est factorisé jusqu'à ce que la valeur souhaitée soit atteinte
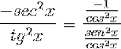
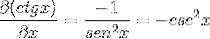
La dérivée de la cotangente est ainsi démontrée comme l'opposé du carré de la cosécante.
Exercices résolus
Exercice 1
En vous basant sur la fonction f (x), définissez l'expression f '(x)
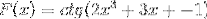
La dérivation correspondante est appliquée en respectant la règle de la chaîne
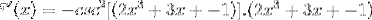
Dériver l'argument
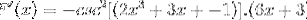
Parfois, il est nécessaire d'appliquer des identités réciproques ou trigonométriques pour adapter les solutions.
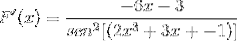
Exercice 2
Définir l'expression différentielle correspondant à F (x)
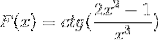
Selon la formule de dérivation et en respectant la règle de la chaîne
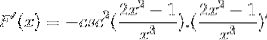
L'argument est dérivé, tandis que le reste reste le même
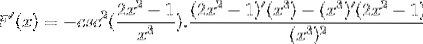
Dériver tous les éléments
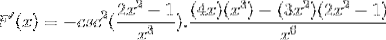
Fonctionnant de manière traditionnelle les produits d'une même base
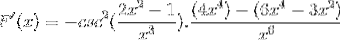
Les éléments égaux sont ajoutés et le facteur commun est extrait
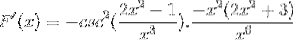
Les panneaux sont simplifiés et exploités. Céder la place à une expression entièrement dérivée
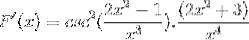
Les références
- Série trigonométrique, volume 1. A. Zygmund. Cambridge University Press, 2002
- Calcul d'une variable unique. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 novembre 2008
- Calcul avec trigonométrie et géométrie analytique. John H. Saxon, John Saxon, Frank Wang, Diana Harvey. Éditeurs Saxon, 1988
- Analyse multivariée. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 décembre. 2010
- Dynamique des systèmes: modélisation, simulation et contrôle des systèmes mécatroniques. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 mars 2012
- Calcul: mathématiques et modélisation. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 janv. 1999



Personne n'a encore commenté ce post.