
Dérivés successifs (avec exercices résolus)
le dérivés successifs sont les dérivées d'une fonction après la dérivée seconde. Le processus pour calculer les dérivées successives est le suivant: nous avons une fonction f, que nous pouvons déduire et ainsi obtenir la fonction dérivée f '. On peut dériver à nouveau cette dérivée de f, en obtenant (f ')'.
Cette nouvelle fonction est appelée la dérivée seconde; toutes les dérivées calculées à partir de la seconde sont successives; Celles-ci, également appelées d'ordre supérieur, ont de grandes applications, telles que donner des informations sur le tracé du graphique d'une fonction, le test de la dérivée seconde pour les extrêmes relatifs et la détermination de séries infinies.

Index des articles
- 1 Définition
- 1.1 Exemple 1
- 1.2 Exemple 2
- 2 Vitesse et accélération
- 2.1 Exemple 1
- 2.2 Exemple 2
- 3 applications
- 3.1 Dérivation implicite
- 3.2 Exemple
- 3.3 Extrêmes relatifs
- 3.4 Exemple
- 3.5 Série Taylor
- 3.6 Exemple
- 4 Références
Définition
En utilisant la notation de Leibniz, nous avons que la dérivée d'une fonction "y" par rapport à "x" est dy / dx. Pour exprimer la deuxième dérivée de "y" en utilisant la notation de Leibniz, nous écrivons comme suit:

En général, on peut exprimer les dérivées successives comme suit avec la notation de Leibniz, où n représente l'ordre de la dérivée.

Les autres notations utilisées sont les suivantes:
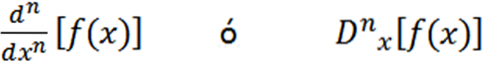
Quelques exemples où nous pouvons voir les différentes notations sont:
Exemple 1
Obtenez toutes les dérivées de la fonction f définie par:
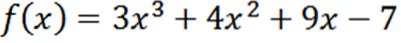
En utilisant les techniques de dérivation habituelles, nous avons que la dérivée de f est:

En répétant le processus, nous pouvons obtenir la deuxième dérivée, la troisième dérivée et ainsi de suite.
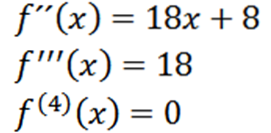
Notez que la quatrième dérivée est zéro et la dérivée de zéro est zéro, nous avons donc:

Exemple 2
Calculez la quatrième dérivée de la fonction suivante:
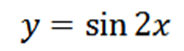
En dérivant la fonction donnée, nous avons comme résultat:
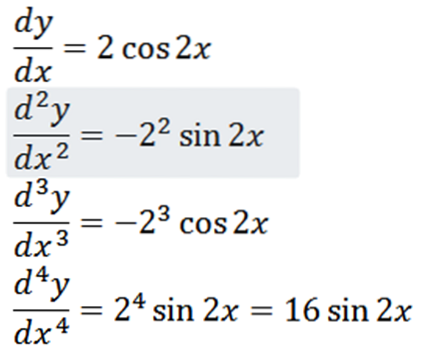
Vitesse et accélération
L'une des motivations qui a conduit à la découverte du dérivé était la recherche de la définition de la vitesse instantanée. La définition formelle est la suivante:
Soit y = f (t) une fonction dont le graphe décrit la trajectoire d'une particule à un instant t, alors sa vitesse à un instant t est donnée par:

Une fois la vitesse d'une particule obtenue, on peut calculer l'accélération instantanée, qui est définie comme suit:
L'accélération instantanée d'une particule dont le trajet est donné par y = f (t) est:

Exemple 1
Une particule se déplace le long d'une ligne selon la fonction de position:

Où «y» est mesuré en mètres et «t» en secondes.
- A quel instant est sa vitesse 0?
- A quel instant est son accélération 0?
Lors de la dérivation de la fonction de position "y", nous avons que sa vitesse et son accélération sont données respectivement par:

Pour répondre à la première question, il suffit de déterminer quand la fonction v devient nulle; c'est:
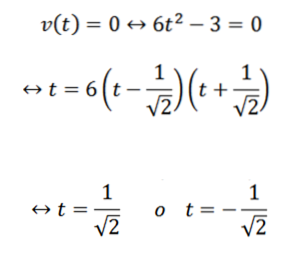
Nous procédons de manière analogue à la question suivante:

Exemple 2
Une particule se déplace le long d'une ligne selon l'équation de mouvement suivante:

Déterminez "t, y" et "v" quand a = 0.
Sachant que la vitesse et l'accélération sont données par

Nous procédons à dériver et obtenir:

En faisant a = 0, nous avons:
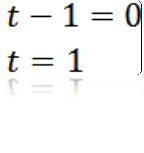
D'où on peut déduire que la valeur de t pour que a soit égal à zéro est t = 1.
Ensuite, en évaluant la fonction de position et la fonction de vitesse à t = 1, nous avons:

Applications
Dérivation explicite
Des dérivées successives peuvent également être obtenues par dérivation implicite.
Exemple
Étant donné l'ellipse suivante, trouvez «y»:

En dérivant implicitement par rapport à x, nous avons:
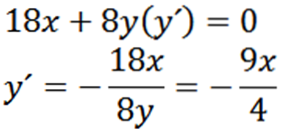
Ensuite, la redéfinition implicite par rapport à x nous donne:

Enfin, nous avons:
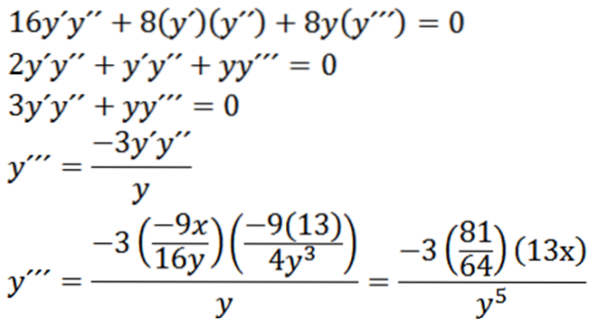
Extrêmes relatifs
Une autre utilisation que l'on peut donner aux dérivées du second ordre est dans le calcul des extrêmes relatifs d'une fonction.
Le critère de la première dérivée pour les extrêmes locaux nous dit que, si nous avons une fonction continue f dans un intervalle (a, b) et qu'il existe un c qui appartient audit intervalle tel que f 's'annule dans c (c'est-à-dire que c est un point critique), l'un des trois cas peut se produire:
- Si f '(x)> 0 pour tout x appartenant à (a, c) et f' (x)<0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
- Si f '(x) < 0 para cualquier x perteneciente a (a,c) y f'(x)>0 pour x appartenant à (c, b), alors f (c) est un minimum local.
- Si f '(x) a le même signe dans (a, c) et dans (c, b), cela implique que f (c) n'est pas un extrême local.
En utilisant le critère de la dérivée seconde, nous pouvons savoir si un nombre critique d'une fonction est un maximum local ou un minimum, sans avoir à voir quel est le signe de la fonction dans les intervalles susmentionnés..
Le second critère de dérive nous dit que si f '(c) = 0 et que f "(x) est continue dans (a, b), il arrive que si f" (c)> 0 alors f (c) soit un local minimum et si f "(c) < 0 entonces f(c) es un máximo local.
Si f "(c) = 0, on ne peut rien conclure.
Exemple
Étant donné la fonction f (x) = x4 + (4/3) x3 - 4xdeux, trouver les maxima et minima relatifs de f en appliquant le critère de dérivée seconde.
Nous calculons d'abord f '(x) et f "(x) et nous avons:
f '(x) = 4x3 + 4xdeux - 8x
f "(x) = 12xdeux + 8x - 8
Maintenant, f '(x) = 0 si, et seulement si 4x (x + 2) (x - 1) = 0, et cela se produit lorsque x = 0, x = 1 ou x = - 2.
Pour déterminer si les nombres critiques obtenus sont des extrêmes relatifs, il suffit d'évaluer en f "et donc d'observer son signe.
f "(0) = - 8, donc f (0) est un maximum local.
f "(1) = 12, donc f (1) est un minimum local.
f "(- 2) = 24, donc f (- 2) est un minimum local.
Série Taylor
Soit f une fonction définie comme suit:
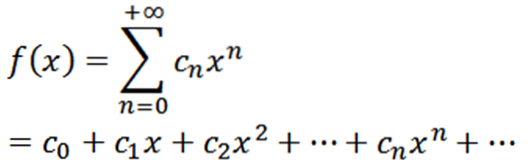
Cette fonction a un rayon de convergence R> 0 et a des dérivées de tous les ordres en (-R, R). Les dérivées successives de f nous donnent:
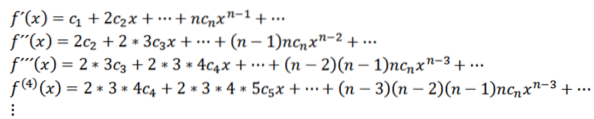
En prenant x = 0, nous pouvons obtenir les valeurs de cn sur la base de ses dérivés comme suit:
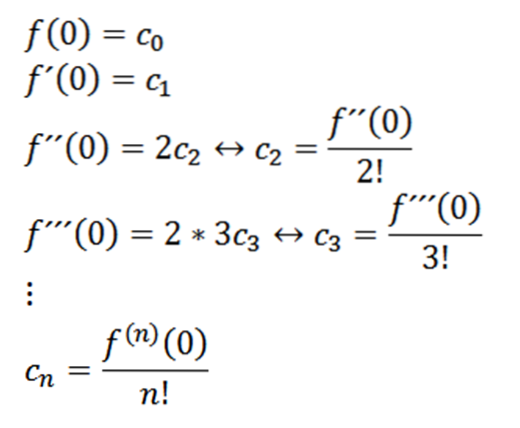
Si nous prenons n = 0 comme fonction f (c'est-à-dire f ^ 0 = f), alors nous pouvons réécrire la fonction comme suit:
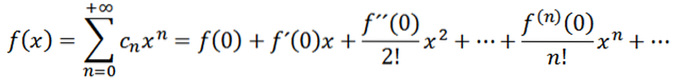
Considérons maintenant la fonction comme une série de puissances à x = a:
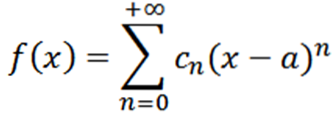
Si nous effectuons une analyse analogue à la précédente, nous aurions que nous puissions écrire la fonction f comme:
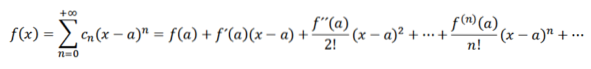
Ces séries sont appelées séries de Taylor de f à a. Quand a = 0, nous avons le cas particulier qui s'appelle la série Maclaurin. Ce type de série est d'une grande importance mathématique en particulier dans l'analyse numérique, car grâce à ceux-ci, nous pouvons définir des fonctions dans les ordinateurs tels que eX , sin (x) et cos (x).
Exemple
Obtenez la série Maclaurin pour eX.
Notez que si f (x) = eX, puis f(n)(x) = eX et f(n)(0) = 1, donc votre série Maclaurin est:
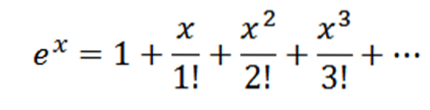
Les références
- Frank Ayres, J., et Mendelson, E. (s.f.). Calcul 5ed. Mc Graw Hill.
- Leithold, L. (1992). Le calcul avec la géométrie analytique. HARLA, S.A.
- Purcell, E. J., Varberg, D. et Rigdon, S. E. (2007). Calcul. Mexique: Pearson Education.
- Saenz, J. (2005). Calcul différentiel. Hypoténuse.
- Saenz, J. (s.f.). Calcul intégral. Hypoténuse.


Personne n'a encore commenté ce post.