L'équation générale d'une droite L est la suivante: Ax + By + C = 0, où A, B et C sont des constantes, x est la variable indépendante et et la variable dépendante.
La pente d'une droite, généralement désignée par la lettre m, passant par les points P = (x1, y1) et Q = (x0, y0) est le quotient m suivant: = (y1-y0) / (x1 -x0 ).
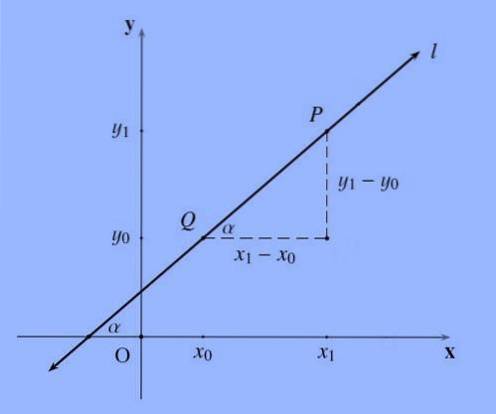
La pente d'une droite, représente d'une certaine manière l'inclinaison; Plus formellement, la pente d'une ligne est la tangente de l'angle qu'elle forme avec l'axe X..
Il est à noter que l'ordre dans lequel les points sont nommés est indifférent, puisque (y0-y1) / (x0-x1) = - (y1-y0) / (- (x1-x0)) = (y1-y0) / (x1-x0).
Si l'on connaît deux points par lesquels passe une ligne, il est facile de calculer sa pente. Mais que faire si ces points ne sont pas connus?
Étant donné l'équation générale d'une droite Ax + By + C = 0, sa pente est m = -A / B.
Comme la pente de la droite est de 2/3, alors l'égalité -A / B = 2/3 est établie, avec laquelle nous pouvons voir que A = -2 et B = 3. Donc l'équation générale d'une droite de pente égale à 2/3 est -2x + 3y + C = 0.
Il convient de préciser que si A = 2 et B = -3 sont choisis, la même équation sera obtenue. En effet, 2x-3y + C = 0, qui est égal au précédent multiplié par -1. Le signe de C n'a pas d'importance car c'est une constante générale.
Une autre observation que l'on peut faire est que pour A = -4 et B = 6 la même droite est obtenue, malgré le fait que leur équation générale est différente. Dans ce cas, l'équation générale est -4x + 6y + C = 0.
La réponse est oui. Si la pente d'une droite est connue, il existe deux façons, en plus de la précédente, de trouver l'équation générale.
Pour cela, l'équation point-pente et l'équation cisaillement-pente sont utilisées..
-L'équation Point-Pente: si m est la pente d'une droite et P = (x0, y0) un point par lequel elle passe, alors l'équation y-y0 = m (x-x0) est appelée équation Point-Pente.
-L'équation Shear-Slope: si m est la pente d'une ligne et (0, b) est la coupe de la ligne avec l'axe Y, alors l'équation y = mx + b est appelée l'équation Shear-Slope.
En utilisant le premier cas, on obtient que l'équation Point-Pente d'une droite dont la pente est 2/3 est donnée par l'expression y-y0 = (2/3) (x-x0).
Pour arriver à l'équation générale, multipliez par 3 des deux côtés et tous les termes sont regroupés d'un côté de l'égalité, avec laquelle on obtient que -2x + 3y + (2 × 0-3y0) = 0 est l'équation générale de la ligne, où C = 2 × 0-3y0.
Si le deuxième cas est utilisé, on obtient que l'équation Cut-Slope d'une droite dont la pente est 2/3 est y = (2/3) x + b.
Encore une fois, en multipliant par 3 des deux côtés et en regroupant toutes les variables, nous obtenons -2x + 3y-3b = 0. Cette dernière est l'équation générale de la droite où C = -3b.
En fait, en regardant de près les deux cas, on peut voir que le second cas est simplement un cas particulier du premier (lorsque x0 = 0).
Personne n'a encore commenté ce post.