le équations au premier degré ou linéaires avec une inconnue sont ceux qui peuvent être exprimés comme la somme de deux termes, comme suit:
hache + b = 0
Où a et b, avec à ≠ 0, sont des nombres réels R ou également complexes C.Pour le résoudre, les termes sont transposés, ce qui signifie changer les termes d'un côté de l'égalité à l'autre.
Pour résoudre l'inconnu, le terme + b est transposé, qui doit aller du côté droit de l'égalité avec le signe changé.
ax = -b
Ensuite, la valeur de x est effacée, comme ceci:
x = - b / a
A titre d'exemple, nous allons résoudre l'équation suivante:
6x - 5 = 4
Nous transposons le terme -5 sur le côté droit avec un signe modifié:
6x = 4 + 5
Cela équivaut à ajouter 5 aux deux côtés de l'équation d'origine:
6x - 5 + 5 = 4 + 5 → 6x = 9
Et maintenant, nous résolvons le "x" inconnu:
x = 9/6 = 3/2
Ce qui équivaut à diviser les deux côtés de l'égalité par 6. Nous pouvons donc utiliser ce qui suit pour obtenir la solution:
-La même quantité peut être ajoutée ou soustraite des deux côtés de l'égalité dans une équation, sans la modifier.
-Vous pouvez également multiplier (ou diviser) par le même montant tous les termes à gauche et à droite de l'équation.
-Et si les deux membres d'une équation sont élevés à la même puissance, l'égalité n'est pas modifiée non plus.
Index des articles
La solution d'une équation du premier degré est également connue sous le nom de sa racine. C'est la valeur de x qui convertit l'expression d'origine en une égalité. Par exemple dans:
5x = 8x - 15
Si nous substituons x = 5 dans cette équation, nous obtenons:
5⋅5 = 8⋅5 - 15
25 = 40 - 15
25 = 25
Étant donné que les équations linéaires du premier degré se présentent sous de nombreuses formes, qui ne sont parfois pas évidentes, il existe une série de règles générales qui incluent diverses manipulations algébriques, afin de trouver la valeur de l'inconnu:
-Tout d'abord, s'il y a des opérations indiquées, elles doivent être effectuées.
-Les symboles de regroupement tels que les parenthèses, les crochets et les accolades, le cas échéant, doivent être supprimés en conservant les signes appropriés.
-Les termes sont transposés pour placer tous ceux qui contiennent l'inconnu d'un côté de l'égalité, et ceux qui ne le contiennent pas de l'autre.
-Ensuite, tous les termes similaires sont réduits pour arriver à la forme ax = -b.
-Et la dernière étape consiste à effacer l'inconnu.
L'équation du premier degré soulevée au début peut être dérivée de l'équation de la ligne y = mx + c, faisant y = 0. La valeur résultante de x correspond à l'intersection de la ligne avec l'axe horizontal.
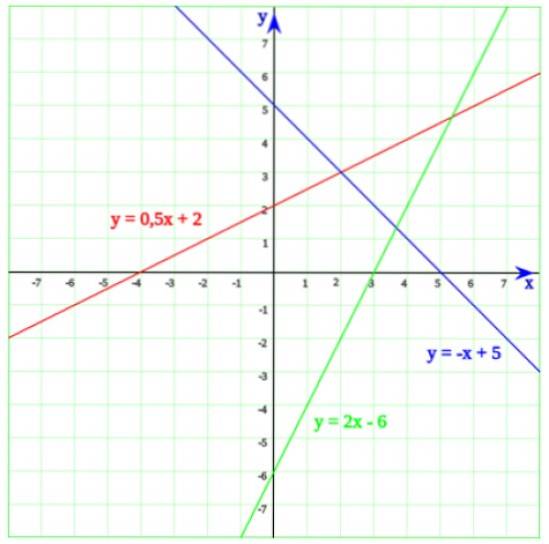
Dans la figure suivante, il y a trois lignes. En commençant par la ligne verte, dont l'équation est:
y = 2x - 6
En faisant y = 0 dans l'équation de la droite, l'équation du premier degré est obtenue:
2x - 6 = 0
Dont la solution est x = 6/2 = 3. Maintenant, quand on détaille le graphique, il est facile de se rendre compte qu'en effet, la ligne coupe l'axe horizontal à x = 3.
La ligne bleue coupe l'axe des x à x = 5, qui est la solution de l'équation -x + 5 = 0. Enfin, la ligne dont l'équation est y = 0,5x + 2 coupe l'axe des x à x = - 4 , qui se voit facilement à partir de l'équation du premier degré:
0,5 x + 2 = 0
x = 2 / 0,5 = 4
Ce sont ceux aux termes desquels il n'y a pas de dénominateurs, par exemple:
21 - 6x = 27 - 8x
Votre solution est:
-6x + 8x = 27 - 21
2x = 6
x = 3
Ces équations contiennent au moins un dénominateur autre que 1. Pour les résoudre, il convient de multiplier tous les termes par le plus petit commun multiple (LCM) des dénominateurs, afin de les éliminer.
L'équation suivante est de type fractionnaire:
Comme ces nombres sont petits, il n'est pas difficile de voir que m.c.m (6, 8,12) = 24. Ce résultat est facilement obtenu en exprimant les nombres comme un produit de nombres premiers ou de leurs puissances, voyons:
6 = 3,2
8 = 23
12 = 2deux⋅3
Le plus petit commun multiple est déterminé en multipliant les facteurs communs et rares de 6, 8 et 12 par leur plus grand exposant, puis:
ppcm (6,8,12) = 23 ⋅3 = 8 × 3 = 24
Puisque nous avons le plus petit multiple commun, il doit être multiplié par chacun des termes de l'équation:
4 (x + 5) -3 (2x + 3) = 2 (1-5x)
Nous utilisons la propriété distributive:
4x + 20 - 6x -9 = 2 - 10x
Tous les termes qui contiennent le "x" inconnu sont regroupés sur le côté gauche de l'égalité, laissant les termes indépendants ou numériques sur le côté droit:
4x - 6x + 10 x = 2 +9 - 20
8x = -9
x = - 9/8
Ce sont des équations linéaires à une inconnue, qui sont cependant accompagnées de coefficients littéraux (lettres). Ces lettres sont traitées de la même manière que les nombres. Un exemple d'équation littérale du premier degré est:
-3ax + 2a = 5x - b
Cette équation est résolue de la même manière que si les termes et coefficients indépendants étaient numériques:
-3ax - 5x = - b - 2a
Factorisation du "x" inconnu:
x (-3a - 5) = - b - 2a
x = (- b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)
Les systèmes d'équations consistent en un ensemble d'équations avec au moins deux inconnues. La solution du système consiste en des valeurs qui satisfont les équations simultanément et pour la déterminer sans équivoque, il doit y avoir une équation pour chaque inconnue.
La forme générale d'un système de m équations linéaires avec n unknowns est:
àOnzeX1 + à12Xdeux +… à1nXn = b1
àvingt-et-unX1 + à22Xdeux +… à2nXn = bdeux
...
àm1X1 + àm2Xdeux +… àmnXn = bm
Si le système a une solution, on dit qu'il est compatible déterminé, quand il y a un ensemble infini de valeurs qui le satisfont est compatible indéterminé, et enfin s'il n'a pas de solution alors c'est incompatible.
Dans la résolution de systèmes d'équations linéaires, plusieurs méthodes sont utilisées: la réduction, la substitution, l'égalisation, les méthodes graphiques, l'élimination de Gauss-Jordan et l'utilisation de déterminants sont parmi les plus utilisées. Mais il existe d'autres algorithmes pour arriver à la solution, plus pratique pour les systèmes avec de nombreuses équations et inconnues.
Un exemple de système d'équations linéaires à deux inconnues est:
8x - 5 = 7y - 9
6x = 3y + 6
La solution de ce système est présentée plus loin dans la section des exercices résolus..
La valeur absolue d'un nombre réel est la distance entre son emplacement sur la droite numérique et 0 sur la droite numérique. Comme il s'agit d'une distance, sa valeur est toujours positive.
La valeur absolue d'un nombre est indiquée par les barres modulo: │x│. La valeur absolue d'un nombre positif ou négatif est toujours positive, par exemple:
│ + 8│ = 8
│-3│ = 3
Dans une équation de valeur absolue, l'inconnue se situe entre les barres de module. Considérons l'équation simple suivante:
│x│ = 10
Il y a deux possibilités, la première est que x est un nombre positif, auquel cas nous avons:
x = 10
Et l'autre possibilité est que x soit un nombre négatif, dans ce cas:
x = -10
Telles sont les solutions de cette équation. Regardons maintenant un exemple différent:
│x + 6│ = 11
Le montant à l'intérieur des barres peut être positif, donc:
x + 6 = 11
x = 11 -6 = 5
Ou cela peut être négatif. Dans ce cas:
-(x + 6) = 11
-x - 6 = 11 ⇒ -x = 11 + 6 = 17
Et la valeur de l'inconnu est:
x = -17
Cette équation de valeur absolue a donc deux solutions: x1 = 5 et xdeux = -17. Nous pouvons vérifier que les deux solutions conduisent à une égalité dans l'équation d'origine:
│5 + 6│ = 11
│11│ = 11
Oui
│-17 + 6│ = 11
│-11│ = 11
Résolvez le système d'équations linéaires suivant avec deux inconnues:
8x - 5 = 7y -9
6x = 3y + 6
Tel qu'il est proposé, ce système est idéal pour utiliser la méthode de substitution, puisque dans la deuxième équation l'inconnue X est presque prêt pour le dédouanement:
x = (3y + 6) / 6
Et il peut être immédiatement substitué dans la première équation, qui devient alors une équation du premier degré avec un "y" inconnu:
8 [(3y + 6) / 6] - 5 = 7y - 9
Le dénominateur peut être supprimé en multipliant chaque terme par 6:
6. 8⋅ [(3y + 6) / 6] - 6,5 = 6 .7y- 6. 9
8⋅ (3 ans + 6) - 30 = 42 ans - 54
Application de la propriété distributive dans le premier terme à droite de l'égalité:
24y + 48-30 = 42y - 54 ⇒ 24y + 18 = 42y - 54
L'équation peut être simplifiée, puisque tous les coefficients sont des multiples de 6:
4 ans + 3 = 7 ans - 9
-3y = -12
y = 4
Avec ce résultat, nous allons à la compensation de x:
x = (3y +6) / 6 → x = (12 + 6) / 6 = 3
Résolvez l'équation suivante:
Les produits apparaissent dans cette équation, et en suivant les instructions données au début, ils doivent d'abord être développés:
3x - 10x +14 = 5x + 36x + 12
Ensuite, tous les termes qui contiennent les inconnues sont placés du côté gauche de l'égalité, et du côté droit seront les termes indépendants:
3x - 10x - 5x - 36x = 12 - 14
-48x = -2
x = 1/24
L'ajout des trois angles intérieurs d'un triangle donne 180 °. Le majeur dépasse le mineur de 35 °, et ce dernier dépasse à son tour de 20 ° la différence entre le majeur et le médium. Quels sont les angles?
Nous appellerons «x» le plus grand angle, «y» le milieu et «z» le plus petit. Lorsque la déclaration affirme que la somme d'entre eux est de 180 °, il peut s'écrire:
x + y + z = 180
Alors on sait que le plus grand dépasse le moindre de 35 °, on peut écrire ceci comme ceci:
x = z + 35
Enfin, le plus petit dépasse la différence entre le plus grand et le milieu de 20 °:
z = x - y + 20
Nous avons un système de 3 équations et 3 inconnues:
x + y + z = 180
x = z + 35
z = x - y + 20
En résolvant z à partir de la première équation, nous avons:
z = 180 - x - y
Correspondance avec le troisième:
180 - x - y = x - y + 20
Passer les inconnues sur le côté gauche comme toujours:
-x - y - x + y = 20 - 180
Le "y" est annulé et reste:
-2x = - 160
x = 80 °
À partir de la deuxième équation, nous trouvons la valeur de z:
z = x - 35 = 80 - 35 = 45 °
Et la valeur de y se trouve à partir du premier ou du troisième:
y = 180 - x - z = 180 - 80 - 45 = 55º
Personne n'a encore commenté ce post.