le équations polynomiales Il s'agit d'une déclaration qui élève l'égalité de deux expressions ou membres, où au moins un des termes qui composent chaque côté de l'égalité sont des polynômes P (x). Ces équations sont nommées en fonction du degré de leurs variables.
En général, une équation est une déclaration qui établit l'égalité de deux expressions, où dans au moins une de celles-ci il y a des quantités inconnues, appelées variables ou inconnues. Bien qu'il existe de nombreux types d'équations, elles sont généralement classées en deux types: algébrique et transcendantale..
Les équations polynomiales contiennent uniquement des expressions algébriques, qui peuvent avoir une ou plusieurs inconnues impliquées dans l'équation. Selon l'exposant (degré) qu'ils ont, ils peuvent être classés en: premier degré (linéaire), deuxième degré (quadratique), troisième degré (cubique), quatrième degré (quartique), degré supérieur ou égal à cinq et irrationnel.
Index des articles
Les équations polynomiales sont des expressions formées par une égalité entre deux polynômes; c'est-à-dire par les sommes finies de multiplications entre des valeurs inconnues (variables) et des nombres fixes (coefficients), où les variables peuvent avoir des exposants, et leur valeur peut être un entier positif, y compris zéro.
Les exposants déterminent le degré ou le type d'équation. Le terme de l'expression qui a l'exposant de valeur la plus élevée représentera le degré absolu du polynôme.
Les équations polynomiales sont également appelées algébriques, leurs coefficients peuvent être des nombres réels ou complexes et les variables sont des nombres inconnus représentés par une lettre, tels que: "x".
Si en substituant une valeur à la variable "x" dans P (x), le résultat est égal à zéro (0), alors cette valeur est dite satisfaire l'équation (c'est une solution), et est généralement appelée la racine du polynôme.
Lors du développement d'une équation polynomiale, vous voulez trouver toutes les racines ou solutions.
Il existe plusieurs types d'équations polynomiales, qui se différencient selon le nombre de variables, mais aussi selon le degré de leur exposant.
Ainsi, les équations polynomiales -où son premier terme est un polynôme qui a une seule inconnue, considérant que son degré peut être n'importe quel nombre naturel (n) et le second terme est zéro-, peuvent être exprimées comme suit:
àn * Xn + àn-1 * Xn-1 +… + A1 * X1 + à0 * X0 = 0
Où:
- àn, àn-1 déjà0, sont des coefficients réels (nombres).
- àn est différent de zéro.
- L'exposant n est un entier positif qui représente le degré de l'équation.
- x est la variable ou inconnue à rechercher.
Le degré absolu ou supérieur d'une équation polynomiale est l'exposant ayant la valeur la plus élevée parmi tous ceux qui forment le polynôme; ainsi, les équations sont classées comme suit:
Les équations polynomiales du premier degré, également appelées équations linéaires, sont celles dans lesquelles le degré (le plus grand exposant) est égal à 1, le polynôme est de la forme P (x) = 0; et il est composé d'un terme linéaire et d'un terme indépendant. Il s'écrit comme suit:
hache + b = 0.
Où:
- a et b sont des nombres réels et a ≠ 0.
- ax est le terme linéaire.
- b est le terme indépendant.
Par exemple, l'équation 13x - 18 = 4x.
Pour résoudre des équations linéaires, tous les termes qui contiennent l'inconnu x doivent être passés d'un côté de l'égalité, et ceux qui n'en ont pas se déplacent de l'autre côté, afin de le résoudre et d'obtenir une solution:
13x - 18 = 4x
13x = 4x + 18
13x - 4x = 18
9x = 18
x = 18 ÷ 9
x = 2.
Ainsi, l'équation donnée n'a qu'une seule solution ou racine, qui est x = 2.
Les équations polynomiales du deuxième degré, également appelées équations quadratiques, sont celles dans lesquelles le degré (le plus grand exposant) est égal à 2, le polynôme est de la forme P (x) = 0, et est composé d'un terme quadratique, un linéaire et un indépendant. Il s'exprime comme suit:
hachedeux + bx + c = 0.
Où:
- a, b et c sont des nombres réels et a ≠ 0.
- hachedeux est le terme quadratique et "a" est le coefficient du terme quadratique.
- bx est le terme linéaire et "b" est le coefficient du terme linéaire.
- c est le terme indépendant.
Généralement, la solution de ce type d'équations est donnée en résolvant x à partir de l'équation, et c'est comme suit, qui est appelée résolvante:
Là, (bdeux - 4ac) est appelé le discriminant de l'équation et cette expression détermine le nombre de solutions que l'équation peut avoir:
- Oui Bdeux - 4ac) = 0, l'équation aura une solution simple double; c'est-à-dire qu'il aura deux solutions égales.
- Oui Bdeux - 4ac)> 0, l'équation aura deux solutions réelles différentes.
- Oui Bdeux - 4ac) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).
Par exemple, nous avons l'équation 4xdeux + 10x - 6 = 0, pour le résoudre, identifiez d'abord les termes a, b et c, puis remplacez-les dans la formule:
a = 4
b = 10
c = -6.
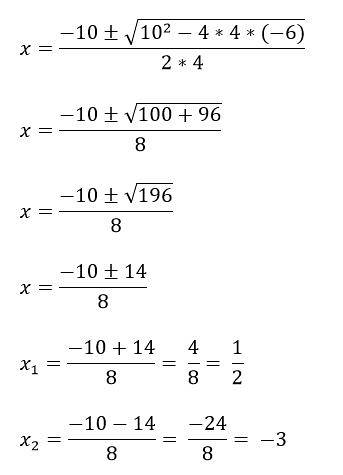
Il y a des cas dans lesquels les équations polynomiales du deuxième degré n'ont pas les trois termes, et c'est pourquoi elles sont résolues d'une manière différente:
- Dans le cas où les équations quadratiques n'ont pas le terme linéaire (c'est-à-dire b = 0), l'équation sera exprimée comme axdeux + c = 0. Pour le résoudre, résolvez pour xdeux et les racines carrées sont appliquées à chaque membre, en se rappelant que les deux signes possibles que l'inconnu peut avoir doivent être considérés:
hachedeux + c = 0.
Xdeux = - c ÷ a
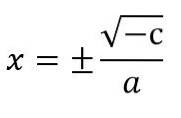
Par exemple, 5 xdeux - 20 = 0.
5 xdeux = 20
Xdeux = 20 ÷ 5
x = ± √4
x = ± 2
X1 = 2.
Xdeux = -2.
- Lorsque l'équation quadratique n'a pas de terme indépendant (c'est-à-dire c = 0), l'équation sera exprimée comme axdeux + bx = 0. Pour le résoudre, il faut prendre le facteur commun de l'inconnu x dans le premier membre; Comme l'équation est égale à zéro, il est vrai qu'au moins un des facteurs sera égal à 0:
hachedeux + bx = 0.
x (ax + b) = 0.
Ainsi, vous devez:
x = 0.
x = -b ÷ a.
Par exemple: nous avons l'équation 5xdeux + 30x = 0. Premier facteur:
5xdeux + 30x = 0
x (5x + 30) = 0.
Deux facteurs sont générés qui sont x et (5x + 30). On considère que l'un de ceux-ci sera égal à zéro et l'autre reçoit une solution:
X1 = 0.
5x + 30 = 0
5x = -30
x = -30 ÷ 5
Xdeux = -6.
Les équations polynomiales de degré supérieur sont celles qui partent du troisième degré, qui peuvent être exprimées ou résolues avec l'équation polynomiale générale pour n'importe quel degré:
àn * Xn + àn-1 * Xn-1 +… + A1 * X1 + à0 * X0 = 0
Ceci est utilisé parce qu'une équation avec un degré supérieur à deux est le résultat de la factorisation d'un polynôme; c'est-à-dire qu'il est exprimé comme la multiplication de polynômes de degré un ou plus, mais sans racines réelles.
La solution de ce type d'équations est directe, car la multiplication de deux facteurs sera égale à zéro si l'un des facteurs est nul (0); Par conséquent, chacune des équations polynomiales trouvées doit être résolue, en fixant chacun de ses facteurs à zéro.
Par exemple, nous avons l'équation du troisième degré (cubique) x3 + Xdeux +4x + 4 = 0. Pour le résoudre, les étapes suivantes doivent être suivies:
- Les termes sont regroupés:
X3 + Xdeux +4x + 4 = 0
(X3 + Xdeux ) + (4x + 4) = 0.
- Les membres sont décomposés pour obtenir le facteur commun de l'inconnu:
Xdeux (x + 1) + 4 (x + 1) = 0
(Xdeux + 4)*(x + 1) = 0.
- De cette manière, deux facteurs sont obtenus, qui doivent être égaux à zéro:
(Xdeux + 4) = 0
(x + 1) = 0.
- On voit que le facteur (xdeux + 4) = 0 n'aura pas de solution réelle, tandis que le facteur (x + 1) = 0 en aura. La solution est donc:
(x + 1) = 0
x = -1.
Résolvez les équations suivantes:
(2xdeux + 5)*(x - 3)*(1 + x) = 0.
Dans ce cas, l'équation est exprimée comme la multiplication de polynômes; c'est-à-dire qu'il est pris en compte. Pour le résoudre, chaque facteur doit être égal à zéro:
- 2xdeux + 5 = 0, n'a pas de solution.
- x - 3 = 0
- x = 3.
- 1 + x = 0
- x = - 1.
Ainsi, l'équation donnée a deux solutions: x = 3 et x = -1.
X4 - 36 = 0.
Un polynôme a été donné, qui peut être réécrit comme une différence de carrés pour arriver à une solution plus rapide. Ainsi, l'équation est:
(Xdeux + 6)*(Xdeux - 6) = 0.
Pour trouver la solution des équations, les deux facteurs sont mis à zéro:
(Xdeux + 6) = 0, n'a pas de solution.
(Xdeux - 6) = 0
Xdeux = 6
x = ± √6.
Ainsi, l'équation initiale a deux solutions:
x = √6.
x = - √6.
Personne n'a encore commenté ce post.