
Equations d'équilibre thermique, applications, exercices
L'équilibre thermique de deux corps qui sont en contact thermique est l'état qui est atteint après un temps suffisamment long pour que les températures des deux corps s'égalisent.
En thermodynamique, le contact thermique de deux corps (ou de deux systèmes thermodynamiques) est compris comme une situation dans laquelle les corps ont un contact mécanique ou sont séparés mais en contact avec une surface qui ne permet que le passage de la chaleur d'un corps à l'autre (diathermique surface).
-

Figure 1. Après un certain temps, la glace et la boisson atteindront leur équilibre thermique. Source: pixabay
En contact thermique, il ne doit y avoir aucune réaction chimique entre les systèmes en contact. Il ne devrait y avoir qu'un échange de chaleur.
Des situations quotidiennes dans lesquelles il y a échange de chaleur se produisent avec des systèmes tels que la boisson froide et le verre, le café chaud et la cuillère à café, ou le corps et le thermomètre, parmi de nombreux autres exemples..
Index des articles
- 1 Quand deux ou plusieurs systèmes sont-ils en équilibre thermique??
- 2 Equations d'équilibre thermique
- 2.1 Température d'équilibre
- 2.2 Contact thermique avec changement de phase
- 3 applications
- 3.1 -Exercice 1
- 4 exercices résolus
- 4.1 -Exercice 2
- 4.2 Exercice 3
- 4.3 -Exercice 4
- 5 Références
Lorsque deux ou plusieurs systèmes sont en équilibre thermique?
La deuxième loi de la thermodynamique stipule que la chaleur va toujours du corps avec la température la plus élevée au corps avec la température la plus basse. Le transfert de chaleur cesse dès que les températures s'égalisent et que l'état d'équilibre thermique est atteint..
L'application pratique de l'équilibre thermique est le thermomètre. Un thermomètre est un appareil qui mesure sa propre température, mais grâce à l'équilibre thermique, nous pouvons connaître la température d'autres corps, comme celle d'une personne ou d'un animal.
Le thermomètre à colonne de mercure est placé en contact thermique avec le corps, par exemple sous la languette, et il faut attendre suffisamment de temps pour que l'équilibre thermique entre le corps et le thermomètre soit atteint et que sa lecture ne varie pas davantage..
Lorsque ce point est atteint, la température du thermomètre est la même que celle du corps.
La loi zéro de la thermodynamique stipule que si un corps A est en équilibre thermique avec un corps C et que ce même corps C est en équilibre thermique avec B, alors A et B sont en équilibre thermique même s'il n'y a pas de contact thermique entre A et B.
Par conséquent, nous concluons que deux ou plusieurs systèmes sont en équilibre thermique lorsqu'ils ont la même température.
Équations d'équilibre thermique
On suppose un corps A de température initiale Ta en contact thermique avec un autre corps B de température initiale Tb. Nous supposons également que Ta> Tb, alors selon la deuxième loi la chaleur est transférée de A à B.
Au bout d'un moment, l'équilibre thermique sera atteint et les deux corps auront la même température finale Tf. Cela aura une valeur intermédiaire à Ta et Tb, c'est-à-dire Ta> Tf> Tb.
La quantité de chaleur Qa transférée de A à B sera Qa = Ma Ca (Tf - Ta), où Ma est la masse du corps A, Ca la capacité calorifique par unité de masse de A et (Tf - Ta) la différence de température. Si Tf est inférieur à Ta alors Qa est négatif, indiquant que le corps A abandonne la chaleur.
De même pour le corps B on a que Qb = Mb Cb (Tf - Tb); et si Tf est supérieur à Tb alors Qb est positif, indiquant que le corps B reçoit de la chaleur. Le corps A et le corps B étant en contact thermique l'un avec l'autre, mais isolés de l'environnement, la quantité totale de chaleur échangée doit être nulle: Qa + Qb = 0
Alors Ma Ca (Tf - Ta) + Mb Cb (Tf - Tb) = 0
Température d'équilibre
En développant cette expression et en résolvant pour la température Tf la température finale d'équilibre thermique est obtenue.
-

Figure 2. Température d'équilibre final. Source: fait soi-même
Tf = (Ma Ca Ta + Mb Cb Tb) / (Ma Ca + Mb Cb).
Dans un cas particulier, considérons le cas où les corps A et B sont identiques en masse et en capacité thermique, dans ce cas la température d'équilibre sera:
Tf = (Ta + Tb) / 2 ↔ si Ma = Mb et Ca = Cb.
Contact thermique avec changement de phase
Dans certaines situations, il arrive que lorsque deux corps sont mis en contact thermique, l'échange thermique provoque le changement d'état ou de phase de l'un d'eux. Si cela se produit, il faut tenir compte du fait que pendant le changement de phase, il n'y a pas de changement de température dans le corps qui modifie son état.
Si le changement de phase de l'un des corps en contact thermique se produit, le concept de chaleur latente L est appliqué, qui est l'énergie par unité de masse nécessaire au changement d'état:
Q = L ∙ M
Par exemple, pour faire fondre 1 kg de glace à 0 ° C 333,5 kJ / kg sont nécessaires et cette valeur est la chaleur latente L de fonte de la glace.
Pendant la fusion, elle passe de l'eau solide à l'eau liquide, mais cette eau maintient la même température que la glace pendant le processus de fusion..
Applications
L'équilibre thermique fait partie de la vie quotidienne. Par exemple, examinons cette situation en détail:
-Exercice 1
Une personne veut se baigner dans de l'eau tiède à 25 ° C. Dans un seau, placez 3 litres d'eau froide à 15 ° C et dans la cuisine chauffez l'eau à 95 ° C.
Combien de litres d'eau chaude devez-vous ajouter au seau d'eau froide pour obtenir la température finale souhaitée?
Solution
Supposons que A est de l'eau froide et B est de l'eau chaude:
-
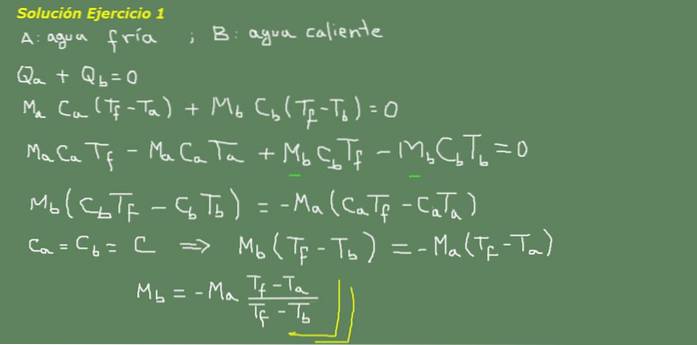
Figure 3. Solution de l'exercice 3. Source: propre élaboration.
Nous proposons l'équation d'équilibre thermique, comme indiqué sur le tableau noir de la figure 3 et à partir de là, nous résolvons pour la masse d'eau Mb.
La masse initiale d'eau froide peut être obtenue car la densité de l'eau est connue, qui est de 1 kg par litre. Autrement dit, nous avons 3 kg d'eau froide.
Ma = 3 kg
Ensuite
Mb = - 3 kg * (25 ° C - 15 ° C) / (25 ° C - 95 ° C) = 0,43 kg
Puis 0,43 litre d'eau chaude suffit pour finalement obtenir 3,43 litres d'eau chaude à 25 ° C.
Exercices résolus
-Exercice 2
Un morceau de métal d'une masse de 150 g et d'une température de 95 ° C est introduit dans un récipient contenant un demi-litre d'eau à une température de 18 ° C. Au bout d'un moment, l'équilibre thermique est atteint et la température de l'eau et du métal est de 25 ° C.
Supposons que le récipient contenant l'eau et le morceau de métal soit un thermos fermé qui ne permet pas l'échange de chaleur avec l'environnement.
Obtenir la chaleur spécifique du métal.
Solution
Nous allons d'abord calculer la chaleur absorbée par l'eau:
Qa = Ma Ca (Tf - Ta)
Qa = 500g 1cal / (g ° C) (25 ° C - 18 ° C) = 3500 calories.
C'est la même chaleur donnée par le métal:
Qm = 150g Cm (25 ° C - 95 ° C) = -3500 calories.
Ainsi, nous pouvons obtenir la capacité thermique du métal:
Cm = 3500 cal / (150g 70 ° C) = ⅓ cal / (g ° C).
Exercice 3
Vous avez 250 c.c. d'eau à 30 ° C A cette eau qui se trouve dans un thermos isolant, on ajoute 25g de glaçons à 0 ° C, dans le but de la refroidir.
Déterminez la température d'équilibre; c'est-à-dire la température qui restera une fois que toute la glace aura fondu et que l'eau glacée se sera réchauffée pour correspondre à celle de l'eau dans le verre initialement.
Solution 3
Cet exercice peut être résolu en trois étapes:
- Le premier est la fonte de la glace qui absorbe la chaleur de l'eau initiale pour fondre et devenir de l'eau..
- Ensuite, la chute de température dans l'eau initiale est calculée, en raison du fait qu'elle a renoncé à la chaleur (Qced<0) para fundir el hielo.
- Enfin, l'eau fondue (provenant de la glace) doit être thermiquement équilibrée avec l'eau qui existait initialement..
-

Figure 4. Solution de l'exercice 3. Source: propre élaboration.
Calculons la chaleur nécessaire à la fonte de la glace:
Qf = L * Mh = 333,5 kJ / kg * 0,025 kg = 8,338 kJ
Ensuite, la chaleur donnée par l'eau pour faire fondre la glace est Qced = -Qf
Cette chaleur dégagée par l'eau abaisse sa température à une valeur T 'que l'on peut calculer comme suit:
T '= T0 - Qf / (Ma * Ca) = 22,02 ° C
Où Ca est la capacité calorifique de l'eau: 4,18 kJ / (kg ° C).
Enfin, la masse d'eau d'origine qui est maintenant à 22,02 ° C cédera de la chaleur à la masse d'eau fondue de la glace qui est à 0 ° C..
Enfin la température d'équilibre Te sera atteinte après un temps suffisant:
Te = (Ma * T '+ Mh * 0 ° C) / (Ma + Mh) = (0,25 kg * 22,02 ° C + 0,025 kg * 0 ° C) / (0,25 kg + 0,025 kg).
Obtention enfin de la température d'équilibre:
Te = 20,02 ° C.
-Exercice 4
Un morceau de plomb de 0,5 kg sort du four à une température de 150 ° C, ce qui est bien en dessous de son point de fusion. Cette pièce est placée dans un récipient contenant 3 litres d'eau à température ambiante de 20 ° C. Déterminer la température d'équilibre finale.
Calculez également:
- Quantité de chaleur fournie par le plomb à l'eau.
- Quantité de chaleur absorbée par l'eau.
Données:
Chaleur spécifique du plomb: Cp = 0,03 cal / (g ° C); chaleur spécifique de l'eau: Ca = 1 cal / (g ° C).
Solution
Nous déterminons d'abord la température d'équilibre finale Te:
Te = (Ma Ca Ta + Mp Cp Tp) / (Ma Ca + Mp Cp)
Te = 20,65 ° C
Ensuite, la quantité de chaleur dégagée par le plomb est:
Qp = Mp Cp (Te - Tp) = -1,94 x 10³ cal.
La quantité de chaleur absorbée par l'eau sera:
Qa = Ma Ca (Te - Ta) = + 1,94x 10³ cal.
Les références
- Atkins, P. 1999. Chimie physique. Éditions Omega.
- Bauer, W. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
- Giancoli, D. 2006. Physique: principes avec applications. 6ème… Ed Prentice Hall.
- Hewitt, Paul. 2012. Science physique conceptuelle. 5ème. Ed. Pearson.
- Resnick, R. (1999). Physique. Vol. 1. 3e éd. En espagnol. Compañía Editorial Continental S.A. par C.V.
- Rex, A. 2011. Fondamentaux de la physique. Pearson.
- Sears, Zemansky. 2016. Physique universitaire et physique moderne. 14e. Éd. Volume 1.
- Serway, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Éd. Cengage Learning.


Personne n'a encore commenté ce post.