
Espace vectoriel de base et dimension, axiomes, propriétés
UNE espace vectoriel est un ensemble non vide V= ou alors, v, w,…, dont les éléments sont des vecteurs. Certaines opérations importantes sont effectuées avec eux, parmi lesquelles se distinguent les suivantes:
- Somme entre deux vecteurs u + v quels résultats z, qui appartient à l'ensemble V.
- Multiplication d'un nombre réel α par un vecteur v: α v ce qui donne un autre vecteur Oui qui appartient à V.

Pour désigner un vecteur, nous utilisons gras (v est un vecteur), et pour les scalaires ou les nombres lettres grecques (α est un nombre).
Index des articles
- 1 Axiomes et propriétés
- 2 Exemples d'espaces vectoriels
- 2.1 Exemple 1
- 2.2 Exemple 2
- 2.3 Exemple 3
- 2.4 Exemple 4
- 3 Base et dimension d'un espace vectoriel
- 3.1 Base
- 3.2 Dimension
- 3.3 Sous-espace vectoriel
- 4 exercices résolus
- 4.1 -Exercice 1
- 4.2 -Exercice 2
- 4.3 -Exercice 3
- 5 Références
Axiomes et propriétés
Pour qu'un espace vectoriel soit donné, les huit axiomes suivants doivent être satisfaits:
1-commutable: ou alors +v = v +ou alors
2-Transitivité: (ou alors + v) + w = ou alors + ( v + w)
3-Existence du vecteur nul 0 tel que 0 + v = v
4-Existence du contraire: l'opposé de v c'est (-v) , car v + (-v) = 0
5-Distributivité du produit par rapport à la somme vectorielle: α ( ou alors + v ) = αou alors +αv
6-Distributivité du produit par rapport à la somme scalaire: (α + β)v = αv +βv
7-Associativité du produit scalaire: α (β v) = (α β)v
8-Le nombre 1 est l'élément neutre puisque: 1v = v
Exemples d'espaces vectoriels
Exemple 1
Les vecteurs dans le plan (R²) sont un exemple d'espace vectoriel. Un vecteur dans le plan est un objet géométrique qui a à la fois une magnitude et une direction. Il est représenté par un segment orienté appartenant audit plan et de taille proportionnelle à sa grandeur.
La somme de deux vecteurs dans le plan peut être définie comme l'opération de translation géométrique du deuxième vecteur après le premier. Le résultat de la somme est le segment orienté qui part de l'origine du premier et atteint la pointe du second.
Sur la figure on peut voir que la somme dans R² est commutative.
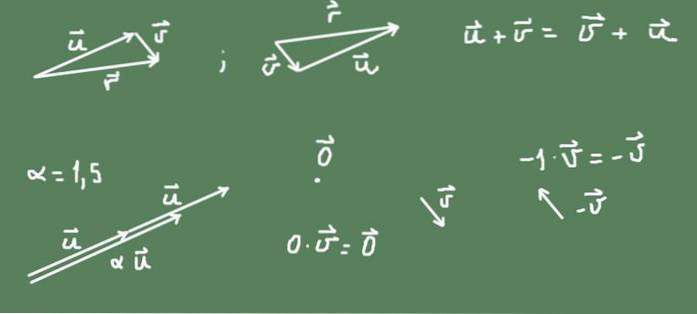
Le produit d'un nombre α et d'un vecteur est également défini. Si le nombre est positif, la direction du vecteur d'origine est conservée et la taille est α fois le vecteur d'origine. Si le nombre est négatif, la direction est opposée et la taille du vecteur résultant est la valeur absolue du nombre.
Le vecteur opposé à n'importe quel vecteur v c'est -v = (- 1) v.
Le vecteur nul est un point dans le plan R², et le nombre zéro fois un vecteur donne le vecteur nul.
Tout ce qui est dit est illustré sur la figure 2.
Exemple 2
Ensemble P de tous les polynômes de degré inférieur ou égal à deux, y compris le degré zéro, forment un ensemble qui satisfait tous les axiomes d'un espace vectoriel.
Soit le polynôme P (x) = a x² + b x + c et Q (x) = d x² + e x + f
La somme de deux polynômes est définie: P (x) + Q (x) = (a + d) x² + (b + e) x + (c + f)
La somme des polynômes appartenant à l'ensemble P est commutative et transitive.
Le polynôme nul appartenant à l'ensemble P est celui dont tous ses coefficients sont égaux à zéro:
0 (x) = 0 x² + 0 x + 0
La somme d'un scalaire α par un polynôme est définie comme suit: α P (x) = α ∙ a x² + α ∙ b x + α ∙ c
Le polynôme opposé de P (x) est -P (x) = (-1) P (x).
De tout ce qui précède, il s'ensuit que l'ensemble P de tous les polynômes de degré inférieur ou égal à deux, est un espace vectoriel.
Exemple 3
Ensemble M de toutes les matrices de m lignes x n colonnes dont les éléments sont des nombres réels forment un espace vectoriel réel, par rapport aux opérations d'addition de matrices et produit d'un nombre par une matrice.
Exemple 4
L'ensemble F de fonctions continues de variable réelle, forme un espace vectoriel, puisqu'il est possible de définir la somme de deux fonctions, la multiplication d'un scalaire par une fonction, la fonction nulle et la fonction symétrique. Ils remplissent également les axiomes qui caractérisent un espace vectoriel.
Base et dimension d'un espace vectoriel
Base
La base d'un espace vectoriel est définie comme un ensemble de vecteurs linéairement indépendants tels qu'à partir d'une combinaison linéaire de ceux-ci, tout vecteur de cet espace vectoriel peut être généré.
La combinaison linéaire de deux vecteurs ou plus consiste à multiplier les vecteurs par un scalaire puis à les ajouter de manière vectorielle.
Par exemple, dans l'espace vectoriel des vecteurs en trois dimensions formé par R³, la base canonique définie par les vecteurs unitaires (de grandeur 1) est utilisée je, j, k.
Où je = (1, 0, 0); j = (0, 1, 0); k = (0, 0, 1). Ce sont les vecteurs cartésiens ou canoniques.
Tout vecteur V appartenant à R³ s'écrit V = a je + b j + c k, qui est une combinaison linéaire des vecteurs de base je, j, k. Les scalaires ou nombres a, b, c sont connus comme les composantes cartésiennes de V.
On dit aussi que les vecteurs de base d'un espace vectoriel forment un ensemble générateur de l'espace vectoriel.
Dimension
La dimension d'un espace vectoriel est le nombre cardinal d'une base vectorielle pour cet espace; c'est-à-dire le nombre de vecteurs qui composent ladite base.
Ce cardinal est le nombre maximum de vecteurs linéairement indépendants de cet espace vectoriel, et en même temps le nombre minimum de vecteurs qui forment un groupe électrogène de cet espace.
Les bases d'un espace vectoriel ne sont pas uniques, mais toutes les bases d'un même espace vectoriel ont la même dimension.
Sous-espace vectoriel
Un sous-espace vectoriel S d'un espace vectoriel V est un sous-ensemble de V dans lequel les mêmes opérations sont définies que dans V et remplit tous les axiomes de l'espace vectoriel. Par conséquent, le sous-espace S sera également un espace vectoriel.
Les vecteurs appartenant au plan XY sont un exemple de sous-espace vectoriel. Ce sous-espace est un sous-ensemble d'un espace vectoriel de dimensionnalité supérieur à l'ensemble des vecteurs appartenant à l'espace tridimensionnel XYZ.
Un autre exemple de sous-espace vectoriel S1 de l'espace vectoriel S formé par toutes les matrices 2 × 2 avec des éléments réels est défini ci-dessous:
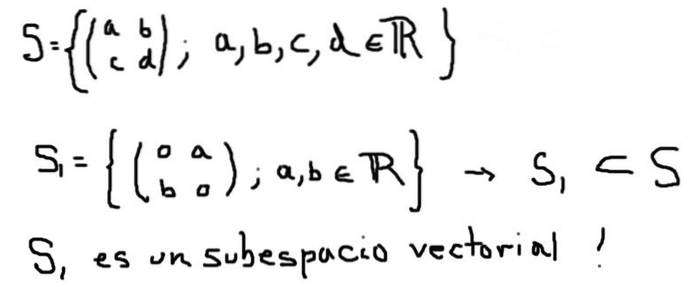
En revanche, S2 défini ci-dessous, bien qu'il s'agisse d'un sous-ensemble de S, ne forme pas un sous-espace vectoriel:

Exercices résolus
-Exercice 1
Que les vecteurs soient V1= (1, 1, 0); V2= (0, 2, 1) et V3= (0, 0, 3) en R³.
a) Montrer qu'ils sont linéairement indépendants.
b) Montrer qu'ils forment une base dans R³, puisque tout triplet (x, y, z) peut s'écrire comme une combinaison linéaire de V1, V2, V3.
c) Trouvez les composants du triple V = (-3,5,4) à la base V1, V2, V3.
Solution
Le critère pour démontrer l'indépendance linéaire consiste à établir l'ensemble suivant d'équations en α, β et γ
α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)
Dans le cas où la seule solution à ce système est α = β = γ = 0 alors les vecteurs sont linéairement indépendants, sinon ils ne le sont pas.
Pour obtenir les valeurs de α, β et γ nous proposons le système d'équations suivant:
α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0
α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0
α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0
Le premier conduit à α = 0, le second α = -2 ∙ β mais puisque α = 0 alors β = 0. La troisième équation implique que γ = (- 1/3) β, mais puisque β = 0 alors γ = 0.
Réponds à
On en conclut qu'il s'agit d'un ensemble de vecteurs linéairement indépendants dans R³ .
Réponse b
Maintenant écrivons le triple (x, y, z) comme une combinaison linéaire de V1, V2, V3.
(x, y, z) = α V1 + β V2 + γ V3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)
α ∙ 1 + β ∙ 0 + γ ∙ 0 = x
α ∙ 1 + β ∙ 2 + γ ∙ 0 = y
α ∙ 0 + β ∙ 1 + γ ∙ 3 = z
Où avez-vous:
α = x
α + 2 β = y
β + 3 γ = z
Le premier indique α = x, le second β = (y-x) / 2 et le troisième γ = (z- y / 2 + x / 2) / 3. De cette façon, nous avons trouvé les générateurs de α, β et γ de tout triplet de R³
Réponse c
Passons à la recherche des composants du triple V = (-3,5,4) à la base V1, V2, V3.
Nous substituons les valeurs correspondantes dans les expressions trouvées ci-dessus pour les générateurs.
Dans ce cas, nous avons: α = -3; β = (5 - (- 3)) / 2 = 4; γ = (4 5/2 + (- 3) / 2) / 3 = 0
C'est-à-dire:
(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)
Finalement:
V = -3 V1 + 4 V2 + 0 V3
Nous concluons que V1, V2, V3 forment une base dans l'espace vectoriel R³ de dimension 3.
-Exercice 2
Exprimer le polynôme P (t) = t² + 4t -3 comme une combinaison linéaire de P1 (t) = t² -2t + 5, P2 (t) = 2t² -3t et P3 (t) = t + 3.
Solution
P (t) = x P1 (t) + y P2 (t) + z P3 (t)
où les nombres x, y, z doivent être déterminés.
La multiplication et le regroupement de termes de même degré en t donne:
t² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)
Ce qui nous amène au système d'équations suivant:
x + 2y = 1
-2x -3y + z = 4
5x + 3z = -3
Les solutions de ce système d'équations sont:
x = -3, y = 2, z = 4.
C'est-à-dire:
P (t) = -3 P1 (t) + 2 P2 (t) + 4 P3 (t)
-Exercice 3
Montrez que les vecteurs v1= (1, 0, -1, 2); v2= (1, 1, 0, 1) et v3= (2, 1, -1, 1) de R⁴ sont linéairement indépendants.
Solution
Nous combinons linéairement les trois vecteurs v1, v2, v3 et nous demandons que la combinaison ajoute l'élément nul de R⁴
à v1 + b v2 + c v3 = 0
C'est-à-dire,
a (1, 0, -1, 2) + b (1, 1, 0, 1) + c (2, 1, -1, 1) = (0, 0, 0, 0)
Cela nous amène au système d'équations suivant:
a + b + 2 c = 0
b + c = 0
-a - c = 0
2 a + b + c = 0
En soustrayant le premier et le quatrième on a: -a + c = 0 ce qui implique a = c.
Mais si nous regardons la troisième équation, nous avons que a = -c. La seule façon pour a = c = (- c) est que c est 0 et donc a sera également 0.
a = c = 0
Si nous substituons ce résultat dans la première équation, nous concluons que b = 0.
Enfin a = b = c = 0, de sorte que l'on peut conclure que les vecteurs v1, v2 et v3 sont linéairement indépendants.
Les références
- Lipschutz, S. 1993. Algèbre linéaire. Deuxième édition. McGraw-Hill. 167 - 198.


Personne n'a encore commenté ce post.