La fonction constante est celui dans lequel la valeur de y est maintenue constante. En d'autres termes: une fonction constante a toujours la forme f (x) = k, où k est un nombre réel.
Lors de la représentation graphique de la fonction constante dans le système de coordonnées xy, aboutit toujours à une ligne droite parallèle à l'axe horizontal ou à l'axe du X.
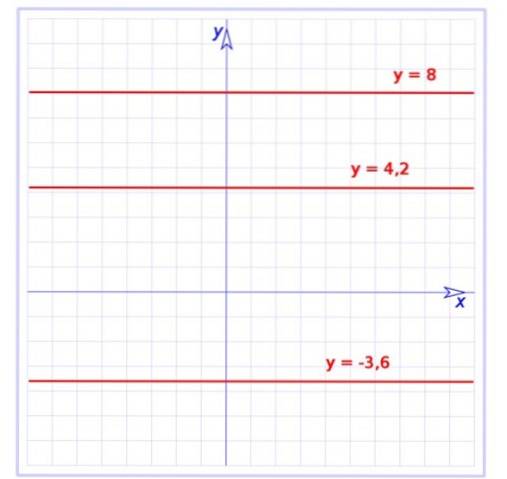
Cette fonction est un cas particulier du fonction affine, dont le graphique est également une ligne droite, mais avec une pente. La fonction constante a une pente nulle, c'est-à-dire qu'il s'agit d'une ligne horizontale, comme le montre la figure 1.
Là, le graphique de trois fonctions constantes est affiché:
f (x) = -3,6
g (x) = 4,2
h (x) = 8
Toutes sont des lignes parallèles à l'axe horizontal, la première d'entre elles est en dessous dudit axe, tandis que les autres sont au-dessus.
Index des articles
Nous pouvons résumer les principales caractéristiques de la fonction constante comme suit:
-Son graphique est une ligne droite horizontale.
-Il a une seule intersection avec l'axe Oui, valeur k.
-Est continu.
-Le domaine de la fonction constante (l'ensemble des valeurs que le X) est l'ensemble des nombres réels R.
-Le chemin, la plage ou le contre-domaine (l'ensemble de valeurs que prend la variable Oui) est simplement la constante k.
Des fonctions sont nécessaires pour établir des liens entre des quantités qui dépendent les unes des autres d'une manière ou d'une autre. La relation entre eux peut être modélisée mathématiquement, pour savoir comment l'un d'eux se comporte lorsque l'autre varie..
Cela aide à construire des modèles pour de nombreuses situations et à faire des prédictions sur leur comportement et leur évolution..
Malgré son apparente simplicité, la fonction constante a de nombreuses applications. Par exemple, lorsqu'il s'agit d'étudier des grandeurs qui restent constantes dans le temps, ou du moins pendant un temps appréciable.
De cette façon, les grandeurs se comportent dans des situations telles que les suivantes:
-La rapidité conduire une voiture sur une longue route droite. Tant que vous ne freinez pas ou n'accélérez pas, la voiture a un mouvement rectiligne uniforme.
-Un condensateur complètement chargé déconnecté d'un circuit a un charge constante dans le temps.
-Enfin, un parking à tarif forfaitaire maintient un le prix constante quelle que soit la durée de stationnement d'une voiture.
La fonction constante peut également être représentée comme suit:
f (x) = kx0
Puisque toute valeur de X élevé à 0 donne 1 comme résultat, l'expression précédente se réduit à l'expression déjà familière:
f (x) = k
Bien sûr, cela se produit tant que la valeur de k est différent de 0.
C'est pourquoi la fonction constante est également classée comme un fonction polynomiale de degré 0, puisque l'exposant de la variable X vaut 0.
Répondre aux questions suivantes:
a) Peut-on affirmer que la droite donnée par x = 4 est une fonction constante? Raison de votre réponse.
b) Une fonction constante peut-elle avoir une intersection?
c) La fonction f (x) = w est-elle constantedeux?
Voici le graphique de la ligne x = 4:
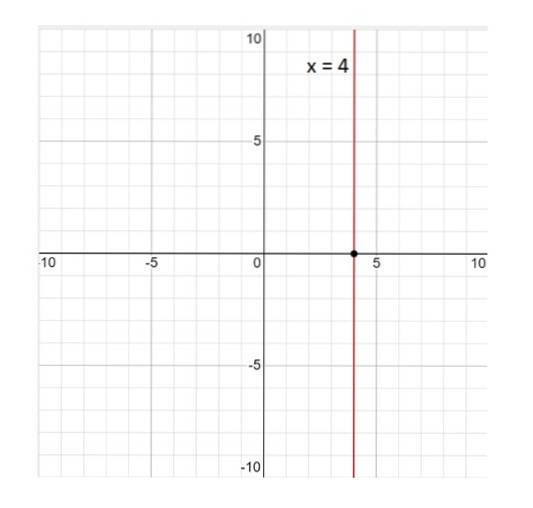
La ligne x = 4 n'est pas une fonction; par définition une fonction est une relation telle qu'à chaque valeur de la variable X correspond à une seule valeur de Oui. Et dans ce cas, ce n'est pas vrai, car la valeur x = 4 est associé à des valeurs infinies de Oui. Par conséquent, la réponse est non.
En général, une fonction constante n'a pas d'intersection avec l'axe X, à moins qu'il ne s'agisse de y = 0, auquel cas c'est l'axe X Bien dit.
Oui, depuis w est constante, de même que son carré. Ce qui compte, c'est que w ne dépend pas de la variable d'entrée X.
Trouvez l'intersection entre les fonctions f (x) = 5 Oui g (x) = 5x - 2
Pour trouver l'intersection entre ces deux fonctions, elles peuvent être respectivement réécrites comme:
y = 5; y = 5x - 2
Ils sont égalisés, obtenant:
5x - 2 = 5
Qu'est-ce qu'une équation linéaire du premier degré, dont la solution est:
5x = 5 + 2 = 7
x = 7/5
Le point d'intersection est (7 / 5,5).
Montrer que la dérivée d'une fonction constante est 0.
De la définition de dérivé, nous avons:
f (x + h) = k
Substituer dans la définition:
Aussi, si nous considérons le dérivé comme le taux de changement dy / dx, la fonction constante ne subit aucun changement, donc sa dérivée est nulle.
Trouvez l'intégrale indéfinie de f (x) = k.
Une compagnie de téléphonie mobile offre un service Internet illimité à forfait pour 15 $ par mois. Quelle est la fonction de prix en fonction du temps?
Soit P le prix à payer en $ et t le temps, qui peut être exprimé en jours. La fonction est définie comme ceci:
P (t) = 15
Le graphique suivant de la vitesse en fonction du temps correspond au mouvement d'une particule.
On demande:
a) Ecrire une expression pour la fonction de vitesse en fonction du temps v (t).
b) Trouvez la distance parcourue par le mobile dans l'intervalle de temps entre 0 et 9 secondes.
D'après le graphique présenté, on peut voir que:
-v = 2 m / s dans l'intervalle de temps entre 0 et 3 secondes
-Le mobile est arrêté entre 3 et 5 secondes, car dans cet intervalle la vitesse est de 0.
-v = - 3 m / s entre 5 et 9 secondes.
C'est un exemple de fonction par morceaux, ou fonction par morceaux, qui à son tour est composée de fonctions constantes, valable uniquement pour les intervalles de temps indiqués. On en conclut que la fonction recherchée est:
À partir du graphique v (t), la distance parcourue par le mobile peut être calculée, ce qui est numériquement équivalent à la surface sous / sur la courbe. De cette manière:
-Distance parcourue entre 0 et 3 secondes = 2 m / s. 3 s = 6 m
-Entre 3 et 5 secondes, il a été arrêté, donc il n'a parcouru aucune distance.
-Distance parcourue entre 5 et 9 secondes = 3 m / s. 4 s = 12 m
Au total, le mobile a parcouru 18 m. Notez que bien que la vitesse soit négative dans l'intervalle entre 5 et 9 secondes, la distance parcourue est positive. Ce qui se passe, c'est que pendant cet intervalle de temps, le mobile avait changé le sens de sa vitesse.
Personne n'a encore commenté ce post.