
Définition de fonction surjective, propriétés, exemples
Ongle fonction surjective est toute relation où chaque élément appartenant au codomaine est une image d'au moins un élément du domaine. Aussi connu sous le nom de fonction sur, font partie de la classification des fonctions en ce qui concerne la manière dont leurs éléments sont liés.
Par exemple une fonction FA → B Défini par F (x) = 2x
Qui lit "F qu'en est-il de À jusqu'à ce que B Défini par F (x) = 2x "
Il est temps de définir les sets de départ et de finition A et B.
R: 1, 2, 3, 4, 5 Maintenant, les valeurs ou images que chacun de ces éléments affichera une fois évalué dans F, seront les éléments du codomaine.
F (1) = 2
F (2) = 4
F (3) = 6
F (4) = 8
F (5) = 10
Formant ainsi le tout B: 2, 4, 6, 8, 10
On peut alors conclure que:
F: 1, 2, 3, 4, 5 → 2, 4, 6, 8, 10 Défini par F (x) = 2x C'est une fonction surjective
Chaque élément du codomaine doit résulter d'au moins une opération de la variable indépendante à travers la fonction en question. Il n'y a pas de limitation des images, un élément du codomaine peut être une image de plus d'un élément du domaine et en essayant toujours un fonction surjective.
L'image montre 2 exemples avec fonctions surjectives.
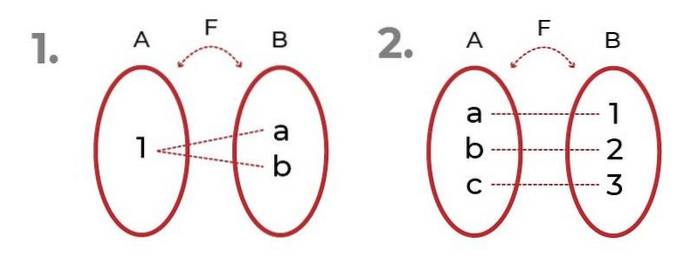
Dans le premier on observe que les images peuvent être référées au même élément, sans compromettre la surjectivité de la fonction.
Dans le second, nous voyons une répartition équitable entre le domaine et les images. Cela donne lieu à fonction bijective, où les critères de fonction injective et fonction surjective.
Une autre méthode d'identification fonctions surjectives, est de vérifier si le codomain est égal à la plage de la fonction. Cela signifie que si l'ensemble d'arrivée est égal aux images fournies par la fonction lors de l'évaluation de la variable indépendante, la fonction est surjective.
Index des articles
- 1 Propriétés
- 1.1 Conditionnement fonctionnel
- 2 Exemples: exercices résolus
- 2.1 Exercice 1
- 2.2 Exercice 2
- 2.3 Exercice 3
- 2.4 Exercice 4
- 2.5 Exercice 4
- 2.6 Exercice 5
- 3 Exercices proposés
- 4 Références
Propriétés
À envisager surjectif à une fonction, les conditions suivantes doivent être remplies:
Être F: DF → CF
∀ b ℮ CF ET à ℮ réF / F (a) = b
C'est la manière algébrique d'établir que pour tout "b" qui appartient à CF il y a un «a» qui appartient à DF tel que la fonction F évaluée en "a" est égale à "b".
La surjectivité est une particularité des fonctions, où le codomaine et la gamme sont similaires. Ainsi, les éléments évalués dans la fonction constituent l'ensemble d'arrivée.
Conditionnement fonctionnel
Parfois une fonction qui n'est pas surjectif, il peut être soumis à certaines conditions. Ces nouvelles conditions peuvent en faire un fonction surjective.
Toutes sortes de modifications du domaine et du codomaine de la fonction sont valides, l'objectif étant de remplir les propriétés de surjectivité dans la relation correspondante.
Exemples: exercices résolus
Pour répondre aux conditions de surjectivité différentes techniques de conditionnement doivent être appliquées, ceci afin de s'assurer que chaque élément du codomaine est dans l'ensemble des images de la fonction.
Exercice 1
- Laissez la fonction F: R → R défini par la ligne F (x) = 8 - x
R: [Tous les nombres réels]
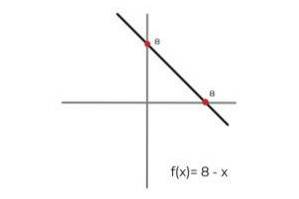
Dans ce cas, la fonction décrit une ligne continue, qui couvre tous les nombres réels dans son domaine et sa plage. Parce que la gamme de la fonction RF égale codomaine R On peut conclure que:
F: R → R défini par la ligne F (x) = 8 - x c'est une fonction surjective.
Ceci s'applique à toutes les fonctions linéaires (Fonctions dont le plus grand degré de la variable est un).
Exercice 2
- Etudiez la fonction F: R → R Défini par F (x) = xdeux : Définissez s'il s'agit d'un fonction surjective. Sinon, montrez les conditions nécessaires pour le rendre surjectif.
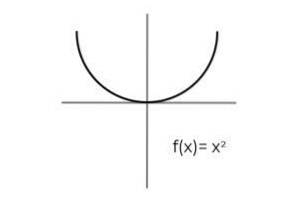
La première chose à considérer est le codomaine de F, qui est composé des nombres réels R. Il n'y a aucun moyen pour la fonction de renvoyer des valeurs négatives, ce qui exclut les vrais négatifs des images possibles.
Conditionnement du codomaine à l'intervalle [0 , ∞ ]. Il est évité de laisser des éléments du codomain sans rapport grâce à F.
Les images sont répétées pour des paires d'éléments de la variable indépendante, telles que x = 1 Oui x = - 1. Mais cela n'affecte que le injectivité de la fonction, ne posant pas de problème pour cette étude.
De cette manière, on peut conclure que:
F: R →[0, ∞ ) Défini par F (x) = xdeux C'est une fonction surjective
Exercice 3
- Définir les conditions du codomaine qu'ils feraient surjectifs aux fonctions
F: R → R Défini par F (x) = Sen (x)
F: R → R Défini par F (x) = Cos (x)
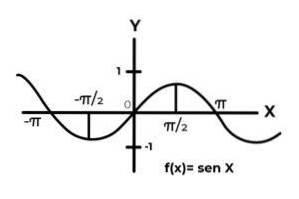
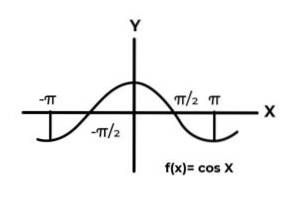
Le comportement des fonctions trigonométriques est similaire à celui des ondes, étant très courant pour trouver des répétitions de la variable dépendante entre les images. Dans la plupart des cas également, la portée de la fonction est limitée à un ou plusieurs secteurs de la ligne réelle.
C'est le cas des fonctions Sinus et Cosinus. Où leurs valeurs fluctuent dans l'intervalle [-1, 1]. Cet intervalle doit conditionner le codomaine pour atteindre la surjectivité de la fonction.
F: R →[ -Onze ] Défini par F (x) = Sen (x) C'est une fonction surjective
F: R →[ -Onze ]Défini par F (x) = Cos (x) C'est une fonction surjective
Exercice 4
- Etudiez la fonction
F: [0, ∞ ) → R Défini par F (x) = ± √x indiquer si c'est un fonction surjective
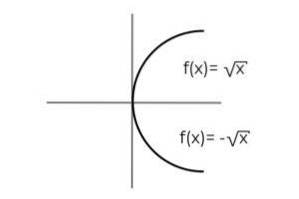
La fonction F (x) = ± √x Il a la particularité de définir 2 variables dépendantes à chaque valeur de "x". Autrement dit, la plage reçoit 2 éléments pour chacun d'entre eux qui est créé dans le domaine. Une valeur positive et négative doit être vérifiée pour chaque valeur de "x".
Lors de l'observation de l'ensemble de départ, on constate que le domaine a déjà été restreint, ceci afin d'éviter les indéterminations produites lors de l'évaluation d'un nombre négatif dans une racine paire.
Lors de la vérification de la plage de la fonction, on note que chaque valeur du codomaine appartient à la plage.
De cette manière, on peut conclure que:
F: [0, ∞ ) → R Défini par F (x) = ± √x C'est une fonction surjective
Exercice 4
- Etudiez la fonction F (x) = Ln x indiquer si c'est un fonction surjective. Conditionner les sets d'arrivée et de départ pour adapter la fonction aux critères de surjectivité.
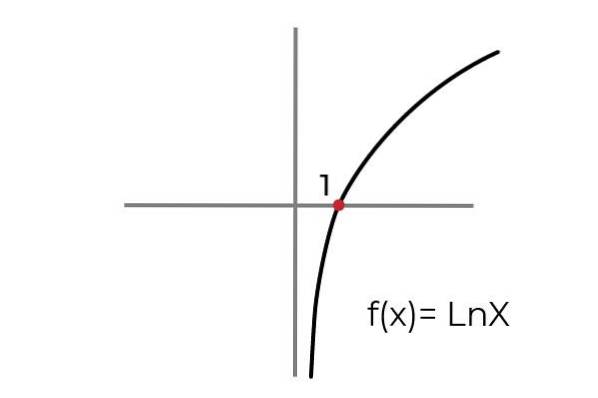
Comme le montre le graphique, la fonction F (x) = Ln xil est défini pour les valeurs de "x" supérieures à zéro. Alors que les valeurs de "et" ou les images peuvent prendre n'importe quelle valeur réelle.
De cette façon, nous pouvons restreindre le domaine de F (x) = à l'intervalle (0 , ∞ )
Tant que la plage de la fonction peut être conservée comme l'ensemble des nombres réels R.
Compte tenu de cela, on peut conclure que:
F: [0, ∞ ) → R Défini par F (x) = Ln x C'est une fonction surjective
Exercice 5
- Etudiez la fonction de valeur absolue F (x) = | x | et désigner les ensembles d'arrivée et de départ qui répondent aux critères de surjectivité.
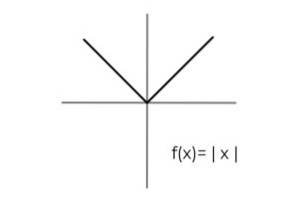
Le domaine de la fonction est valable pour tous les nombres réels R. De cette manière, le seul conditionnement doit être effectué dans le codomaine, en tenant compte du fait que la fonction valeur absolue ne prend que des valeurs positives..
Nous procédons à l'établissement du codomaine de la fonction en l'assimilant au rang de la même
[0 , ∞ )
Maintenant, on peut conclure que:
F: [0, ∞ ) → R Défini par F (x) = | x | C'est une fonction surjective
Exercices proposés
- Vérifiez si les fonctions suivantes sont surjectives:
- F: (0, ∞ ) → R Défini par F (x) = Journal (x + 1)
- F: R → R Défini par F (x) = x3
- F: R →[1, ∞ ) Défini par F (x) = xdeux + 1
- [0, ∞ ) → R Défini par F (x) = Journal (2x + 3)
- F: R → R Défini par F (x) = Sec x
- F: R - 0 → R Défini par F (x) = 1 / x
Les références
- Introduction à la logique et à la pensée critique. Merrilee H. Salmon. Université de Pittsburgh
- Problèmes en analyse mathématique. Piotr Biler, Alfred Witkowski. Université de Wroclaw. Pologne.
- Éléments d'analyse abstraite. Mícheál O'Searcoid PhD. Département de mathématiques. Collège universitaire de Dublin, Beldfield, Dublind 4
- Introduction à la logique et à la méthodologie des sciences déductives. Alfred Tarski, New York Oxford. Presse de l'Université d'Oxford.
- Principes de l'analyse mathématique. Enrique Linés Escardó. Editorial Reverté S. A 1991. Barcelone Espagne.


Personne n'a encore commenté ce post.