
Modèle de gaz parfait, comportement, exemples
UNE gaz parfait ou alors gaz parfait C'est celui dans lequel l'attraction moléculaire ou la force de répulsion entre les particules qui le composent est considérée comme insignifiante, par conséquent, toute son énergie interne est cinétique, c'est-à-dire l'énergie associée au mouvement..
Dans un tel gaz, les particules sont généralement assez éloignées les unes des autres, bien qu'elles se heurtent de temps en temps entre elles et avec les parois du récipient..
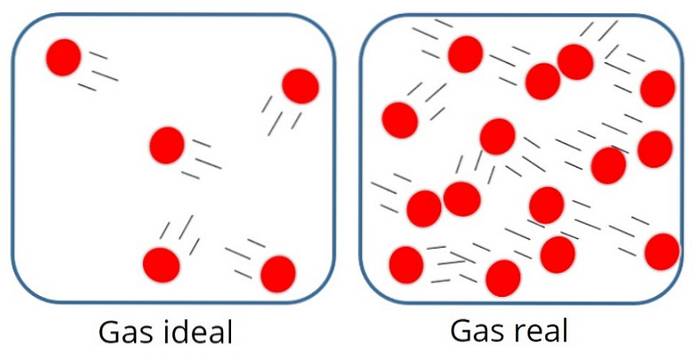
En revanche, dans le gaz parfait, ni la taille ni la masse des particules n'importent, car on suppose que le volume qu'elles occupent est très faible par rapport au volume du gaz lui-même..
Ceci, bien sûr, n'est qu'une approximation, car en réalité, il y a toujours un certain degré d'interaction entre les atomes et les molécules. Nous savons également que les particules occupent de l'espace et ont une masse..
Cependant, ces hypothèses fonctionnent assez bien dans de nombreux cas, tels que les gaz de faible poids moléculaire, dans une bonne plage de pressions et de températures..
Cependant, les gaz de poids moléculaire élevé, en particulier à haute pression ou à basse température, ne se comportent pas du tout comme des gaz idéaux et d'autres modèles créés dans le but de les décrire avec plus de précision sont nécessaires..
Index des articles
- 1 Premières expériences
- 1.1 Les lois des gaz parfaits
- 2 Modèle à gaz parfait
- 2.1 Équation d'état des gaz parfaits
- 2.2 La constante des gaz
- 3 Comportement d'un gaz parfait
- 4 Exemples de gaz parfaits
- 4.1 Gaz nobles
- 4.2 La montgolfière
- 4.3 Ballons à l'hélium
- 5 Références
Premières expériences
Les lois qui régissent les gaz sont empiriques, c'est-à-dire qu'elles sont issues de l'expérimentation. Les expériences les plus notables ont été menées tout au long des XVIIe, XVIIIe et début XIXe siècles.
Les premiers sont ceux de Robert Boyle (1627-1691) et Edme Mariotte (1620-1684), qui ont indépendamment modifié le Pression dans un gaz et a enregistré son changement de le volume, constatant qu'elles étaient inversement proportionnelles: plus la pression est élevée, plus le volume est petit.

De son côté, Jacques Charles (1746-1823) a établi que le volume et Température les valeurs absolues étaient directement proportionnelles, tant que la pression restait constante.
Amadeo Avogadro (1776-1856) a découvert que deux volumes identiques de gaz différents contenaient le même nombre de particules, à condition que la pression et la température soient les mêmes. Et enfin Joseph de Gay Lussac (1778-1850), a déclaré qu'en gardant le volume fixe, la pression dans un gaz est directement proportionnelle à la température..
Les lois des gaz parfaits
Ces découvertes s'expriment dans des formules simples, appelant p à la pression, V au volume, n au nombre de particules et T la température idéale du gaz:
Loi Boyle-Mariotte
Tant que la température est fixe, ce qui suit se produit:
p⋅V = constante
Charles Law
Lorsque le gaz est sous pression constante:
V / T = constante
Loi de Gay Lussac
En maintenant le gaz à un volume fixe, il est satisfait que:
p / T = constante
Loi d'Avogadro
Des volumes de gaz identiques, dans les mêmes conditions de pression et de température, ont le même nombre de particules. On peut donc écrire:
V ∝ n
Où n est le nombre de particules et ∝ est le symbole de proportionnalité.
Modèle de gaz parfait
Le modèle de gaz parfait décrit un gaz tel que:
-Lorsque les particules interagissent, elles le font pendant un temps très court, au moyen de collisions élastiques, dans lesquelles l'impulsion et l'énergie cinétique sont conservées..
-Ses particules constitutives sont ponctuelles, c'est-à-dire que leur diamètre est bien inférieur à la distance moyenne qu'elles parcourent entre une collision et une autre..
-Les forces intermoléculaires sont inexistantes.
-L'énergie cinétique est proportionnelle à la température.
Gases monoatómicos -cuyos átomos no están ligados entre sí- y de bajo peso molecular, en condiciones estándar de presión y temperatura (presión atmosférica y 0 º C de temperatura), tienen un comportamiento tal que el modelo de gas ideal es una muy buena descripción pour eux.
Équation d'état des gaz parfaits
Les lois des gaz énumérées ci-dessus se combinent pour former l'équation générale qui régit le comportement du gaz parfait:
V ∝ n
V ∝ T
Donc:
V ∝ n⋅T
Aussi, d'après la loi de Boyle:
V = constante / p
Nous pouvons donc affirmer que:
V = (constante x n⋅T) / p
La constante s'appelle le constante de gaz et est notée par la lettre R. Avec ce choix, l'équation d'état du gaz parfait met en relation quatre variables qui décrivent l'état du gaz, à savoir n, R, p et T, laissant:
p⋅V = n⋅R⋅T
Cette équation relativement simple est conforme aux lois des gaz parfaits. Par exemple, si la température est constante, l'équation se réduit à la loi de Boyle-Mariotte.
La constante des gaz
Comme nous l'avons déjà dit, dans des conditions standard de température et de pression, c'est-à-dire à 0 ° C (273,15 K) et 1 atmosphère de pression, le comportement de nombreux gaz est proche de celui du gaz idéal. Dans ces conditions, le volume de 1 mole de gaz est de 22414 L.
Dans ce cas:
R = (p⋅V) / (n⋅T) = (1 atm x 22,414 L) / (1 mol x 273,15 K) = 0,0821 atm ⋅ L / mol ⋅ K
La constante de gaz peut également être exprimée en d'autres unités, par exemple dans le système international SI cela vaut:
R = 8,314 J⋅ mol-1⋅ K-1
Lors de la résolution d'un problème en utilisant la loi des gaz parfaits, il convient de prêter attention aux unités dans lesquelles la constante est exprimée, car comme nous pouvons le voir, il existe de nombreuses possibilités.
Comportement d'un gaz parfait
Comme nous l'avons dit, tout gaz dans des conditions standard de pression et de température et qui est de faible poids moléculaire, se comporte très près du gaz idéal. Par conséquent, l'équation p⋅V = n⋅R⋅T est applicable pour trouver la relation entre les quatre variables qui la décrivent: n, p, V et T.
On peut ainsi imaginer une portion de gaz idéal enfermée dans un conteneur et formée de minuscules particules, qui de temps en temps se heurtent entre elles et avec les parois du conteneur, toujours élastiquement..
C'est ce que nous voyons dans l'animation suivante d'une portion d'hélium, un gaz rare monatomique:
Exemples de gaz parfaits
Un gaz parfait est un gaz hypothétique, c'est-à-dire qu'il s'agit d'une idéalisation, cependant, en pratique, de nombreux gaz se comportent de manière très proche, ce qui permet au modèle p⋅V = n⋅R arroT de donner de très bons résultats..
gaz nobles
Des exemples de gaz qui se comportent de manière idéale dans des conditions standard sont les gaz rares, ainsi que les gaz légers: l'hydrogène, l'oxygène et l'azote..
Le ballon aérostatique

La loi de Charles peut être appliquée au ballon à air chaud dans la figure 1: le gaz se réchauffe, donc l'air qui remplit le ballon se dilate et par conséquent monte.
Ballons à l'hélium
L'hélium est, avec l'hydrogène, l'élément le plus commun dans l'univers, et pourtant il est rare sur Terre. Comme il s'agit d'un gaz rare, il est inerte, contrairement à l'hydrogène, c'est pourquoi les ballons remplis d'hélium sont largement utilisés comme éléments décoratifs..
Les références
- Atkins, P. 1999. Chimie physique. Éditions Omega.
- Chang, R. 2013. Chimie. 11ème. Édition. Éducation Mc Graw Hill.
- Cengel, Y. 2012. Thermodynamique. 7e édition. Mcgraw Hill.
- Cimbala, C. 2006. Mécanique des fluides, principes fondamentaux et applications. Mc. Colline de Graw.
- Giambattista, A. 2010. Physique. 2ème. Ed. McGraw Hill.

Personne n'a encore commenté ce post.