le degré d'un polynôme au ongle variable est donnée par le terme qui a le plus grand exposant, et si le polynôme a deux variables ou plus, alors le degré est déterminé par la somme des exposants de chaque terme, la plus grande somme étant le degré du polynôme.
Voyons comment déterminer le degré du polynôme de manière pratique.
Supposons que le polynôme P (x) = -5x + 8x3 + 7 - 4xdeux. Ce polynôme est une variable, dans ce cas c'est la variable X. Ce polynôme se compose de plusieurs termes, qui sont les suivants:
-5x; 8x3; 7; - 4xdeux
Choisissons parmi les quatre termes celui dont l'exposant est le plus grand, ce terme est:
8x3
Et maintenant quel est l'exposant? La réponse est 3. Par conséquent P (x) est un polynôme de degré 3.
Si le polynôme en question a plus d'une variable, alors le degré peut être:
-Absolu
-Par rapport à une variable
Le degré absolu se trouve comme expliqué au début: addition des exposants de chaque terme et sélection du plus grand.
En revanche, le degré du polynôme par rapport à l'une des variables ou lettres est la plus grande valeur de l'exposant que possède ladite lettre. Le point deviendra plus clair avec les exemples et les exercices résolus dans les sections suivantes.
Index des articles
Les polynômes peuvent être classés par degré, et peuvent être du premier degré, du deuxième degré, du troisième degré, etc. Pour l'exemple de la figure 1, l'énergie est un monôme du premier degré pour la masse.
Il est également important de noter que le nombre de termes que possède un polynôme est égal à grade plus 1. A) Oui:
-Les polynômes du premier degré ont 2 termes: a1x + aou alors
-Le polynôme du deuxième degré a 3 termes: adeuxXdeux + à1x + aou alors
-Un polynôme du troisième degré a 4 termes: a3X3 + àdeuxXdeux + à1x + aou alors
Et ainsi de suite. Le lecteur attentif aura remarqué que les polynômes des exemples précédents sont écrits sous la forme décroissant, c'est-à-dire en plaçant le terme en premier avec le Le niveau le plus élevé.
Le tableau suivant montre divers polynômes, à la fois d'une et de plusieurs variables et leurs degrés absolus:
| Polynôme | degré |
|---|---|
| 3x4+5x3-2x + 3 | 4 |
| 7x3-2xdeux+3x-6 | 3 |
| 6 | 0 |
| x-1 | 1 |
| X5-bx4+abx3+un B3Xdeux | 6 |
| 3x3Oui5 + 5xdeuxOui4 - 7xydeux + 6 | 8 |
Les deux derniers polynômes ont plus d'une variable. Parmi ceux-ci, le terme avec le degré absolu le plus élevé a été mis en évidence en gras, afin que le lecteur puisse vérifier rapidement le degré. Il est important de se rappeler que lorsque la variable n'a pas d'exposant écrit, on comprend que ledit exposant est égal à 1.
Par exemple dans le terme présenté un B3Xdeux il y a trois variables, à savoir: à, b Oui X. Dans ce terme, à est élevé à 1, c'est-à-dire:
a = a1
Donc un B3Xdeux = a1b3Xdeux
Puisque l'exposant de b est 3 et celui de x est 2, il s'ensuit immédiatement que le degré de ce terme est:
1 + 3 + 2 = 6
Y est le degré absolu du polynôme, car aucun autre terme n'a un degré plus élevé.
Lorsque vous travaillez avec des polynômes, il est important de faire attention au degré de celui-ci, car d'abord et avant d'effectuer toute opération, il est pratique de suivre ces étapes, dans lesquelles le degré fournit des informations très importantes:
-Ordonner le polynôme de préférence dans une direction décroissante. De cette façon, le terme avec le degré le plus élevé est à gauche et le terme avec le degré le plus bas est à droite..
-Réduire les termes similaires, une procédure qui consiste à ajouter algébriquement tous les termes de même variable et degré trouvés dans l'expression.
-Si nécessaire, les polynômes sont complétés, en insérant des termes dont le coefficient est 0, au cas où il manquerait des termes avec un exposant.
Étant donné le polynôme P (x) = 6xdeux - 5x4- 2x + 3x + 7 + 2x5 - 3x3 + X7 -12 il est demandé de le classer par ordre décroissant, de réduire les termes similaires s'il y en a et de compléter les termes manquants si nécessaire.
La première chose à rechercher est le terme avec le plus grand exposant, qui est le degré du polynôme, qui s'avère être:
X7
Donc P (x) est de degré 7. Ensuite, le polynôme est ordonné, en commençant par ce terme à gauche:
P (x) = x7 + 2x5 - 5x4 - 3x3 + 6xdeux - 2x + 3x + 7 à 12
Maintenant, les termes similaires sont réduits, qui sont les suivants: - 2x et 3x d'une part. Et 7 et -12 de l'autre. Pour les réduire, les coefficients sont ajoutés algébriquement et la variable reste inchangée (si la variable n'apparaît pas à côté du coefficient, rappelez-vous que x0 = 1):
-2x + 3x = x
7 -12 = -5
Remplacez ces résultats par P (x):
P (x) = x7 +2x5 - 5x4 - 3x3 + 6xdeux + x -5
Et enfin le polynôme est examiné pour voir s'il manque un exposant et en effet, un terme dont l'exposant est 6 est manquant, donc il est complété par des zéros comme ceci:
P (x) = x7 + 0x6 +2x5 - 5x4 - 3x3 + 6xdeux + x - 5
On observe maintenant que le polynôme a été laissé avec 8 termes, car comme dit précédemment, le nombre de termes est égal au degré + 1.
Avec les polynômes, vous pouvez effectuer des opérations d'addition et de soustraction, dans lesquelles seuls des termes similaires sont ajoutés ou soustraits, qui sont ceux avec la même variable et le même degré. S'il n'y a pas de termes similaires, l'addition ou la soustraction est simplement indiquée.
Une fois l'addition ou la soustraction effectuée, cette dernière étant la somme du contraire, le degré du polynôme résultant est toujours égal ou inférieur au degré du polynôme additionnant le degré le plus élevé.
Trouvez la somme suivante et déterminez son degré absolu:
à3- 8axdeux + X3 + 5edeuxx - 6axdeux - X3 + 3e3 - 5edeuxx - x3 + à3+ 14axdeux - X3
C'est un polynôme à deux variables, il est donc pratique de réduire les termes similaires:
à3- 8axdeux + X3 + 5edeuxx - 6axdeux - X3 + 3e3 - 5edeuxx - x3 + à3+ 14axdeux - X3 =
= a3 + 3e3 + à3 - 8axdeux - 6axdeux+ 14axdeux +5edeuxx - 5edeuxx + x3- X3- X3- X3 =
= 5a3 - 2x3
Les deux termes sont de degré 3 dans chaque variable. Par conséquent, le degré absolu du polynôme est 3.
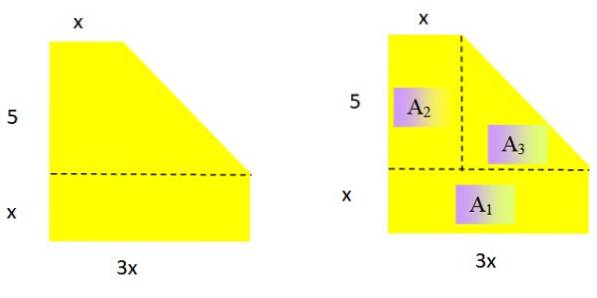
Exprimez l'aire de la figure géométrique plane suivante sous forme de polynôme (figure 2 à gauche). Quel est le degré du polynôme résultant?
Étant une aire, le polynôme résultant doit être de degré 2 dans la variable x. Pour déterminer une expression appropriée pour la zone, la figure est décomposée en zones connues:
L'aire d'un rectangle et d'un triangle sont respectivement: base x hauteur Oui base x hauteur / 2
À1 = x. 3x = 3xdeux; Àdeux = 5. x = 5x; À3 = 5. (2x / 2) = 5x
Noter: la base du triangle est 3x - x = 2x et sa hauteur est 5.
Maintenant, les trois expressions obtenues sont ajoutées, avec cela nous avons l'aire de la figure en fonction de X:
3xdeux + 5x + 5x = 3xdeux + 10x
Personne n'a encore commenté ce post.