
Définition de l'hypercube, dimensions, coordonnées, déplié
UNE hypercube est un cube de dimension n. Le cas particulier de l'hypercube à quatre dimensions est appelé tesseract. Un hypercube ou n-cube se compose de segments droits, tous de même longueur orthogonaux à leurs sommets.
Les êtres humains perçoivent un espace tridimensionnel: largeur, hauteur et profondeur, mais il ne nous est pas possible de visualiser un hypercube de dimension supérieure à 3.
Tout au plus nous pouvons en faire des projections dans un espace tridimensionnel pour le représenter, de la même manière que nous projetons un cube sur un plan pour le représenter..
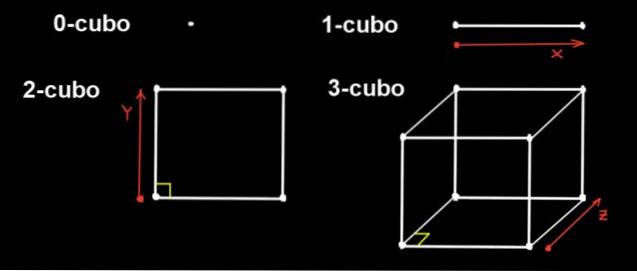
Dans la dimension 0, le seul chiffre est le point, donc un cube 0 est un point. Un 1-cube est un segment droit, qui est formé en déplaçant un point dans une direction sur une distance.
Pour sa part, un 2-cube est un carré. Il est construit en déplaçant le 1-cube (le segment de longueur a) dans la direction y, qui est orthogonale à la direction x, d'une distance a.
Le 3-cube est le cube commun. Il est construit à partir du carré en le déplaçant dans la troisième direction (z), qui est orthogonale aux directions x et y, une distance à.
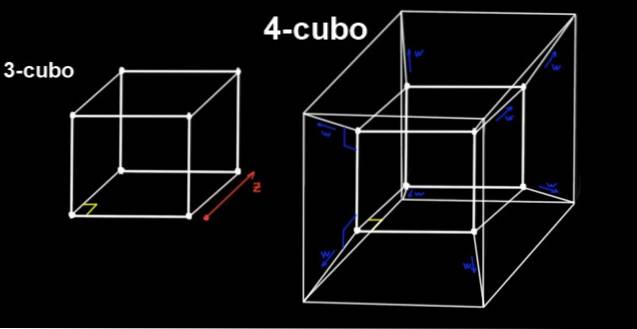
Le 4-cube est le tesseract, qui est construit à partir d'un 3-cube le déplaçant orthogonalement, une distance à, vers une quatrième dimension (ou quatrième direction), que nous ne pouvons pas percevoir.
Un tesseract a tous ses angles droits, il a 16 sommets et toutes ses arêtes (18 au total) ont la même longueur à.
Si la longueur des arêtes d'un n-cube ou d'un hypercube de dimension n est 1, alors c'est un hypercube unitaire, dans lequel la diagonale la plus longue mesure √n.

Index des articles
- 1 Que sont les dimensions?
- 1.1 L'espace tridimensionnel
- 2 Les coordonnées d'un hypercube
- 2.1 Déplier un hypercube
- 3 Références
Quelles sont les dimensions?
Les cotes sont les degrés de liberté ou les directions possibles dans lesquelles un objet peut se déplacer.
En dimension 0, il n'y a pas de possibilité de translation et le seul objet géométrique possible est le point.
Une dimension dans l'espace euclidien est représentée par une ligne ou un axe orienté qui définit cette dimension, appelé axe X. La séparation entre deux points A et B est la distance euclidienne:
d = √ [(xà - Xb)deux].
En deux dimensions, l'espace est représenté par deux lignes orientées orthogonales l'une par rapport à l'autre, appelées axe X et axe Y..
La position de tout point dans cet espace bidimensionnel est donnée par sa paire de coordonnées cartésiennes (x, y) et la distance entre deux points A et B sera:
d = √ [(xà - Xb)deux + (Oà - Ouib)deux]
Parce que c'est un espace où la géométrie d'Euclide est remplie.
Espace tridimensionnel
L'espace tridimensionnel est l'espace dans lequel nous nous déplaçons. Il a trois directions: largeur, hauteur et profondeur.
Dans une pièce vide les coins perpendiculaires les uns aux autres donnent ces trois directions et à chacune on peut associer un axe: X, Y, Z.
Cet espace est également euclidien et la distance entre deux points A et B est calculée comme suit:
d = √ [(xà - Xb)deux + (Oà - Ouib)deux + (zà - zb)deux]
Les êtres humains ne peuvent pas percevoir plus de trois dimensions spatiales (ou euclidiennes).
Cependant, d'un point de vue strictement mathématique, il est possible de définir un espace euclidien à n dimensions.
Dans cet espace, un point a des coordonnées: (x1, x2, x3,…, xn) et la distance entre deux points est:
d = √ [(x1er - X1 B)deux + (X2e - X2b)deux +… + (Xn / A - Xnb)deux].
La quatrième dimension et le temps
En effet, dans la théorie de la relativité, le temps est traité comme une dimension de plus et une coordonnée lui est associée.
Mais il faut préciser que cette coordonnée associée au temps est un nombre imaginaire. Par conséquent, la séparation de deux points ou événements dans l'espace-temps n'est pas euclidienne, mais suit plutôt la métrique de Lorentz.
Un hypercube à quatre dimensions (le tesseract) ne vit pas dans l'espace-temps, il appartient à un hyper-espace euclidien à quatre dimensions.

Les coordonnées d'un hypercube
Les coordonnées des sommets d'un n-cube centré à l'origine sont obtenues en faisant toutes les permutations possibles de l'expression suivante:
(a / 2) (± 1, ± 1, ± 1,…., ± 1)
Où a est la longueur du bord.
-le le volume d'un n-cube d'arête a est: (a / 2)n (deuxn) = unn.
-La la plus longue diagonale est la distance entre les sommets opposés.
-Les suivants sont sommets opposés dans un carré: (-1, -1) et (+1, +1).
-Et dans un cube: (-1, -1, -1) et (+1, +1, +1).
-La la plus longue diagonale d'un n-cube mesure:
d = √ [1 - (- 1))deux +… + (1 - (- 1))deux] = √ [n 2deux] = 2√n
Dans ce cas, le côté a été supposé être a = 2. Pour un n-cube de n'importe quel côté, ce qui suit restera:
d = a√n.
-Un tesseract a chacun de ses 16 sommets connectés à quatre arêtes. La figure suivante montre comment les sommets sont connectés dans un tesseract.
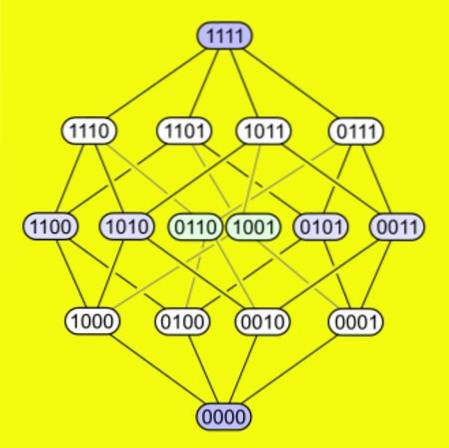
Dépliage d'un hypercube
Une figure géométrique régulière, par exemple un polyèdre, peut être dépliée en plusieurs figures de moindre dimensionnalité.
Dans le cas d'un 2-cube (un carré), il peut être déplié en quatre segments, c'est-à-dire quatre 1-cube.
De même, un 3-cube peut être déplié en six 2-cube.

Un 4-cube (tesseract) peut être déplié en huit 3-cube.
L'animation suivante montre le déroulement d'un tesseract.

Les références
- Culture scientifique. Hypercube, visualisant la quatrième dimension. Récupéré de: culturacientifica.com
- Epsilons. Hypercube ou tesseract en quatre dimensions. Récupéré de: epsilones.com
- Perez R, Aguilera A. Une méthode pour obtenir un tesseract à partir du développement d'un hypercube (4D). Récupéré de: researchgate.net
- Wikibooks. Mathématiques, polyèdres, hypercubes. Récupéré de: es.wikibooks.org
- Wikipédia. Hypercube. Récupéré de: en.wikipedia.com
- Wikipédia. Tesseract. Récupéré de: en.wikipedia.com


Personne n'a encore commenté ce post.