
Propriétés, types et exemples d'homothétie
La homothétie C'est un changement géométrique dans le plan où, à partir d'un point fixe appelé le centre (O), les distances sont multipliées par un facteur commun. De cette façon, chaque point P correspond à un autre point P 'produit de la transformation, et ceux-ci sont alignés avec le point O.
Ensuite, l'homothétie concerne une correspondance entre deux figures géométriques, où les points transformés sont appelés homothétiques, et ceux-ci sont alignés avec un point fixe et avec des segments parallèles entre eux..

Index des articles
- 1 Homothécie
- 2 propriétés
- 3 types
- 3.1 Homothétie directe
- 3.2 Homothétie inverse
- 4 Composition
- 5 exemples
- 5.1 Premier exemple
- 5.2 Deuxième exemple
- 6 Références
Homothécie
L'homothétie est une transformation qui n'a pas d'image congruente, car à partir d'une figure, une ou plusieurs figures de plus ou moins grande taille que la figure originale seront obtenues; c'est-à-dire que l'homothétie transforme un polygone en un autre similaire.
Pour que l'homothétie soit remplie, point à point et ligne à ligne doivent correspondre, de sorte que les paires de points homologues soient alignées avec un troisième point fixe, qui est le centre de l'homothétie..
De même, les paires de lignes qui les joignent doivent être parallèles. La relation entre ces segments est une constante appelée rapport d'homothétie (k); de telle manière que l'homothétie peut être définie comme:
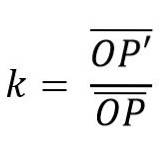
Pour réaliser ce type de transformation, on commence par choisir un point arbitraire, qui sera le centre de l'homothétie.
À partir de ce point, des segments de ligne sont dessinés pour chaque sommet de la figure à transformer. L'échelle dans laquelle se fait la reproduction de la nouvelle figure est donnée par le rapport d'homothétie (k).
Propriétés
L'une des principales propriétés de l'homothétie est que, par la raison homothétique (k), toutes les figures homothétiques sont similaires. Les autres propriétés notables sont les suivantes:
- Le centre de l'homothécie (O) est le seul point double et il devient lui-même; c'est-à-dire que cela ne varie pas.
- Les lignes qui passent par le centre se transforment en elles-mêmes (elles sont doubles), mais les points qui le composent ne sont pas doubles.
- Les lignes qui ne passent pas par le centre deviennent des lignes parallèles; de cette façon, les angles d'homothétie restent les mêmes.
- L'image d'un segment par une homothétie de centre O et de rapport k, est un segment parallèle à celui-ci et a k fois sa longueur. Par exemple, comme on peut le voir sur l'image suivante, un segment AB par homothétie se traduira par un autre segment A'B ', de telle sorte que AB sera parallèle à A'B' et le k sera:
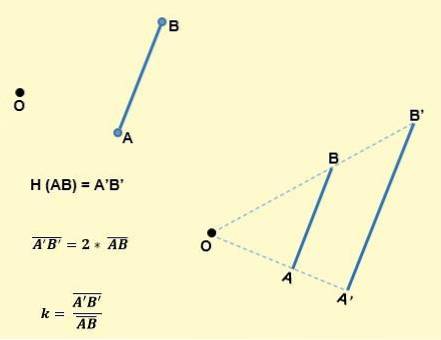
- Les angles homothétiques sont congruents; c'est-à-dire qu'ils ont la même mesure. Par conséquent, l'image d'un angle est un angle qui a la même amplitude.
En revanche, l'homothétie varie en fonction de la valeur de son rapport (k), et les cas suivants peuvent se produire:
- Si la constante k = 1, tous les points sont fixes car ils se transforment. Ainsi, la figure homothétique coïncide avec celle d'origine et la transformation sera appelée fonction d'identité.
- Si k ≠ 1, le seul point fixe sera le centre de l'homothétique (O).
- Si k = -1, l'homothétie devient une symétrie centrale (C); c'est-à-dire qu'une rotation se produira autour de C, à un angle de 180ou alors.
- Si k> 1, la taille de la figure transformée sera plus grande que la taille de l'original.
- Oui 0 < k < 1, el tamaño de la figura transformada será menor que el de la original.
- Oui -1 < k < 0, el tamaño de la figura transformada será menor y estará girada con respecto a la original.
- Si k < -1, el tamaño de la figura transformada será mayor y estará girada con respecto a la original.
Les types
L'homothétie peut également être classée en deux types, en fonction de la valeur de son rapport (k):
Homothétie directe
Cela se produit si la constante k> 0; c'est-à-dire que les points homothétiques sont du même côté par rapport au centre:
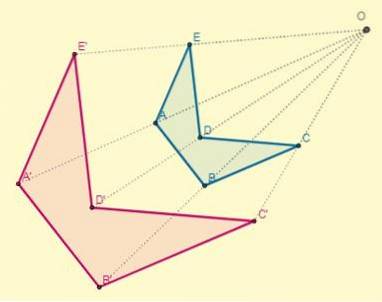
Le facteur de proportionnalité ou le rapport de similitude entre les chiffres homothétiques directs sera toujours positif.
Homothétie inversée
Cela se produit si la constante k < 0; es decir, los puntos iniciales y sus homotéticos se ubican en los extremos opuestos con respecto al centro de la homotecia pero alineados a esta. El centro se encontrará entre las dos figuras:
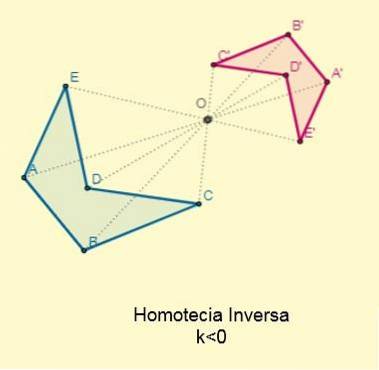
Le facteur de proportionnalité ou le rapport de similitude entre les chiffres homothétiques inverses sera toujours négatif.
Composition
Lorsque plusieurs mouvements sont successivement effectués jusqu'à l'obtention d'un chiffre égal à l'original, une composition de mouvements se produit. La composition de plusieurs mouvements est aussi un mouvement.
La composition entre deux homothécies aboutit à une nouvelle homothétie; c'est-à-dire qu'il existe un produit d'homothéties dans lequel le centre sera aligné avec le centre des deux transformations d'origine, et le rapport (k) est le produit des deux rapports.
Ainsi, dans la composition de deux homothécies H1(OU ALORS1, k1) et Hdeux(OU ALORSdeux, kdeux), la multiplication de leurs ratios: k1 x kdeux = 1 se traduira par une homothétie du rapport k3 = K1 x kdeux. Le centre de cette nouvelle homothétie (O3) sera situé sur la ligne O1 OU ALORSdeux.
L'homothécie correspond à un changement plat et irréversible; si deux homothéties sont appliquées qui ont le même centre et le même rapport mais avec un signe différent, la figure originale sera obtenue.
Exemples
Premier exemple
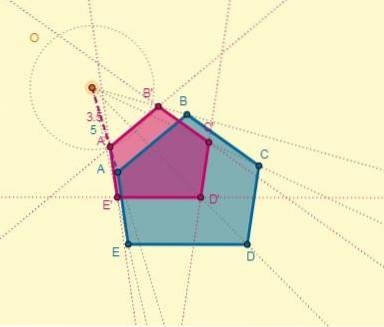
Appliquer une homothétie au polygone donné de centre (O), situé à 5 cm du point A et dont le rapport est k = 0,7.
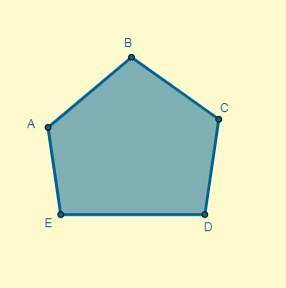
Solution
N'importe quel point est choisi comme centre de l'homothétie, et à partir de ce point, les rayons sont dessinés à travers les sommets de la figure:
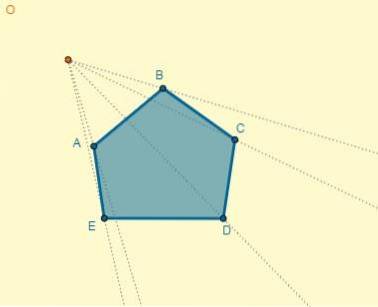
Nous avons que la distance du centre (O) au point A est OA = 5; Avec cela, la distance de l'un des points homothétiques (OA ') peut être déterminée, sachant également que k = 0,7:
OA '= k x OA.
OA '= 0,7 x 5 = 3,5.
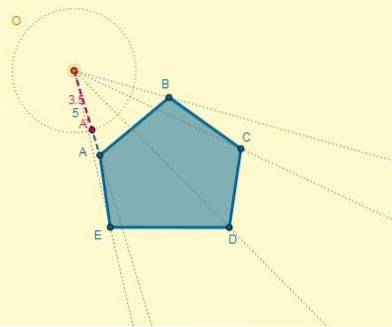
Le processus peut être effectué pour chaque sommet, ou le polygone homothétique peut également être dessiné en se souvenant que les deux polygones ont des côtés parallèles:
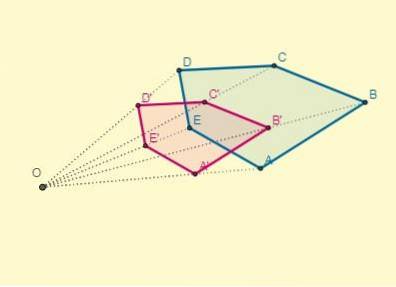
Enfin, la transformation ressemble à ceci:
Deuxième exemple
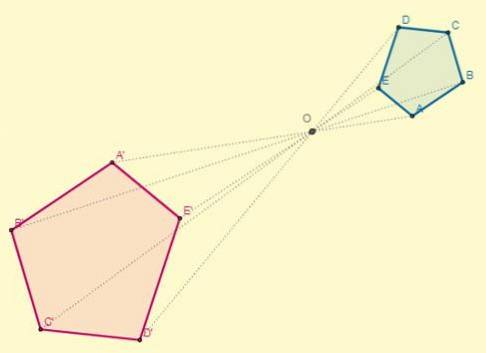
Appliquer une homothétie au polygone donné de centre (O), situé à 8,5 cm du point C et dont le rapport y k = -2.
Solution
La distance du centre (O) au point C est OC = 8,5; Avec ces données, il est possible de déterminer la distance d'un des points homothétiques (OC '), sachant également que k = -2:
OC '= k x OC.
OC '= -2 x 8,5 = -17
Après avoir tracé les segments des sommets du polygone transformé, les points initiaux et leurs homothèses sont situés aux extrémités opposées par rapport au centre:
Les références
- Álvaro Rendón, A. R. (2004). Dessin technique: cahier d'activités.
- Antonio Álvarez de la Rosa, J. L. (2002). Affinité, homologie et homothécie.
- Baer, R. (2012). Algèbre linéaire et géométrie projective. Société de messagerie.
- Hebert, Y. (1980). Mathématiques générales, probabilités et statistiques.
- Meserve, B. E. (2014). Concepts fondamentaux de la géométrie. Société de messagerie.
- Nachbin, L. (1980). Introduction à l'algèbre. Reverte.



Personne n'a encore commenté ce post.