La inductance mutuelle décrit l'interaction entre deux bobines voisines 1 et 2, par laquelle un courant variable je circulant à travers la bobine 1, produit un flux de champ magnétique variable à travers la bobine 2.
Ledit flux est proportionnel au courant et la constante de proportionnalité est l'inductance mutuelle M12. Soit ΦB2 le flux de champ magnétique à travers la bobine 2, vous pouvez alors écrire:
ΦB2 = M12 je1
Et si la bobine 2 a Ndeux se tourne:
Ndeux . ΦB2 = M12 je1
De cette manière, l'inductance mutuelle ou coefficient d'inductance mutuelle M12 entre les deux bobines est:
M12 = Ndeux . ΦB2 / JE1
L'inductance mutuelle a des unités de Weber / Ampère ou Wb / A, qui est appelée Henry ou Henry et est abrégée H. Par conséquent, 1 Henry équivaut à 1 Wb / A.
La valeur de M12 Cela dépend de la géométrie entre les bobines, de leur forme, de leur taille, du nombre de tours de chacune et de la distance qui les sépare, ainsi que de la position relative entre elles.
Index des articles
Le phénomène d'inductance mutuelle a de nombreuses applications grâce au fait que son origine est dans la loi de Faraday-Lenz, qui stipule que les courants variables dans un circuit induisent des courants et des tensions dans un autre, sans qu'il soit nécessaire que les circuits soient connectés par des câbles..
Lorsque deux circuits interagissent de cette manière, on dit qu'ils sont couplés magnétiquement. De cette manière, l'énergie peut passer de l'une à l'autre, une circonstance qui peut être utilisée de différentes manières, comme l'a démontré Nikola Tesla au début du 20e siècle (voir exercice résolu 1).
Dans sa quête pour transmettre de l'électricité sans fil, Tesla a expérimenté divers appareils. Grâce à ses découvertes, le transformateur a été créé, l'appareil qui transfère l'énergie électrique des centrales électriques aux maisons et aux industries.
Transformateur
Le transformateur transmet des tensions alternatives très élevées dans les lignes électriques, minimisant ainsi les pertes de chaleur et en même temps fournissant une énergie maximale aux consommateurs.
Lorsque la tension atteint ces derniers, elle doit être abaissée, ce qui est obtenu avec le transformateur. Il se compose de deux bobines de fil enroulées autour d'un noyau de fer. L'une des bobines avec N1 tours est connecté à une tension alternative et est appelé primaire. L'autre, qui est le secondaire, a Ndeux tourne, se connecte à une résistance.
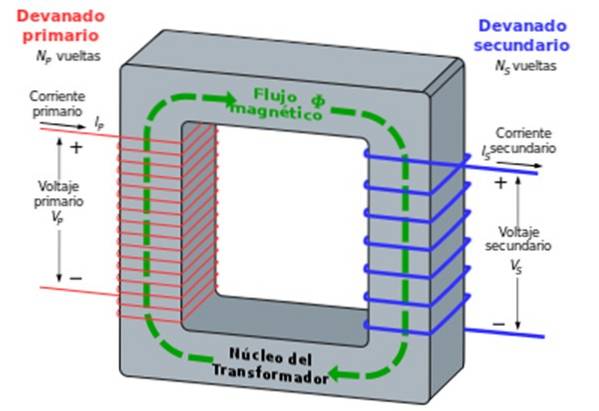
Le noyau de fer garantit que toutes les lignes de champ magnétique qui traversent une bobine passent également par l'autre..
La loi de Faraday stipule que le rapport entre les tensions Vdeux / V1 (secondaire / primaire) est égal au rapport entre le nombre de tours Ndeux / N1:
Vdeux / V1 = Ndeux / N1
En ajustant correctement le nombre de tours, une tension supérieure ou inférieure à celle de l'entrée est obtenue en sortie.
Les transformateurs sont construits dans de nombreuses tailles, des énormes transformateurs dans les installations électriques aux chargeurs pour téléphones portables, ordinateurs portables, lecteurs MP3 et autres appareils électroniques..
Les effets de l'inductance mutuelle sont également présents dans les stimulateurs cardiaques pour maintenir la fréquence du rythme cardiaque, de sorte que le cœur puisse maintenir la circulation sanguine stable..
Les stimulateurs cardiaques sont alimentés par batterie. Lorsque ceux-ci sont épuisés, une bobine externe est capable de transmettre de l'énergie à une autre bobine qui se trouve à l'intérieur du stimulateur cardiaque. La procédure étant réalisée par induction, il n'est pas nécessaire de soumettre le patient à une nouvelle intervention lorsque la batterie est épuisée.
Les chargeurs sans fil pour différents objets tels que les brosses à dents et les téléphones portables, qui sont des appareils à faible consommation d'électricité, constituent une autre application courante..
À l'avenir, l'utilisation de chargeurs sans fil pour les batteries de voitures électriques est envisagée. Et de nombreuses recherches visent aujourd'hui à produire de l'électricité sans fil dans les foyers. L'une des principales limitations à l'heure actuelle est la distance à laquelle les courants peuvent être induits grâce aux champs magnétiques.
Dans une version de la bobine Tesla, utilisée comme générateur haute tension dans certaines démonstrations en laboratoire, vous disposez d'un long solénoïde de longueur L, rayon R1 avec N1 tours par unité de longueur, entourés coaxialement d'une bobine circulaire de rayon Rdeux et ndeux se tourne.
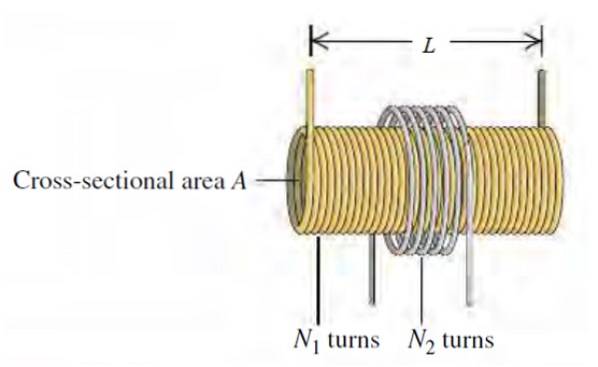
a) Trouvez l'inductance mutuelle M du circuit, dépend-elle du courant traversant le solénoïde?
b) L'inductance mutuelle dépend-elle de la forme de la bobine ou du fait que ses spires sont plus ou moins enroulées ensemble??
L'amplitude du champ magnétique du solénoïde est proportionnelle au nombre de tours et au courant qui le traverse, ce qui est noté i1, puisque le solénoïde est le circuit 1. Il est donné par l'expression:
B1 = μou alorsN1.je1 / L
Le flux de champ magnétique que le solénoïde crée dans un tour de la bobine, qui est le circuit 2, est le produit de l'intensité du champ et de la zone délimitée par le champ:
ΦB2 = B1. À1
Où aller1 est la section transversale du solénoïde et non de la bobine, car le champ de solénoïde est nul en dehors de celui-ci:
À1 = π (R1)deux
Nous substituons l'aire dans l'équation pour ΦB2:
ΦB2 = B1. π (R1)deux = (μou alorsN1.je1 / L). π (R1)deux
Et l'inductance mutuelle est donnée par:
M12 = Ndeux . ΦB2 / JE1 = Ndeux. [(μou alorsN1.je1 / L). π (R1)deux ] / JE1
M12 = μou alors N1 Ndeux . π (R1)deux / L
Cela ne dépend pas du courant traversant le solénoïde, dont nous avons vu qu'il est annulé.
Comme nous pouvons le voir, l'inductance mutuelle ne dépend pas de la forme de la bobine, ni de la tension des spires. La seule influence de la bobine sur l'inductance mutuelle est le nombre de spires qu'elle contient, qui est Ndeux.
Deux bobines sont très proches l'une de l'autre et l'une d'elles transporte un courant variable dans le temps donné par l'équation suivante:
i (t) = 5,00 e -0,0250 t sin (377 t) A
À t = 0,800 seconde, la tension induite dans la deuxième bobine est mesurée, obtenant -3,20 V. Trouver l'inductance mutuelle des bobines.
Nous utilisons l'équation:
εdeux = - M12 (donné1/ dt)
Nous appelons l'inductance mutuelle entre les bobines simplement M, puisque généralement M12 = Mvingt-et-un. Nous aurons besoin de la première dérivée du courant par rapport au temps:
donné1/ dt =
= - 0,0250 x 5,00 e -0,0250 t x sin (377 t) - 377 cos (377 t) x 5,00 e -0,0250 t As
Nous évaluons cette dérivée à t = 0,800 s:
donné1/ dt = - 0,0250 x 5,00 e -0,0250 x 0,800 x sin (377 x 0,800) - 377 cos (377 x 0,800) x 5,00 e -0,0250 x 0,800 A / s =
= -5,00 e -0,0250 x 0,800 [0,0250 x sin (377 x 0,800) + 377 cos (377 x 0,800)] =
= -1847,63 A / s
M = -3,20 V / -1847,63 A / s = 0,001732 H = 1,73 mH.
Personne n'a encore commenté ce post.