
Formules, exemples, applications, exercices de la loi de Hooke
La la loi de Hooke souligne que la déformation subie par un objet élastique est directement proportionnelle à la force qui lui est appliquée. La constante de proportionnalité dépend de la nature de l'objet, de sa géométrie et du matériau avec lequel il est fabriqué..
Tous les matériaux ont des propriétés élastiques dans une plus ou moins grande mesure, ils sont donc conformes à la loi de Hooke tant qu'ils reviennent à leurs dimensions d'origine, une fois que la force cesse. Les ressorts et les élastiques sont de bons exemples d'objets qui répondent à la loi de Hooke, tout comme les goupilles en acier qui font partie d'un pont..

En prenant un ressort ou un ressort comme exemple, pour le maintenir tendu ou comprimé, il est nécessaire d'appliquer une force dont la magnitude est F.Selon la loi de Hooke, le ressort subira une déformation x:
F ∝ x
La constante de proportionnalité, qui étant un ressort s'appelle constante de rigidité du ressort, est noté k, donc:
F = k⋅x
Dans les unités du Système International, la force est en newton (N) et la déformation en mètres (m). Par conséquent, la constante de ressort a des unités de N / m. La constante du ressort représente la force qui doit être appliquée pour la déformer de 1 m de longueur.
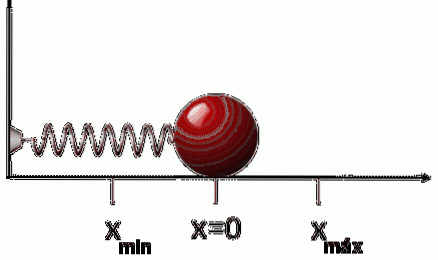
Si, après avoir étiré ou comprimé le ressort, il est relâché, il se déplacera dans le sens opposé à la force appliquée. Cela signifie que si nous l'étirons, il se comprime et vice versa. D'où la force FR Quoi le ressort exerce c'est:
FR = -k⋅x
Le signe négatif indique ce qui précède: que la force s'oppose au déplacement, donc cette force est connue sous le nom de force réparatrice.
Index des articles
- 1 Formule et équations
- 1.1 Travaux effectués pour étirer ou comprimer un ressort
- 2 Exemples de ressorts
- 2.1 Ressort de compression
- 2.2 Ressorts d'extension et de torsion
- 2.3 Matériaux pour la fabrication des ressorts
- 3 Applications de la loi de Hooke
- 4 exercices résolus
- 4.1 - Exercice 1
- 4.2 - Exercice 2
- 5 Références
Formule et équations
La relation entre la force et le déplacement dans un ressort a été découverte par Robert Hooke (1635-1703), un physicien anglais notable connu pour sa rivalité avec Isaac Newton. Hooke était un scientifique polyvalent qui s'est aventuré avec succès dans différents domaines scientifiques: mécanique, biologie, astronomie et architecture..

Hooke s'est rendu compte que si la force appliquée à un ressort n'est pas très grande, le ressort se déforme proportionnellement à la force, et une fois que cette force disparaît, le ressort revient à sa longueur naturelle..
Ainsi, la loi de Hooke sous forme graphique se présente sous la forme d'une ligne droite dont la pente est la constante de ressort. L'image suivante montre la force exercée sur le ressort pour l'étirer - ou le comprimer - en fonction de la position x. Notez également que la force ne dépend pas de la longueur naturelle du ressort, mais de son déplacement..
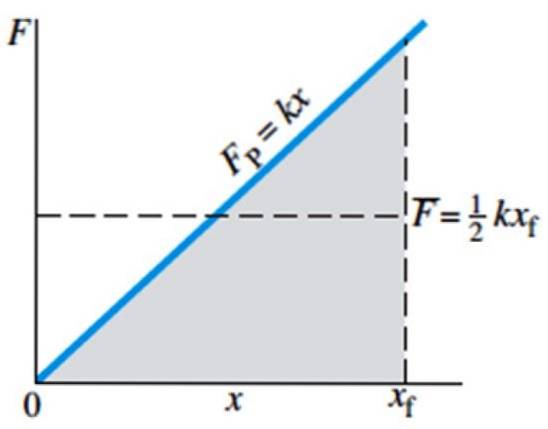
La force moyenne est indiquée sur le graphique par la barre F et est égale à ½ kxF, où xF est la position finale du ressort.
La force exercée sur le ressort et la force qu'il exerce sur un objet qui lui est lié sont des forces variables. Plus vous souhaitez étirer ou comprimer le ressort, plus vous devez appliquer de force pour y parvenir..
Travail effectué pour étirer ou comprimer un ressort
Lorsqu'une force de déformation est appliquée au ressort, un travail est effectué qui est stocké dans le ressort et peut être utilisé plus tard..
Le travail mécanique est défini comme l'aire sous le graphique de la force F en fonction de la position x. Pour calculer le travail W effectué par une force variable F (x) lors du déplacement d'un objet de la position x1 jusqu'à la position xdeux il faut calculer l'intégrale définie:
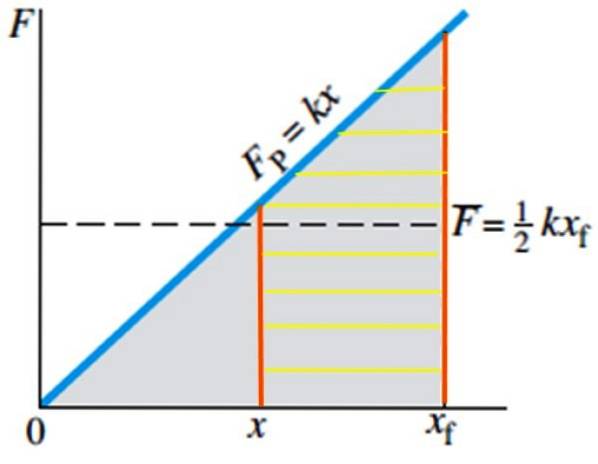
Dans le cas des travaux nécessaires pour amener un ressort de sa position d'équilibre à la position xF C'est très simple, puisque l'aire à calculer est celle du triangle grisé sur la figure 4, dont la formule est connue:
Aire du triangle = ½ base. la taille
Par conséquent, le travail nécessaire est:
W = ½ xF . (kxF) = ½ k (xF)deux
Et si vous voulez calculer le travail nécessaire pour amener le ressort de la position x à la position xF, équivaudrait à calculer l'aire du trapèze hachuré de la figure 5:
W = ½ k (xF)deux - ½ k xdeux

Exemples de ressorts
Selon l'application à laquelle ils sont destinés, les ressorts peuvent être hélicoïdaux, cylindriques, coniques, spiralés, de section circulaire (la plus courante), carrée ou rectangulaire..
Une classification largement utilisée est selon le type d'effort auquel ils vont être soumis: il existe des ressorts de torsion, de flexion, de compression et d'extension. Ces derniers sont largement utilisés et certains fonctionnent également pour la tension et la compression..
Ressort de compression
Un exemple de ressort de compression est celui utilisé dans le jouet appelé pogo ou alors bâton de saut. Ces ressorts stockent beaucoup d'énergie potentielle lorsqu'ils sont comprimés et la libèrent petit à petit en revenant à la position d'équilibre. De cette façon, les rebonds ne sont pas trop brusques.

Ressorts d'extension et de torsion
Les ressorts de trampoline sont du type à ressort d'extension et sont fabriqués avec des bobines étroitement enroulées, avec deux crochets aux extrémités. Ils sont capables de retenir beaucoup d'énergie potentielle, qu'ils libèrent ensuite lorsque quelqu'un grimpe et commence à sauter sur le tapis, qui a également sa propre réponse élastique, comme tous les matériaux..
Les ressorts de torsion sont très courants, car ils sont utilisés pour fabriquer des pinces à linge. Au lieu de crochets aux extrémités, ils se plient à un angle pour résister aux forces de torsion.

Matériaux pour la fabrication de ressorts
Les matériaux les plus appropriés pour la fabrication des ressorts sont ceux avec un résistance ultime (résistance finale) élevée, c'est-à-dire qu'ils supportent un grand effort avant de se casser. Il est également souhaitable que le matériau ait une limite d'élasticité élevée, de sorte qu'il ne perde pas ses qualités élastiques avec de petits efforts..
Les ressorts robustes sont fabriqués à partir d'alliages, y compris l'acier à haute teneur en carbone, le cuivre, le nickel et le bronze.
Applications de la loi de Hooke
Étant donné que les ressorts ont le mérite de stocker de l'énergie potentielle lorsqu'ils sont étirés ou comprimés, ils sont capables de travailler en déplaçant des choses comme des mécanismes..
De cette manière, les ressorts ont une multitude d'applications, des petits objets du quotidien, en passant par les automobiles, aux machines de toutes sortes. Les ressorts servent à:
-Amortir les vibrations.
-Fabrication de mécanismes rétractables: stylos, pinces à linge, pinces à cheveux.
-Fabriquer des balances à ressort ou des dynamomètres
Et ils font également partie du mécanisme de:
-Horloges.
-Trampolines.
-Serrures.
-Jouets.
-Armes.
-Mesureurs à aiguilles, par exemple le galvanomètre, utilisés pour mesurer les courants, les tensions et les résistances.
Exercices résolus
- Exercice 1
Une force de magnitude 5,0 N est appliquée à un ressort, provoquant l'étirement d'une longueur de 3,5 cm par rapport à sa longueur naturelle..
a) Combien s'étire-t-il lorsque la force appliquée est de 7 N?
b) Trouvez le travail effectué par la force appliquée pour étirer le ressort à 3,5 cm de sa longueur naturelle.
Solution pour
Sachant que le ressort est étiré de 3,5 cm en appliquant 5,0 N on peut calculer sa constante:
k = F / x = 5,0 N / 3,5 cm = 1,43 N / cm.
Lorsqu'une force de 7 N est appliquée, l'étirement suivant est obtenu:
x = F / k = 7,0 N / 1,43 N / m = 4,9 cm
Solution b
Le travail nécessaire pour déformer un ressort est donné par:
W = ½ kxdeux = 0,5 x 1,43 N / cm x (3,5 cm)deux = 8,76 N. cm = 8,76 N. 1 x 10 -deux m = 0,0876 J.
- Exercice 2
Un ressort de masse négligeable et de 10 cm de long est suspendu à un support. Si une masse de 2 kg y est suspendue, le ressort est étiré à 15 cm. Calculer:
a) La constante du ressort
b) La taille du ressort lorsqu'une masse de 3 kg est suspendue.
Solution pour
L'étirement du ressort est x = 15-10 cm = 5 cm
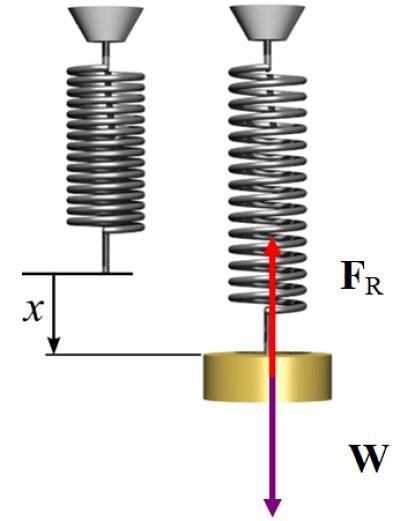
Le système étant en équilibre statique, la force exercée par le ressort lors de l'étirement est dirigée verticalement vers le haut, pour compenser le poids, qui est dirigé vers le bas, alors:
FR = W → kx = mg
k = 2 x 9,8 N / 5 x10 -deux m = 392 N / m
Solution b
Lorsqu'un poids de 3 kg est suspendu, la nouvelle force est W = 3 x 9,8 N = 29,4 N
Dans un tel cas, l'étirement est:
x = mg / k = 29. 4 N / 392 N / m = 0,075 m = 7,5 cm
Les références
- Bauer, W. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
- Blog sur les mécanismes créatifs. Quatre types de ressorts différents. Récupéré de: creativemechanisms.com.
- Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 2. Dynamique. Edité par Douglas Figueroa (USB).
- Giancoli, D. 2006. Physique: principes avec applications. 6e. Ed. Prentice Hall.
- .


Personne n'a encore commenté ce post.