La Loi de Lenz établit que la polarité de la force électromotrice induite en circuit fermé, due à la variation du flux de champ magnétique, est telle qu'elle s'oppose à la variation dudit flux.
Le signe négatif qui précède la loi de Faraday prend en considération la loi de Lenz, étant la raison pour laquelle elle est appelée loi de Faraday-Lenz et qui s'exprime comme suit:
Index des articles
ε représente la force électromotrice induite, abrégée en fem, Φ est le flux de champ magnétique et t C'est le moment. Unités du système international (SI) pour le fem sont les volts (V).
De son côté le flux de champ magnétique Φ est défini par le produit scalaire suivant:
Dans l'équation montrée B est constante et l'unité pour Φ dans le SI pour le flux de champ magnétique est le weber (W):
1 weber = 1 Tesla. métrodeux
Une autre façon d'exprimer Φ est celui obtenu en utilisant la définition de produit scalaire:
Φ = B.A.cos θ
Dans cette équation, B est la magnitude du champ magnétique (sans gras ni flèche, pour distinguer le vecteur de sa magnitude), A est la zone de la surface traversée par le champ et θ est l'angle entre les vecteurs B Oui n.
Le flux de champ magnétique peut varier de différentes manières au fil du temps pour créer un fem induit dans une boucle - un circuit fermé - de la zone A. Par exemple:
-Rendre le champ magnétique variable dans le temps: B = B (t), en gardant la surface et l'angle constants, puis:
%7D%7Bdt%7D=-B.A.sen%5Ctheta)
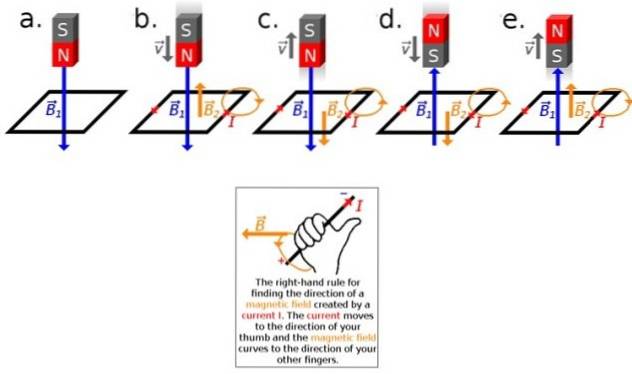
L'application immédiate de la loi de Lenz consiste à déterminer le sens de la fem ou courant induit sans aucun calcul. Considérez ce qui suit: vous avez une boucle au milieu d'un champ magnétique, comme celui produit par un barreau magnétique.
Si l'aimant et la boucle sont au repos l'un par rapport à l'autre, rien ne se passe, c'est-à-dire qu'il n'y aura pas de courant induit, car le flux de champ magnétique reste constant dans ce cas (voir figure 2a). Pour que le courant soit induit, le flux doit varier.
Maintenant, s'il y a un mouvement relatif entre l'aimant et la boucle, soit en déplaçant l'aimant vers la boucle, soit vers l'aimant, il y aura un courant induit à mesurer (Figure 2b et suivantes).
Ce courant induit génère à son tour un champ magnétique, donc nous aurons deux champs: celui de l'aimant B1 de couleur bleue et celle associée au courant créé par induction Bdeux, en orange.
La règle du pouce droit permet de connaître la direction de Bdeux, Pour ce faire, le pouce de la main droite est placé dans le sens et le sens du courant. Les quatre autres doigts indiquent la direction dans laquelle le champ magnétique se courbe, selon la figure 2 (ci-dessous).
Disons que l'aimant est lâché vers la boucle avec son pôle nord dirigé vers elle (figure 3). Les lignes de champ de l'aimant quittent le pôle nord N et entrent dans le pôle sud S. Ensuite, il y aura des changements dans in, le flux créé par B1 qui passe par la boucle:Φ augmente! Par conséquent, un champ magnétique est créé dans la boucle Bdeux avec une intention opposée.
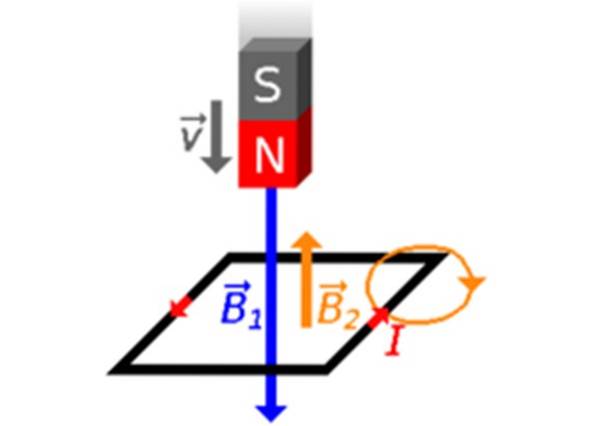
Le courant induit est dans le sens antihoraire, -flèches rouges dans les figures 2 et 3-, selon la règle du pouce droit.
Éloignons l'aimant de la boucle, puis son Φ diminue (figures 2c et 4), donc la boucle se précipite pour créer un champ magnétique à l'intérieur Bdeux dans la même veine, pour compenser. Par conséquent, le courant induit est horaire, comme on peut le voir sur la figure 4.
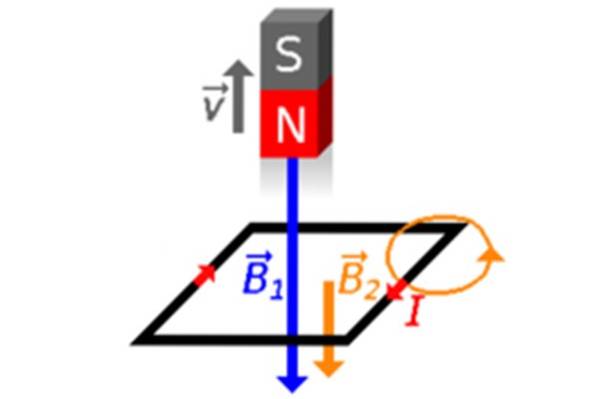
Que se passe-t-il si la position de l'aimant est inversée? Si le pôle sud pointe vers la boucle, le champ pointe vers le haut, puisque les lignes de B dans un aimant, ils quittent le pôle nord et entrent dans le pôle sud (voir figure 2d).
Immédiatement la loi de Lenz informe que ce champ vertical vers le haut, se précipitant vers la boucle, y induira un champ opposé, c'est-à-dire, Bdeux vers le bas et le courant induit sera également horaire.
Enfin, l'aimant est éloigné de la boucle, toujours avec son pôle sud pointant vers l'intérieur de celle-ci. Puis un champ est produit à l'intérieur de la boucle Bdeux pour éviter que l'éloignement de l'aimant ne modifie le flux de champ en lui. Tellement de B1 Quoi Bdeux aura la même signification (voir figure 2d).
Le lecteur se rendra compte que, comme promis, aucun calcul n'a été effectué pour connaître la direction du courant induit.
Heinrich Lenz (1804-1865) a réalisé de nombreux travaux expérimentaux tout au long de sa carrière scientifique. Les plus connus sont ceux que nous venons de décrire, dédiés à la mesure des forces magnétiques et des effets créés par la chute brutale d'un aimant au milieu d'une boucle. Avec ses résultats, il a affiné le travail de Michael Faraday.
Ce signe négatif dans la loi de Faraday s'avère être l'expérience la plus largement reconnue pour aujourd'hui. Cependant, Lenz a fait beaucoup de travail en géophysique pendant sa jeunesse, pendant ce temps, il était occupé à faire tomber des aimants dans des bobines et des tubes. Il a également fait des études sur la résistance électrique et la conductivité des métaux.
En particulier, sur les effets de l'augmentation de température sur la valeur de la résistance. Il n'a pas arrêté d'observer que lorsqu'un fil est chauffé, la résistance diminue et la chaleur se dissipe, ce que James Joule a également observé de manière indépendante..
Pour toujours se souvenir de ses contributions à l'électromagnétisme, en plus de la loi qui porte son nom, les inductances (bobines) sont désignées par la lettre L.
C'est une expérience dans laquelle il est démontré comment un aimant ralentit lorsqu'il est libéré dans un tube de cuivre. Lorsque l'aimant tombe, il génère des variations du flux de champ magnétique à l'intérieur du tube, comme cela se produit avec la boucle de courant..
Ensuite, un courant induit est créé qui s'oppose au changement de débit. Le tube crée pour cela son propre champ magnétique, qui, comme nous le savons déjà, est associé au courant induit. Supposons que l'aimant soit libéré avec le pôle sud vers le bas, (Figures 2d et 5).
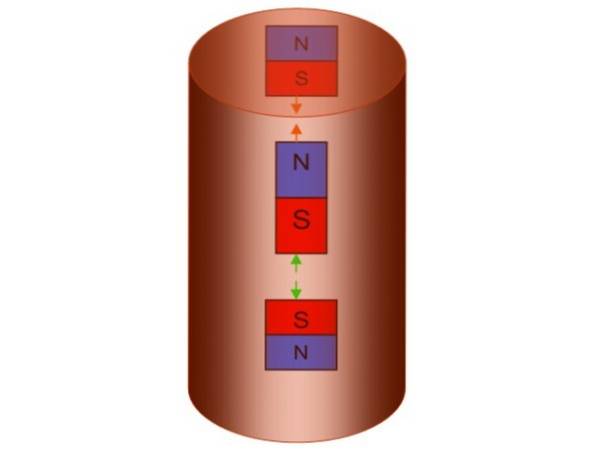
En conséquence, le tube crée son propre champ magnétique avec un pôle nord. vers le bas et un pôle sud en haut, ce qui équivaut à créer une paire d'aimants factices, un au-dessus et un en dessous de celui qui tombe.
Le concept est reflété dans la figure suivante, mais il faut se rappeler que les pôles magnétiques sont inséparables. Si l'aimant factice inférieur a un pôle nord vers le bas, il sera nécessairement accompagné d'un pôle sud vers le haut..
Au fur et à mesure que les opposés s'attirent et que les opposés se repoussent, l'aimant qui tombe sera repoussé et en même temps attiré par l'aimant fictif supérieur.
L'effet net sera toujours un freinage même si l'aimant est relâché avec le pôle nord vers le bas..
La loi de Joule-Lenz décrit comment une partie de l'énergie associée au courant électrique qui circule à travers un conducteur est perdue sous forme de chaleur, un effet qui est utilisé dans les radiateurs électriques, les fers à repasser, les sèche-cheveux et les brûleurs électriques, entre autres appareils..
Tous ont une résistance, un filament ou un élément chauffant qui chauffe au fur et à mesure que le courant passe..
Sous forme mathématique, laissez R la résistance de l'élément chauffant, je l'intensité du courant qui le traverse et t temps, la quantité de chaleur produite par l'effet Joule est:
Q = Ideux. R. t
Où Q Il est mesuré en joules (unités SI). James Joule et Heinrich Lenz ont découvert cet effet simultanément vers 1842.
Voici trois exemples importants où la loi Faraday-Lenz s'applique:
Un générateur de courant alternatif transforme l'énergie mécanique en énergie électrique. Le raisonnement a été décrit au début: une boucle tourne au milieu d'un champ magnétique uniforme, comme celui créé entre les deux pôles d'un gros électroaimant. Quand ils sont utilisés N vous tournez, le fem augmente proportionnellement à N.
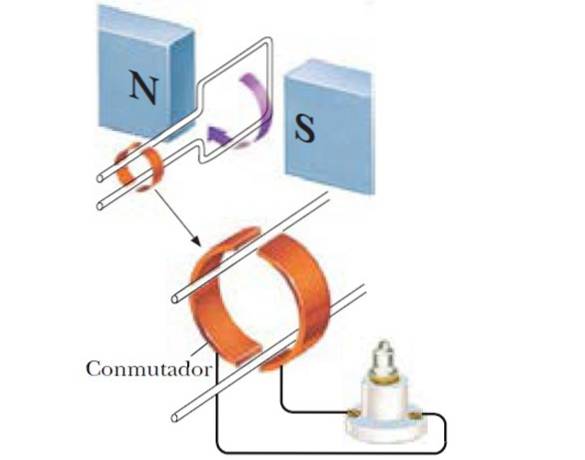
Au fur et à mesure que la boucle tourne, le vecteur normal à sa surface change son orientation par rapport au champ, produisant un fem qui varie de façon sinusoïdale avec le temps. Supposons que la fréquence angulaire de rotation soit ω, puis lors de la substitution dans l'équation qui a été donnée au début, nous aurons:
C'est un appareil qui permet d'obtenir une tension continue à partir d'une tension alternative. Le transformateur fait partie d'innombrables appareils, comme un chargeur de téléphone portable par exemple, il fonctionne comme suit:
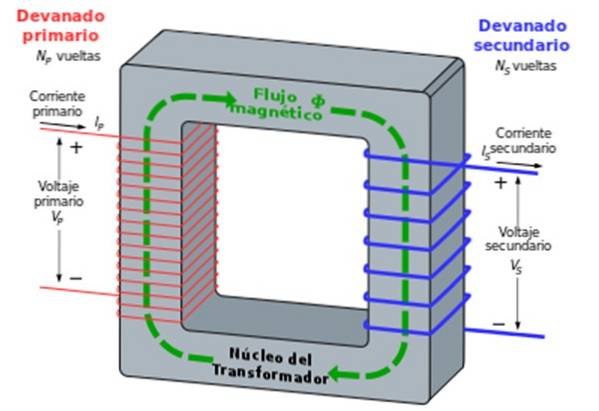
Il y a deux bobines enroulées autour d'un noyau de fer, l'une s'appelle primaire et l'autre lycée. Le nombre de tours respectif est N1 et ndeux.
La bobine ou l'enroulement primaire est connecté à une tension alternative (telle qu'une prise électrique domestique, par exemple) sous la forme VP = V1.cos ωt, faisant circuler à l'intérieur un courant alternatif de fréquence ω.
Ce courant crée un champ magnétique qui à son tour provoque un flux magnétique oscillant dans la deuxième bobine ou enroulement, avec une tension secondaire de la forme VS = Vdeux.cos ωt.
Or, il s'avère que le champ magnétique à l'intérieur du noyau de fer est proportionnel à l'inverse du nombre de tours de l'enroulement primaire:
B ∝ 1 / N1
Et il en sera de même VP, la tension aux bornes de l'enroulement primaire, tandis que le fem induit VS dans le second enroulement il est proportionnel, comme on le sait déjà, au nombre de tours Ndeux et aussi à VP.
Donc, en combinant ces proportionnalités, nous avons une relation entre VS Oui VP qui dépend du quotient entre le nombre de tours de chacun, comme suit:
VS = (Ndeux / N1) VP
Ce sont des appareils utilisés dans les banques et les aéroports pour la sécurité. Ils détectent la présence de n'importe quel métal, pas seulement du fer ou du nickel. Ils fonctionnent grâce aux courants induits, grâce à l'utilisation de deux bobines: un émetteur et un récepteur..
Un courant alternatif haute fréquence est passé dans la bobine de l'émetteur, de sorte qu'il génère un champ magnétique alternatif le long de l'axe (voir figure), qui induit un courant dans la bobine de réception, quelque chose de plus ou moins similaire à ce qui se passe avec le transformateur.
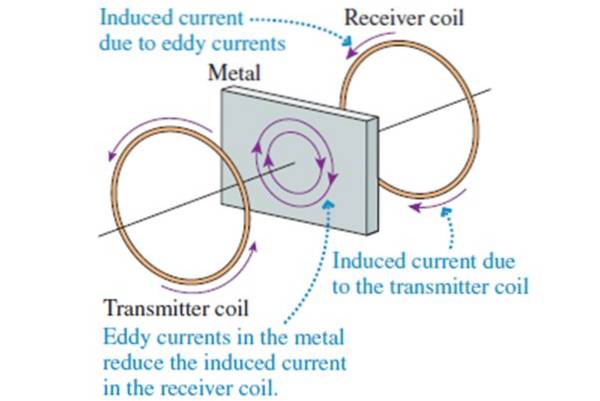
Si un morceau de métal est placé entre les deux bobines, de petits courants induits y apparaissent, appelés courants de Foucault (qui ne peuvent pas circuler dans un isolant). La bobine réceptrice répond aux champs magnétiques de la bobine émettrice et à ceux créés par les courants de Foucault..
Les courants de Foucault tentent de minimiser le flux de champ magnétique dans le morceau de métal. Par conséquent, le champ perçu par la bobine réceptrice diminue lorsqu'une pièce métallique est interposée entre les deux bobines. Lorsque cela se produit, une alarme est déclenchée qui avertit de la présence d'un métal.
Il y a une bobine circulaire de 250 tours de 5 cm de rayon, située perpendiculairement à un champ magnétique de 0,2 T.Déterminer le fem induit si dans un intervalle de temps de 0,1 s, l'amplitude du champ magnétique double et indique la direction du courant, selon la figure suivante:
Nous allons d'abord calculer la magnitude de la force électromotrice induite, puis la direction du courant associé sera indiquée selon le dessin.
N = 250 tours
A = π. Rdeux = p. (5 x 10-deux m)deux = 0,0079 mdeux.
cos θ = cos 0 = 1 (Le vecteur n est pris parallèlement à B)
Puisque le champ magnétique double sa magnitude, nous avons:
En remplaçant ces valeurs dans l'équation de la magnitude de la fem induit:
ε = 250. 0,0079 mdeux . 2 T / s = 3,95 V
Puisque le champ a doublé, le flux de champ magnétique a également doublé, donc un courant induit est créé dans la boucle qui s'oppose à cette augmentation..
Le champ de la figure pointe vers l'écran. Le champ créé par le courant induit doit quitter l'écran, en appliquant la règle du pouce droit, il s'ensuit que le courant induit est dans le sens antihoraire.
Un enroulement carré est composé de 40 spires de 5 cm de chaque côté, qui tournent avec une fréquence de 50 Hz au milieu d'un champ uniforme de magnitude 0,1 T. Initialement, la bobine est perpendiculaire au champ. Quelle sera l'expression de la fem induit?
Des sections précédentes, cette expression a été déduite:
ε = N.B.A. ω. sen ωt
A = (5 x 10-deux m)deux = 0,0025 mdeux
N = 40 tours
ω = 2π.f = 2π.50 Hz = 100p s-1
B = 0,1 T
ε = 40 x 0,1 x 0,0025 x 100π x sin 50.t =p . péché 100π.la télé
Personne n'a encore commenté ce post.