Il a un matrice orthogonale lorsque ladite matrice multipliée par sa transposée aboutit à la matrice d'identité. Si l'inverse d'une matrice est égal à la transposée alors la matrice d'origine est orthogonale.
Les matrices orthogonales ont la caractéristique que le nombre de lignes est égal au nombre de colonnes. De plus, les vecteurs de ligne sont des vecteurs orthogonaux unitaires et les vecteurs de ligne de transposition sont également.
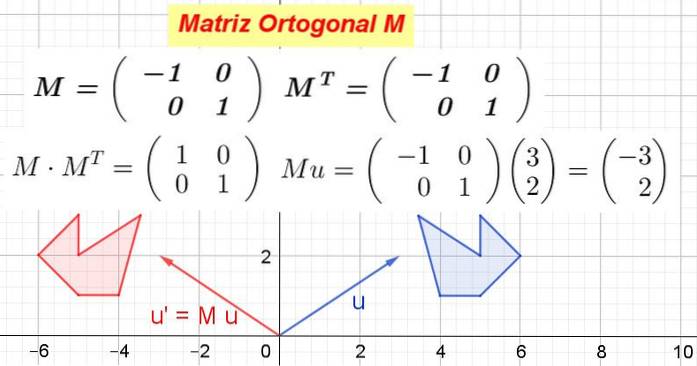
Lorsqu'une matrice orthogonale est multipliée par les vecteurs d'un espace vectoriel, elle produit un transformation isométrique, c'est-à-dire une transformation qui ne change pas les distances et préserve les angles.
Un représentant typique des matrices orthogonales sont les matrices de rotation. Les transformations de matrices orthogonales sur un espace vectoriel sont appelées transformations orthogonales.
Les transformations géométriques de rotation et de réflexion des points représentés par leurs vecteurs cartésiens sont réalisées en appliquant des matrices orthogonales sur les vecteurs originaux pour obtenir les coordonnées des vecteurs transformés. C'est pour cette raison que les matrices orthogonales sont largement utilisées dans le traitement graphique informatique..
Index des articles
Un tableau M est orthogonale si multipliée par sa transposition MT renvoie la matrice d'identité je. De même, le produit de la transposée d'une matrice orthogonale par la matrice d'origine aboutit à la matrice identité:
M MT = MT M = I
En conséquence de l'énoncé précédent, nous avons que la transposée d'une matrice orthogonale est égale à sa matrice inverse:
MT = M-1.
L'ensemble des matrices orthogonales de dimension n x n forment le groupe des orthogonales Au). Et le sous-ensemble de Au) de matrices orthogonales de déterminant +1 forment le Groupe de matrices spéciales unitaires SU (n). Les matrices de groupe Soleil) sont des matrices qui produisent des transformations linéaires de rotation, également appelées groupe de rotations.
Montrons qu'une matrice est orthogonale si, et seulement si, les vecteurs lignes (ou les vecteurs colonnes) sont orthogonaux entre eux et de norme 1.
Supposons que les lignes d'une matrice orthogonale n x n soient n vecteurs orthonormés de dimension n. Si indiqué par v1, vdeux,…., Vn les n vecteurs sont satisfaits:
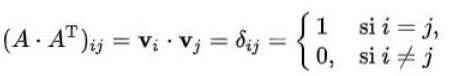
Où il est évident qu'en effet l'ensemble des vecteurs lignes est un ensemble de vecteurs orthogonaux de norme un.
Montrer que la matrice 2 x 2 qui dans sa première ligne a le vecteur v1= (-1 0) et dans sa deuxième ligne le vecteur v2= (0 1) est une matrice orthogonale.
Solution: La matrice est construite M et sa transposition est calculée MT:
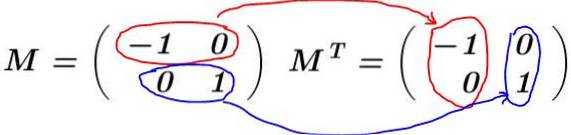
Dans cet exemple, le tableau M il est auto-transposé, c'est-à-dire que la matrice et sa transposée sont identiques. Il multiplie M par sa transposition MT:
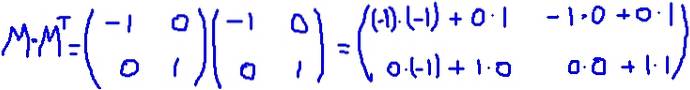
Il est vérifié que M MT est égal à la matrice d'identité:
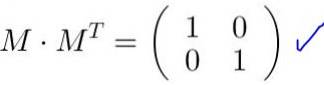
Quand la matrice M est multipliée par les coordonnées d'un vecteur ou d'un point, de nouvelles coordonnées sont obtenues qui correspondent à la transformation que la matrice effectue sur le vecteur ou le point.
La figure 1 montre comment M vecteur de transformation ou alors au ou alors' et aussi comment M transformez le polygone bleu en polygone rouge. Quoi M est orthogonale c'est alors une transformation orthogonale, qui préserve les distances et les angles.
Supposons que vous ayez une matrice 2 x 2 définie dans les réels donnés par l'expression suivante:
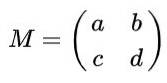
Trouvez les vraies valeurs de à, b, c Oui ré de telle sorte que la matrice M être une matrice orthogonale.
Solution: Par définition, une matrice est orthogonale si multipliée par sa transposée, la matrice d'identité est obtenue. En se rappelant que la matrice transposée est obtenue à partir de l'original, en échangeant des lignes contre des colonnes, l'égalité suivante est obtenue:
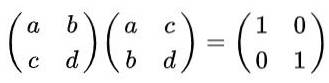
En effectuant la multiplication matricielle, nous avons:
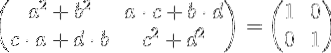
En égalant les éléments de la matrice de gauche avec les éléments de la matrice d'identité de droite, on obtient un système de quatre équations à quatre inconnues a, b, c et d.
Nous proposons les expressions suivantes pour a, b, c et d en termes de rapports trigonométriques sinus et cosinus:
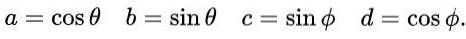
Avec cette proposition et en raison de l'identité trigonométrique fondamentale, les première et troisième équations sont automatiquement satisfaites dans l'égalité des éléments de la matrice. Les troisième et quatrième équations sont les mêmes et en égalité de matrice après avoir substitué les valeurs proposées, cela ressemble à ceci:
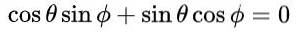
ce qui conduit à la solution suivante:
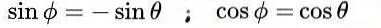
Enfin, les solutions suivantes sont obtenues pour la matrice orthogonale M:
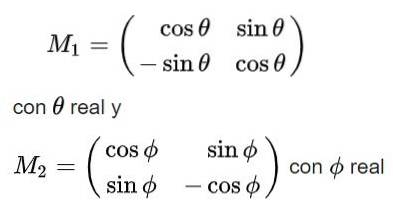
Notez que la première des solutions a le déterminant +1 donc elle appartient au groupe SU (2), tandis que la seconde solution a le déterminant -1 et n'appartient donc pas à ce groupe.
Étant donné la matrice suivante, trouvez les valeurs de a et b pour que nous ayons une matrice orthogonale.
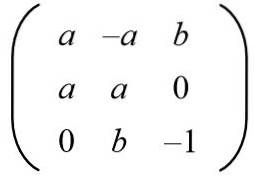
Solution: Pour qu'une matrice donnée soit orthogonale, le produit avec sa transposée doit être la matrice identité. Ensuite, le produit matriciel de la matrice donnée avec sa matrice transposée est réalisé, donnant le résultat suivant:
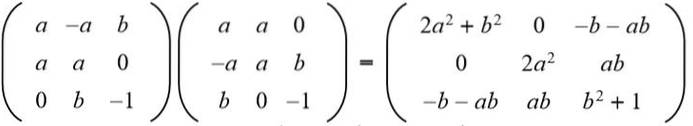
Ensuite, le résultat est assimilé à la matrice d'identité 3 x 3:
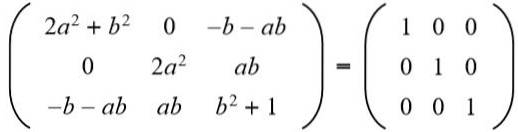
Dans la deuxième ligne, troisième colonne, nous avons (a b = 0), mais à il ne peut pas être nul, car si c'est le cas, l'égalité des éléments de la deuxième ligne et de la deuxième colonne ne serait pas remplie. Alors forcément b = 0. Substituer b pour la valeur 0 on a:
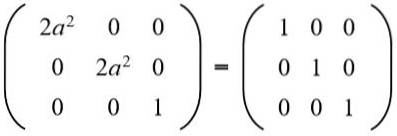
Ensuite, l'équation est résolue: 2a ^ 2 = 1, dont les solutions sont: + ½√2 et -½√2.
Prendre la solution positive pour à la matrice orthogonale suivante est obtenue:
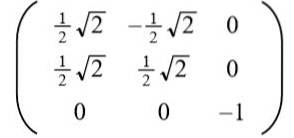
Le lecteur peut facilement vérifier que les vecteurs lignes (ainsi que les vecteurs colonnes) sont orthogonaux et unitaires, c'est-à-dire orthonormés.
Prouvez que la matrice À dont les vecteurs de ligne sont v1 = (0, -1 0), v2 = (1, 0, 0) Oui v3 = (0 0 -1) est une matrice orthogonale. Découvrez également comment les vecteurs de la base canonique sont transformés Je J K aux vecteurs u1, u2 Oui u3.
Solution: Il faut se rappeler que l'élément (i, j) d'une matrice multiplié par sa transposée, est le produit scalaire du vecteur de la ligne (i) par celui de la colonne (j) de la transposée. De plus, ce produit est égal au delta de Kronecker dans le cas où la matrice est orthogonale:
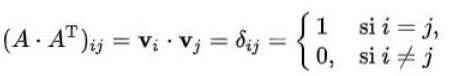
Dans notre cas, cela ressemble à ceci:
v1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1
v2 • v2 = 1 × 1 + 0x0 + 0x0 = 1
v3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1
v1 • v2 = 0x1 + (-1) x0 + 0x0 = 0
v2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0
v2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0
v3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0
v1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0
v3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0
Avec lequel on montre qu'il s'agit d'une matrice orthogonale.
En outre u1 = A i = (0, 1, 0); u2 = A j = (-1, 0, 0) et enfin u3 = A k = (0, 0, -1)
Personne n'a encore commenté ce post.