Modèle atomique de Heisenberg

Quel est le modèle atomique de Heisenberg?

le Modèle atomique de Heisenberg (1927) introduit le principe d'incertitude dans les orbitales électroniques entourant le noyau atomique. L'éminent physicien allemand a jeté les bases de la mécanique quantique pour estimer le comportement des particules subatomiques qui composent un atome.

Le principe d'incertitude de Werner Heisenberg indique qu'il n'est pas possible de connaître avec certitude la position et le moment linéaire d'un électron en même temps. Le même principe s'applique aux variables temps et énergie; c'est-à-dire que si nous avons un indice sur la position de l'électron, nous ne connaîtrons pas l'impulsion linéaire de l'électron, et vice versa.

En bref, il n'est pas possible de prédire simultanément la valeur des deux variables. Ce qui précède n'implique pas qu'aucune des quantités susmentionnées ne puisse être connue avec précision. Tant qu'il est séparé, il n'y a aucun obstacle à l'obtention de la valeur d'intérêt.

Cependant, l'incertitude survient lorsqu'il s'agit de connaître simultanément deux quantités conjuguées, telles que la position et l'impulsion linéaire, et le temps avec l'énergie..

Ce principe découle d'un raisonnement strictement théorique, comme seule explication viable pour justifier des observations scientifiques.

Caractéristiques du modèle atomique de Heisenberg

En mars 1927, Heisenberg publia son ouvrage Sur le contenu perceptif de la cinématique et de la mécanique quantique théorique, où vous avez détaillé le principe d'incertitude ou d'indétermination.

Ce principe, fondamental dans le modèle atomique proposé par Heisenberg, se caractérise par:

• Le principe d'incertitude apparaît comme une explication qui complète les nouvelles théories atomiques sur le comportement des électrons. Malgré l'utilisation d'instruments de mesure de haute précision et sensibilité, l'indétermination est toujours présente dans tout test expérimental.
• En raison du principe d'incertitude, lors de l'analyse de deux variables liées, si vous avez une connaissance précise de l'une d'entre elles, l'incertitude sur la valeur de l'autre variable sera de plus en plus grande..
• L'élan et la position d'un électron ou d'une autre particule subatomique ne peuvent pas être mesurés en même temps.
• La relation entre les deux variables est donnée par une inégalité. Selon Heisenberg, le produit des variations de l'impulsion linéaire et de la position de la particule est toujours supérieur au quotient entre la constante de Plank (6.62606957 (29) × 10 ^{-3. 4} Jules x secondes) et 4π, comme détaillé dans l'expression mathématique suivante:

La légende correspondant à cette expression est la suivante:

∆p: indétermination du moment linéaire.

∆x: indétermination de la position.

h: constante de la planche.

π: nombre pi 3,14.

• Au vu de ce qui précède, le produit des incertitudes a comme limite inférieure le rapport h / 4π, qui est une valeur constante. Par conséquent, si l'une des grandeurs tend vers zéro, l'autre doit augmenter dans la même proportion.
• Cette relation est valable pour toutes les paires de quantités canoniques conjuguées. Par exemple: le principe d'incertitude de Heisenberg est parfaitement applicable au couple énergie-temps, comme détaillé ci-dessous:

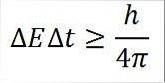
Dans cette expression:

∆E: indétermination de l'énergie.

∆t: indétermination du temps.

h: constante de la planche.

π: nombre pi 3,14.

• De ce modèle, il s'ensuit que le déterminisme causal absolu dans les variables canoniques conjuguées est impossible, car pour établir cette relation, il faut avoir des connaissances sur les valeurs initiales des variables de l'étude..
• Par conséquent, le modèle de Heisenberg est basé sur des formulations probabilistes, en raison du caractère aléatoire qui existe entre les variables aux niveaux subatomiques..

Tests expérimentaux

Le principe d'incertitude de Heisenberg apparaît comme la seule explication possible des tests expérimentaux qui ont eu lieu au cours des trois premières décennies du 21e siècle..

Avant qu'Heisenberg n'énonce le principe d'incertitude, les préceptes en vigueur à l'époque suggéraient que les variables moment linéaire, position, moment cinétique, temps, énergie, entre autres, pour les particules subatomiques étaient définies de manière opérationnelle..

Cela signifiait qu'ils étaient traités comme s'ils étaient de la physique classique; c'est-à-dire qu'une valeur initiale a été mesurée et la valeur finale a été estimée selon la procédure préétablie.

Cela impliquait de définir un référentiel de mesures, l'instrument de mesure et la manière d'utiliser ledit instrument, conformément à la méthode scientifique..

En conséquence, les variables décrites par les particules subatomiques devaient se comporter de manière déterministe. Autrement dit, son comportement devait être prédit avec exactitude et précision..

Cependant, à chaque fois qu'un test de cette nature était réalisé, il était impossible d'obtenir la valeur théoriquement estimée dans la mesure.. 

Les mesures ont été déformées en raison des conditions naturelles de l'expérience, et le résultat obtenu n'a pas été utile pour enrichir la théorie atomique.

Exemple

Par exemple: s'il s'agit de mesurer la vitesse et la position d'un électron, le montage de l'expérience doit envisager la collision d'un photon de lumière avec l'électron.

Cette collision induit une variation de la vitesse et de la position intrinsèque de l'électron, avec laquelle l'objet de la mesure est altéré par les conditions expérimentales..

Par conséquent, le chercheur encourage la survenue d'une erreur expérimentale inévitable, malgré l'exactitude et la précision des instruments utilisés..

Mécanique quantique autre que la mécanique classique

En plus de ce qui précède, le principe d'indétermination de Heisenberg stipule que, par définition, la mécanique quantique fonctionne différemment de la mécanique classique.

Par conséquent, on suppose que la connaissance précise des mesures au niveau subatomique est limitée par la ligne fine qui sépare la mécanique classique et quantique..

Limitations du modèle Heisenberg

Malgré l'explication de l'indétermination des particules subatomiques et l'établissement des différences entre la mécanique classique et quantique, le modèle atomique de Heisenberg n'établit pas une seule équation pour expliquer le caractère aléatoire de ce type de phénomènes..

De plus, le fait que la relation s'établisse à travers une inégalité implique que la gamme des possibilités pour le produit de deux variables canoniques conjuguées est indéterminée. Par conséquent, l'incertitude inhérente aux processus subatomiques est importante..

Articles d'intérêt

Modèle atomique de Schrödinger.

Modèle Atomic de Broglie.

Modèle atomique de Chadwick.

Le modèle atomique de Perrin.

Le modèle atomique de Thomson.

Modèle atomique de Dalton.

Modèle atomique de Dirac Jordan.

Modèle atomique de Démocrite.

Modèle atomique de Leucippe.

Modèle atomique de Bohr.

Modèle atomique de Sommerfeld.

Modèle atomique actuel.

Les références

1. Beyler, R. (1998). Werner Heisenberg. Encyclopædia Britannica, Inc. Récupéré de: britannica.com
2. Le principe d'incertitude de Heisenberg (s.f.). Récupéré de: hiru.eus
3. García, J. (2012). Principe d'incertitude d'Heisenberg. Récupéré de: hiberus.com
4. Modèles atomiques (s.f.). Université nationale autonome du Mexique. Mexico DF, Mexique. Récupéré de: asesorias.cuautitlan2.unam.mx
5. Werner Heisenberg (s.f.). Récupéré de: the-history-of-the-atom.wikispaces.com
6. Wikipédia, l'encyclopédie libre (2018). La constante de la planche. Récupéré de: es.wikipedia.org
7. Wikipédia, l'encyclopédie libre (2018). Relation d'indétermination de Heisenberg. Récupéré de: es.wikipedia.org