le couple, le couple ou le moment d'une force est la capacité d'une force à provoquer un virage. Etymologiquement, il reçoit le nom de torque comme une dérivation du mot anglais couple, du latin torquere (tourner).
Le couple (par rapport à un point donné) est la grandeur physique qui résulte de la réalisation du produit vectoriel entre les vecteurs de position du point où la force est appliquée et celui de la force exercée (dans l'ordre indiqué). Ce moment dépend de trois éléments principaux.
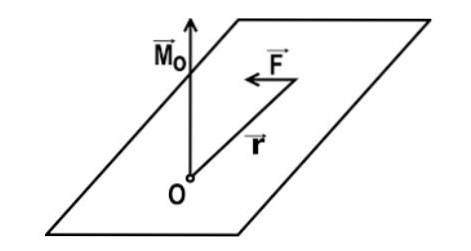
Le premier de ces éléments est l'amplitude de la force appliquée, le second est la distance entre le point où il est appliqué et le point par rapport auquel le corps tourne (également appelé bras de levier), et le troisième élément est l'angle d'application de ladite force.
Plus la force est élevée, plus la rotation est importante. Il en va de même avec le bras de levier: plus la distance entre le point où la force est appliquée et le point par rapport auquel elle produit le virage est grande, plus elle sera grande..
Bien sûr, le couple est d'un intérêt particulier dans la construction et l'industrie, ainsi qu'il est présent dans d'innombrables applications pour la maison, comme lorsqu'un écrou est serré avec une clé..
Index des articles
L'expression mathématique du couple d'une force par rapport à un point O est donnée par: M = r x F
Dans cette expression r est le vecteur qui joint le point de O au point P d'application de la force, et F est le vecteur de la force appliquée.
Les unités de mesure du moment sont N ∙ m, qui bien que dimensionnellement équivalentes au Joule (J), ont une signification différente et ne doivent pas être confondues.
Par conséquent, le module du couple prend la valeur donnée par l'expression suivante:
M = r ∙ F ∙ sin α
Dans cette expression, α est l'angle entre le vecteur de force et le vecteur r ou bras de levier. Le couple est considéré comme positif si le corps tourne dans le sens antihoraire; au contraire, il est négatif lorsqu'il tourne dans le sens des aiguilles d'une montre.
Comme déjà mentionné ci-dessus, l'unité de mesure du couple résulte du produit d'une unité de force et d'une unité de distance. Plus précisément, le Système international d'unités utilise le newton mètre dont le symbole est N • m.
Au niveau dimensionnel, le newton mètre peut sembler équivalent au joule; cependant, en aucun cas, juillet ne doit être utilisé pour exprimer des moments. Le joule est une unité de mesure d'œuvres ou d'énergies qui, d'un point de vue conceptuel, sont très différentes des moments de torsion.
De la même manière, le moment de torsion a un caractère vectoriel, qui est à la fois le travail scalaire et l'énergie.
De ce qui a été vu, il s'ensuit que le couple d'une force par rapport à un point représente la capacité d'une force ou d'un ensemble de forces à modifier la rotation dudit corps autour d'un axe passant par le point..
Par conséquent, le moment de torsion génère une accélération angulaire sur le corps et est une grandeur d'un caractère vectoriel (il est donc défini à partir d'un module, d'une direction et d'un sens) qui est présent dans les mécanismes qui ont subi une torsion ou une flexion..
Le couple sera nul si le vecteur force et le vecteur r ont la même direction, puisque dans ce cas la valeur de sin α sera nulle.
Etant donné un certain corps sur lequel agit une série de forces, si les forces appliquées agissent dans le même plan, le couple résultant de l'application de toutes ces forces; est la somme des moments de torsion résultant de chaque force. Par conséquent, il est vrai que:
MT = ∑ M = M1 + Mdeux + M3 +...
Bien entendu, il faut prendre en compte le critère de signe pour les moments de torsion, comme expliqué ci-dessus.
Le couple est présent dans des applications aussi quotidiennes que le serrage d'un écrou avec une clé, ou l'ouverture ou la fermeture d'un robinet ou d'une porte.
Cependant, ses applications vont beaucoup plus loin; le couple se retrouve également dans les axes de la machine ou à la suite des efforts auxquels sont soumises les poutres. Par conséquent, ses applications dans l'industrie et la mécanique sont nombreuses et variées..
Voici quelques exercices pour faciliter la compréhension de ce qui précède.
Compte tenu de la figure suivante dans laquelle les distances entre le point O et les points A et B sont respectivement de 10 cm et 20 cm:
a) Calculer la valeur du module du couple par rapport au point O si une force de 20 N est appliquée au point A.
b) Calculez quelle doit être la valeur de la force appliquée en B pour obtenir le même couple que celui obtenu dans la section précédente.
En premier lieu, il est pratique de transférer les données vers des unités du système international.
rÀ = 0,1 m
rB = 0,2 m
a) Pour calculer le module du couple, nous utilisons la formule suivante:
M = r ∙ F ∙ sin α = 0,1 ∙ 20 ∙ 1 = 2 N ∙ m
b) Pour déterminer la force demandée, procédez de la même manière:
M = r ∙ F ∙ sin α = 0,2 ∙ F ∙ 1 = 2 N ∙ m
En résolvant pour F, on obtient que:
F = 10 N
Une femme exerce une force de 20 N au bout d'une clé de 30 cm de long. Si l'angle de la force avec la poignée de la clé est de 30 °, quel est le couple sur l'écrou??
La formule suivante est appliquée et l'opération est effectuée:
M = r ∙ F ∙ sin α = 0,3 ∙ 20 ∙ 0,5 = 3 N ∙ m
Personne n'a encore commenté ce post.