Une particule a mouvement circulaire uniforme (M.C.U.) lorsque sa trajectoire est une circonférence et qu'il la parcourt également à vitesse constante. De nombreux objets tels que des pièces de machines et de moteurs, par exemple, ont ce type de mouvement, parmi lesquels se distinguent les disques durs d'ordinateur, les pales de ventilateur, les arbres et bien d'autres choses..
Le mouvement circulaire uniforme est également une bonne approximation pour le mouvement de certains corps célestes tels que la Terre. En fait, l'orbite terrestre est elliptique, comme l'indiquent les lois de Kepler. Cependant, l'excentricité de l'orbite est petite et en première approximation, elle peut être considérée comme circulaire, ce qui simplifie certains calculs, comme trouver la vitesse de la Terre lorsqu'elle se déplace autour du Soleil..
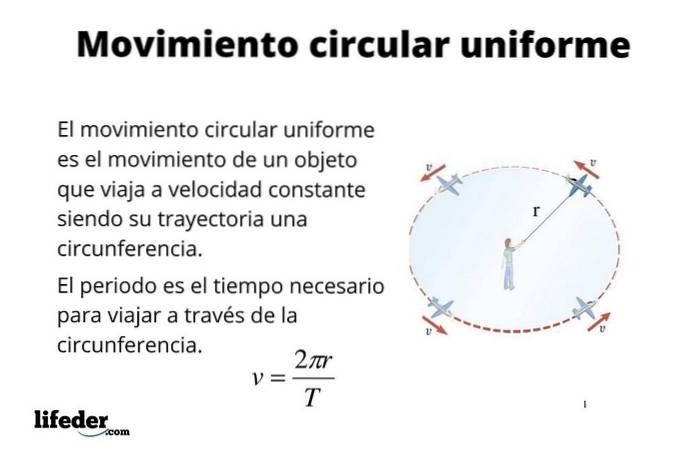
Pour décrire le mouvement circulaire uniforme, les mêmes paramètres sont utilisés que dans le mouvement rectiligne, à savoir: la position, le déplacement, le temps, la vitesse et l'accélération..
Accélération? Oui, en effet, le mouvement circulaire uniforme est accéléré, même si sa vitesse v être constant. C'est parce que la vitesse v, qui est un vecteur et c'est pourquoi il est en gras, changeant continuellement sa direction lorsque l'objet ou la particule tourne. Tout changement dans v est produit par une accélération qui, comme on le verra, est dirigée vers le centre de la trajectoire circulaire.
Un mouvement circulaire uniforme est un mouvement dans le plan xy, c'est donc un mouvement en deux dimensions. Cependant, il est possible de l'exprimer plus confortablement au moyen de l'angle θ que balaie la particule, mesuré par rapport à l'axe horizontal ou à un autre axe de référence approprié..
Même s'il s'agit d'un objet étendu, ses particules balaient toujours le même angle, même si elles ont des coordonnées différentes. (x, y).
Index des articles
Les caractéristiques du mouvement circulaire uniforme peuvent être résumées comme suit:
-La trajectoire est une circonférence, donc c'est un mouvement dans le plan.
-La rapidité v est constante, mais la vitesse v non, car il change continuellement de direction et de direction pour s'adapter au virage du mobile.
-Le vecteur vitesse v est toujours tangent à la circonférence et perpendiculaire à la direction radiale.
-La vitesse angulaire ω est constante.
-En dépit d'être uniforme, il y a une accélération pour expliquer ces changements dans la direction de la vitesse. Cette accélération est l'accélération centripète.
-L'accélération et la vitesse centripètes sont perpendiculaires l'une à l'autre.
-C'est un mouvement périodique ou répétitif, donc les amplitudes de période et de fréquence sont définies pour lui.
Dans ce schéma, il y a une particule P tournant dans le sens antihoraire avec MCU, selon la direction et le sens du vecteur vitesse v dessiné.
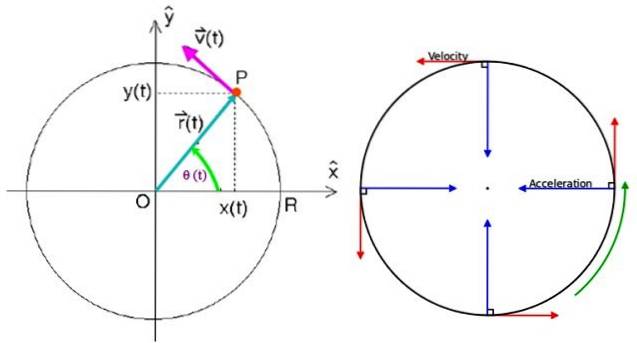
Pour spécifier le vecteur de position, il est nécessaire d'avoir un point de référence et le point idéal est le centre de la circonférence O qui coïncide avec le centre du système de coordonnées cartésien dans le plan xy.
Il est noté r (t) et est dirigé de l'origine vers le point P où se trouve la particule. A un instant t donné, en coordonnées cartésiennes, il s'écrit:
r (t) = x (t) je + et T) j
Où je Oui j sont les vecteurs unitaires perpendiculaires aux directions X et Oui respectivement. À partir du graphique, on peut voir que le module vectoriel r (t) vaut toujours R, le rayon de la circonférence. Si θ est l'angle formé r avec l'axe horizontal, la position est également égale à:
r (t) = [Rcos θ(t)] je +[Rsen θ(t)] j
L'angle qu'il forme r (t) avec l'axe horizontal est un angle central et sa valeur est:
θ = s / R
Où s est l'arc de circonférence parcouru et R le rayon. Ledit angle θ est une fonction du temps, donc il peut être écrit θ = θ (t), appel position angulaire.
La vitesse étant constante, la particule décrit des angles égaux en temps égaux et par analogie avec le mouvement rectiligne uniforme, il s'écrit:
θ = θ (t) = θou alors + ωt
Ici θou alors est l'angle initial mesuré en radians par rapport à l'axe de référence, il peut être égal à 0 ou à n'importe quelle valeur et ω est la vitesse angulaire.
La vitesse angulaire est la première dérivée de la position angulaire et est notée ω. Sa valeur est constante pour un mouvement circulaire uniforme, car des angles égaux sont balayés en des temps égaux. En d'autres termes:
Les unités de vitesse linéaire en mouvement circulaire uniforme sont les mêmes que pour le mouvement linéaire: m / s (dans le système international SI), km / h, cm / s et autres..
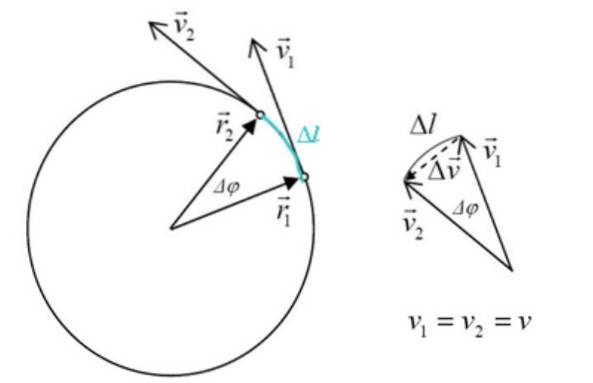
Dans la figure ci-dessous, il y a une particule se déplaçant dans le sens des aiguilles d'une montre autour de la circonférence avec une vitesse constante. Cela signifie que le vecteur vitesse a toujours le même module, mais qu'il change de direction pour s'adapter à la circonférence.
Tout changement de vitesse entraîne une accélération, qui par définition est:
Le triangle formé par vdeux, v1 et Δv est similaire au triangle des côtés rdeux, r1 et Δl, où Δφ est l'angle central. Les magnitudes de rdeux Oui r1 ce sont les mêmes, donc:
rdeux = r1 = r
Ensuite, des deux triangles, nous avons ces relations pour l'angle:
Δφ = Δr / r; Δφ = Δv / v
Le caractère gras n'est pas nécessaire, car la mesure de l'angle dépend des grandeurs de ces vecteurs. En faisant correspondre les expressions précédentes, il s'ensuit que:
Le mouvement circulaire étant répétitif, la période est définie T le même que le temps nécessaire au mobile pour effectuer un tour complet. Puisque la longueur de la circonférence du rayon R est de 2πR, l'angle balayé en radians sur le tour complet est de 2π radians et cela prend le temps T, la vitesse angulaire est:
ω = 2π / T
T = 2π / ω
La période de mouvement circulaire uniforme est mesurée en secondes dans le système international.
De son côté, la fréquence F est le nombre de tours par unité de temps et est l'inverse ou l'inverse de la période:
f = n / t = 1 / T
L'unité de fréquence dans le système international est s-1.
De nombreux objets tournent pour produire divers effets: roues, disques et turbines. Une fois la vitesse de fonctionnement atteinte, la rotation s'effectue généralement à vitesse constante. Le mouvement circulaire est si courant dans la vie quotidienne que vous n'y pensez presque jamais, alors voici quelques exemples proches qui l'illustrent très bien:
La Terre et les autres planètes du système solaire se déplacent selon des trajectoires elliptiques de petite excentricité, sauf Mercure, ce qui signifie qu'en première approximation, on peut supposer que leur mouvement est circulaire uniforme.
Avec cela, vous avez une bonne idée de la vitesse de translation autour du Soleil, puisque dans le cas de la Terre, la période du mouvement est connue: un an ou 365 jours..
Les particules qui tournent sur le bord d'un vieux tourne-disque ou la lame d'un ventilateur, suivent un mouvement circulaire uniforme, une fois que l'appareil atteint sa vitesse de lecture.
Le télescope spatial Hubble fait le tour de la Terre à environ 7550 m / s.
Les machines à laver effectuent un processus d'essorage pour presser les vêtements, qui consiste à faire tourner le tambour du conteneur à grande vitesse. Les séchoirs tournent également pendant un certain temps selon un mouvement circulaire uniforme..
La centrifugation est également utilisée dans les laboratoires pour séparer des composés, par exemple, et ainsi séparer leurs constituants par différence de densités. Chaque fois que nous parlons de centrifugation, il y a un mouvement circulaire qui est uniforme, au moins pour un temps.
De nombreux arroseurs de jardin tournent à une vitesse constante pour que le sol soit arrosé uniformément..
Dans le lancer du marteau par exemple, qui est une discipline olympique, l'athlète fait tourner une balle en métal avec force à l'aide d'un câble en acier attaché à la poignée. L'objectif est d'envoyer le ballon le plus loin possible, mais sans quitter une certaine zone.
Une particule se déplace sur une circonférence de rayon 2m avec une vitesse constante v = 8 m / s, dans le sens antihoraire. Au départ, la particule était en r = +2 j m. Calculer:
a) La vitesse angulaire ω
b) Sa position angulaire θ (t)
c) La période de mouvement
d) Accélération centripète.
e) Position de la particule après avoir passé t = π / 4 s
De la formule v = Rω, il s'ensuit que:
ω = v / R = (8 m / s) / 2m = 4rad ∙ s-1
En prenant l'axe x positif comme axe de référence, la particule est initialement à 90º = π / 2 radians par rapport audit axe, puisque l'énoncé dit que la position initiale est +2 j m, c'est-à-dire que la particule est à y = 2m lorsque le mouvement commence à suivre.
θ = θ (t) = θou alors + ωt = π / 2 + 4t
T = 2π / ω = 2π / 4 s = 0,5 π s
a = vdeux / R = (8 m / s)deux / 2 m = 32 m / sdeux
θ (t) = π / 2 + 4t → θ (π / 4) = π / 2 + 4 ∙ (π / 4) = 3π / 2 radians
Cela signifie qu'après ce temps, la particule est dans la position y = -2m j. Cela a du sens car t = π / 4 s est la moitié de la période, donc la particule a parcouru un angle de 180 ° dans le sens antihoraire à partir de sa position initiale et elle doit être juste dans la position opposée.
Personne n'a encore commenté ce post.