
Mouvement pendulaire
Quel est le mouvement du pendule?
le mouvement de pendule C'est un mouvement de va-et-vient effectué par un objet plus ou moins lourd, appelé pendule, suspendu par une corde ou tige légère, fixée à son autre extrémité.
Le pendule reçoit une impulsion initiale et est autorisé à osciller, de cette manière l'objet décrit des arcs d'avant en arrière. C'est le principe de la façon dont les horloges à pendule, les balançoires, les fauteuils à bascule et métronomes pendule, utilisé pour marquer les temps en musique.
On dit que vers 1581, Galileo Galilei a observé l'oscillation d'une lampe dans la cathédrale de Pise, observant que, bien que l'amplitude de l'oscillation du candélabre diminuait en raison du frottement avec l'air, pas la durée du cycle de la lampe..
Cela a attiré l'attention de Galilée, qui a décidé de poursuivre l'étude et a déterminé que la période du pendule ne dépendait pas de la masse, mais de la racine carrée de la longueur de la corde, comme on le verra plus tard..
Caractéristiques du mouvement pendulaire
Un pendule est très facile à construire, car il suffit d'un fil à plomb suspendu à un fil de coton et tenu par l'autre extrémité avec les doigts ou en le fixant à un support comme un clou..
Après la petite impulsion initiale, le poids est chargé de maintenir le pendule en oscillation, bien que le frottement diminue l'amplitude du mouvement, jusqu'à ce qu'il cesse finalement complètement..
La principale caractéristique du mouvement pendulaire est d'être répétitif, car il s'agit d'un mouvement de va-et-vient. Or, pour faciliter son étude, il convient de faire quelques simplifications pour se concentrer sur un modèle plus simple, appelé le pendule simple.
Le pendule simple

C'est un système idéal qui consiste en un fil à plomb, considéré comme une masse ponctuelle m, attaché à une corde légère et inextensible de longueur L. Les caractéristiques de ce système sont:
- Avoir un mouvement répétitif et périodique, consistant à aller et venir sur un arc de circonférence de rayon égal à L.
- Ne prend pas en compte les frottements.
- L'amplitude de mouvement est petite (< 5º).
- La période est indépendante de la masse m, et dépend uniquement de la longueur L pendule.
Formules et équations
Ce qui suit est un diagramme du pendule simple, sur lequel agissent deux forces: le poids P de magnitude mg, qui est dirigée verticalement vers le bas et la tension T Sur la corde. La friction n'est pas prise en compte.
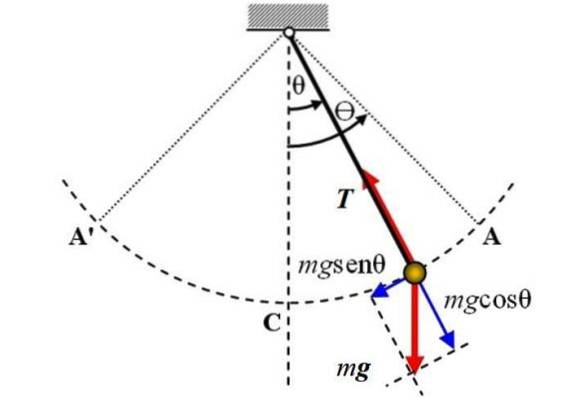
L'axe de référence est l'axe vertical et coïncide avec la position θ = 0, à partir de là le déplacement angulaire θ est mesuré, soit dans un sens soit dans un autre. Le signe + peut être attribué au décalage droit dans la figure.
Pour étudier le mouvement du pendule, un système de coordonnées avec l'origine au pendule lui-même est choisi. Ce système a une coordonnée tangentielle à l'arc de circonférence A'CA décrit par le pendule, ainsi qu'une coordonnée radiale, dirigée vers le centre de la trajectoire..
À l'instant indiqué sur la figure, le pendule se déplace vers la droite, mais la composante tangentielle de la gravité, appelée Ft, est responsable de le faire revenir. On peut voir sur la figure que ce composant a la direction opposée au mouvement.
En ce qui concerne la tension dans la corde, elle est équilibrée avec la composante du poids mgcosθ.

Déplacement angulaire
Il faut exprimer l'équation en termes d'une seule variable, en se rappelant que le déplacement angulaire θ et l'arc parcouru sont liés par l'équation:
s = L.θ
La masse s'annule des deux côtés et si l'amplitude est petite, l'angle θ aussi, donc l'approximation suivante est valide:
sen θ ≈ θ
Avec cela, l'équation différentielle suivante est obtenue pour la variable θ (t):


Cette équation est très facile à résoudre, car sa solution est une fonction dont la dérivée seconde est la fonction elle-même. Il existe trois alternatives: un cosinus, un sinus ou une exponentielle. La fonction cosinus est choisie pour le déplacement angulaire θ (t), car il s'agit d'une fonction bien connue et facile à manipuler.
Le lecteur peut vérifier, en différenciant deux fois, que la fonction suivante satisfait l'équation différentielle:
θ (t) = θm cos (ωt + φ)
Où θm est l'angle maximal de déplacement du pendule par rapport à la verticale et la fréquence angulaire ω est:

Équation de la période
La période T du mouvement est le temps qu'il faut pour exécuter un cycle et est définie comme:

Remplacer ω:

Comme indiqué ci-dessus, la période ne dépend pas de la masse du pendule, mais uniquement de sa longueur..
Exemples de mouvement pendulaire
Mesure de la fréquence cardiaque
Galileo a eu l'idée de mesurer la fréquence cardiaque des personnes, d'ajuster la longueur du pendule pour faire coïncider la période avec les battements du cœur d'une personne..
L'horloge à pendule
C'est sans aucun doute l'un des exemples les plus connus de mouvement pendulaire. La fabrication d'horloges à pendule concerne autant la science que l'art. Le physicien néerlandais Christian Huygens (1629-1695) a développé la première horloge à pendule en 1656, sur la base de l'étude réalisée il y a des années par Galileo.
Pendule de Foucault

C'est un pendule quelque peu différent de celui décrit ci-dessus, car il est capable de tourner dans n'importe quel plan vertical. Il a été créé par le physicien français Léon Foucault (1819-1868) et est utilisé pour visualiser la rotation de la Terre.
Exercice résolu
Un pendule simple passe toutes les 0,5 s par la position d'équilibre. Quelle est la longueur du fil?
Solution
Puisque la période est le temps qu'il faut pour terminer un cycle complet, dans lequel il passe deux fois par la position d'équilibre: l'un va et l'autre en arrière, alors:
T = 2 × 0,5 s = 1 s
De:

La longueur L du fil est effacée:

Le fil mesure 0,25 m ou 25 cm de long.
Les références
- Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 2. Dynamique. Edité par Douglas Figueroa (USB).
- Giambattista, A. 2010. Physique. 2ème. Ed. McGraw Hill.
- Giancoli, D. 2006. Physique: principes avec applications. 6e. Salle des Prentices Ed.
- Katz, D. 2013. Physique pour les scientifiques et les ingénieurs. Fondations et connexions. Apprentissage Cengage.
- Knight, R. 2017. Physique pour les scientifiques et l'ingénierie: une approche stratégique. Pearson.



Personne n'a encore commenté ce post.