
Méthode Euler à quoi ça sert, procédure et exercices
le Méthode d'Euler est la plus basique et la plus simple des procédures utilisées pour trouver des solutions numériques approximatives à une équation différentielle ordinaire du premier ordre, à condition que sa condition initiale soit connue.
Une équation différentielle ordinaire (ODE) est l'équation qui relie une fonction inconnue d'une seule variable indépendante à ses dérivées.
Si la plus grande dérivée qui apparaît dans l'équation est de degré un, alors c'est une équation différentielle ordinaire du premier degré.
La façon la plus générale d'écrire une équation du premier degré est:

x = x0
y = y0
Index des articles
- 1 Quelle est la méthode d'Euler?
- 2 exercices résolus
- 2.1 Exercice 1
- 2.2 Exercice 2
- 2.3 Exercice 3
- 3 Dynamique de Newton et méthode d'Euler
- 3.1 Exercice 4
- 4 Exercices proposés pour la maison
- 4.1 Exercice 1
- 4.2 Exercice 2
- 5 Références
Quelle est la méthode d'Euler?
L'idée de la méthode d'Euler est de trouver une solution numérique à l'équation différentielle dans l'intervalle entre X0 et XF .
Premièrement, l'intervalle est discrétisé en n + 1 points:
X0, X1, Xdeux, X3..., Xn
Qui sont obtenus comme ceci:
Xje= x0+ih
Où h est la largeur ou le pas des sous-intervalles:

Avec la condition initiale, alors il est également possible de connaître la dérivée au début:
y '(xou alors) = f (xou alors, Ouiou alors)
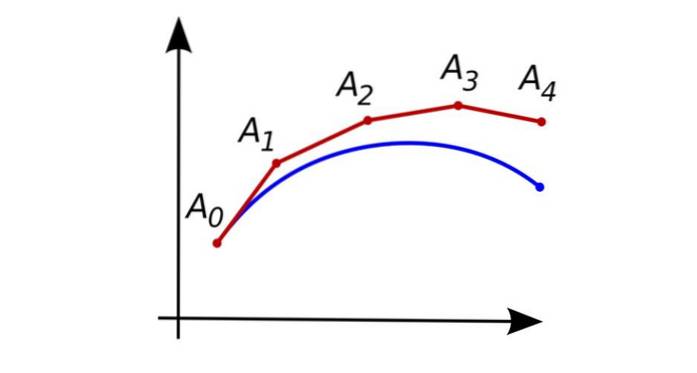
Cette dérivée représente la pente de la tangente à la courbe de la fonction y (x) précisément au point:
Ao = (xou alors, Ouiou alors)
Ensuite, une prédiction approximative de la valeur de la fonction y (x) est faite au point suivant:
y (x1) ≈ et1
Oui1 = Ouiou alors +(X1- Xou alors) f (xou alors, Ouiou alors) = etou alors + h f (xou alors, Ouiou alors)
On a alors obtenu le point approximatif suivant de la solution, qui correspondrait à:
À1 = (x1, Oui1)
La procédure est répétée pour obtenir les points successifs
Àdeux, À3..., Xn
Dans la figure présentée au début, la courbe bleue représente la solution exacte de l'équation différentielle, et la rouge représente les points approximatifs successifs obtenus par la procédure d'Euler.
Exercices résolus
Exercice 1
je) Soit l'équation différentielle:

Avec la condition initiale x = a = 0; Ouià= 1
En utilisant la méthode d'Euler, obtenez une solution approximative de Oui dans la coordonnée X = b = 0,5, en subdivisant l'intervalle [a, b] en n = 5 parties.
Solution

Les résultats numériques sont résumés comme suit:

D'où il est conclu que la solution Y pour la valeur 0,5 est 1,4851.
Remarque: pour effectuer les calculs, Studio Smath, libre d'utiliser le programme gratuit.
Exercice 2
II) En continuant avec l'équation différentielle de l'exercice I), trouvez la solution exacte et comparez-la au résultat obtenu par la méthode d'Euler. Trouvez l'erreur ou la différence entre le résultat exact et approximatif.
Solution

La solution exacte n'est pas très difficile à trouver. La dérivée de la fonction sin (x) est connue pour être la fonction cos (x). Par conséquent, la solution y (x) sera:
y (x) = sin x + C
Pour que la condition initiale soit satisfaite et (0) = 1, la constante C doit être égale à 1. Le résultat exact est alors comparé à l'approximatif:
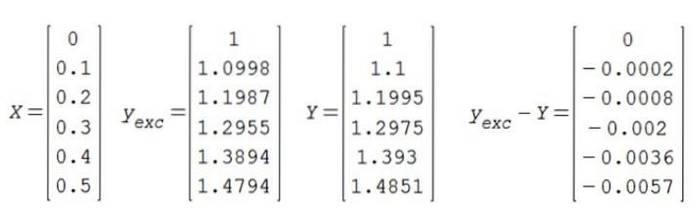
On en conclut que dans l'intervalle calculé, l'approximation a trois chiffres significatifs de précision.
Exercice 3
III) Considérons l'équation différentielle et ses conditions initiales données ci-dessous:
y '(x) = - ydeux
Avec la condition initiale x0 = 0; Oui0 = 1
Utilisez la méthode d'Euler pour trouver des valeurs approximatives de la solution y (x) dans l'intervalle x = [0, 1,5]. Utiliser l'étape h = 0,1.
Solution
La méthode d'Euler est très appropriée pour être utilisée avec une feuille de calcul. Dans ce cas, nous utiliserons la feuille de calcul de géogèbre, un programme gratuit et gratuit.
La feuille de calcul de la figure montre trois colonnes (A, B, C) la première est la variable X , la deuxième colonne représente la variable Oui, et la troisième colonne le dérivé Y '.
La ligne 2 contient les valeurs initiales de X, Oui, Y ' .
Le pas de valeur 0,1 a été placé dans la cellule de position absolue ($ D $ 4).
La valeur initiale de y0 est dans la cellule B2 et y1 est dans la cellule B3. Pour calculer y1 la formule est utilisée:
Oui1 = Ouiou alors +(X1- Xou alors) f (xou alors, Ouiou alors) = etou alors + h f (xou alors, Ouiou alors)
Cette formule de feuille de calcul serait le numéro B3: = B2 + $ D 4 $ * C3.
De même, y2 serait dans la cellule B4 et sa formule est indiquée dans la figure suivante:
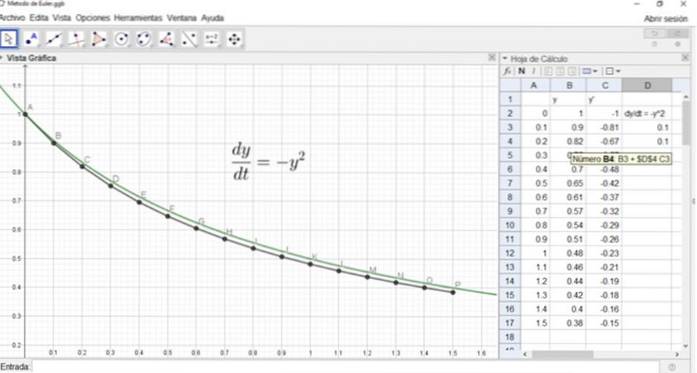
La figure montre également le graphique de la solution exacte, et les points A, B,…, P de la solution approchée par la méthode d'Euler.
Dynamique newtonienne et méthode d'Euler
La dynamique classique a été développée par Isaac Newton (1643 - 1727). La motivation originale de Leonard Euler (1707 - 1783) pour développer sa méthode, était précisément de résoudre l'équation de la deuxième loi de Newton dans diverses situations physiques..
La deuxième loi de Newton est généralement exprimée sous la forme d'une équation différentielle du deuxième degré:

Où X représente la position d'un objet à l'instant t. Ledit objet a une masse m et est soumis à une force F. La fonction F est lié à la force et à la masse comme suit:


Pour appliquer la méthode d'Euler, les valeurs initiales du temps sont nécessaires t, rapidité v et position X.
Le tableau suivant explique comment à partir des valeurs initiales t1, v1, x1 une approximation de la vitesse v2 et de la position x2 peut être obtenue, à l'instant t2 = t1 + Δt, où Δt représente une petite augmentation et correspond au pas dans la méthode d'Euler.

Exercice 4
IV) L'un des problèmes fondamentaux de la mécanique est celui d'un bloc de masse M lié à un ressort (ou ressort) de constante élastique K.
La deuxième loi de Newton pour ce problème ressemblerait à ceci:
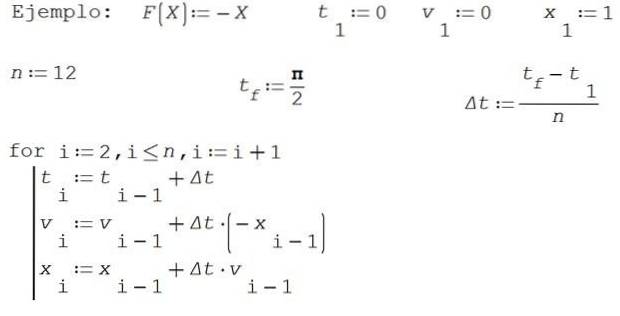
Dans cet exemple, pour simplifier, nous prendrons M = 1 et K = 1. Trouver des solutions approximatives pour positionner X et vitesse v par la méthode d'Euler sur l'intervalle de temps [0, π / 2] en subdivisant l'intervalle en 12 parties.
Prendre 0 comme instant initial, la vitesse initiale 0 et la position initiale 1.
Solution
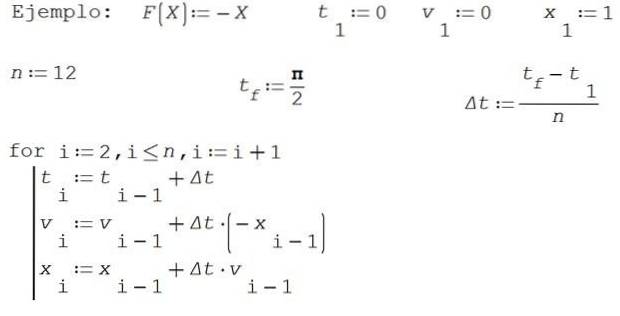
Les résultats numériques sont présentés dans le tableau suivant:
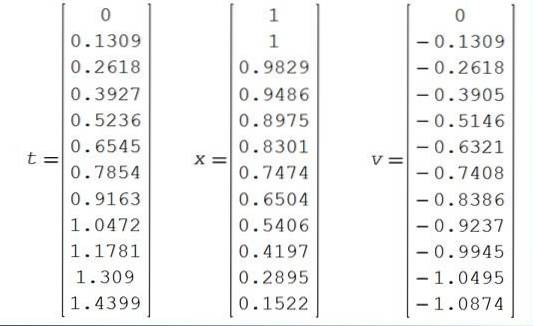
Les graphiques de la position et de la vitesse entre les instants 0 et 1,44 sont également représentés..
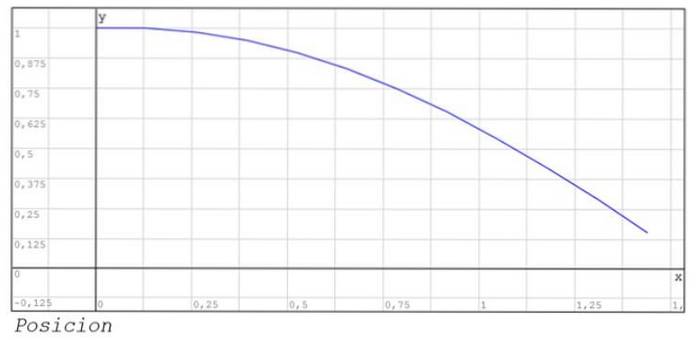
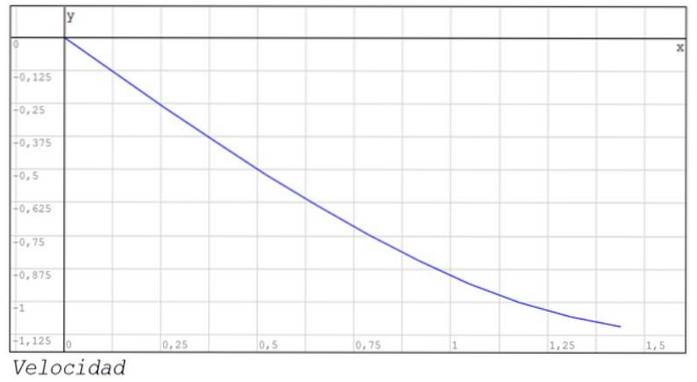
Exercices proposés pour la maison
Exercice 1
Utilisez une feuille de calcul pour déterminer une solution approximative en utilisant la méthode d'Euler pour l'équation différentielle:
y '= - Exp (-y) avec les conditions initiales x = 0, y = -1 dans l'intervalle x = [0, 1]
Commencez par un pas de 0,1. Tracez le résultat.
Exercice 2
À l'aide d'une feuille de calcul, trouvez des solutions numériques à l'équation quadratique suivante, où y est une fonction de la variable indépendante t.
y "= - 1 / y² avec la condition initiale t = 0; y (0) = 0,5; y '(0) = 0
Trouvez la solution sur l'intervalle [0,5; 1.0] en utilisant un pas de 0,05.
Tracez le résultat: y vs t; y 'vs t
Les références
- Méthode d'Eurler Tirée de wikipedia.org
- Solveur Euler. Tiré de en.smath.com



Personne n'a encore commenté ce post.