
Méthode de Trachtenberg en quoi elle consiste, exemples
le Méthode Trachtenberg est un système permettant d'effectuer des opérations arithmétiques, principalement de multiplication, de manière simple et rapide, une fois ses règles connues et maîtrisées.
Il a été conçu par l'ingénieur d'origine russe Jakow Trachtenberg (1888-1953) alors qu'il était prisonnier des nazis dans un camp de concentration, comme une forme de distraction pour maintenir la raison tout en continuant en captivité..
Index des articles
- 1 De quoi il s'agit, avantages et inconvénients
- 2 exemples
- 2.1 - Multiplier un chiffre par 10 ou par 11
- 2.2 - Multiplication par les nombres de 12 à 19
- 2.3 - Extension des règles de multiplication par 13,… jusqu'à 19
- 3 Règles pour les produits par 6, 7 et 5
- 3.1 - Multiplication par 6
- 3.2 - Multiplication par 7
- 3.3 - Multiplication par 5
- 4 Règles pour les produits par 9
- 5 Multiplication par 8, 4, 3 et 2
- 5.1 - Multiplication par 8
- 5.2 - Multiplication par 4
- 5.3 - Multiplication par 3
- 5.4 - Multiplication par 2
- 6 Multiplier par des chiffres composites
- 6.1 Exercice
- 7 Références
De quoi il s'agit, avantages et inconvénients
L'avantage de cette méthode est que pour effectuer une multiplication, il n'est pas nécessaire de mémoriser les tables de multiplication, au moins en partie, il suffit de savoir compter et additionner, ainsi que de diviser un chiffre par deux.
L'inconvénient est qu'il n'y a pas de règle universelle pour multiplier par n'importe quel nombre, mais la règle varie en fonction du multiplicateur. Cependant, les motifs ne sont pas difficiles à mémoriser et permettent en principe d'effectuer des opérations sans l'aide de papier et de crayon..
Tout au long de cet article, nous nous concentrerons sur les règles pour se multiplier rapidement.
Exemples
Pour appliquer la méthode il faut connaître les règles, c'est pourquoi nous allons les présenter une par une et avec des exemples:
- Multipliez un nombre par 10 ou par 11
Règle de multiplication par 10
-Pour multiplier un nombre par 10, ajoutez simplement un zéro à droite. Par exemple: 52 x 10 = 520.
Règles de multiplication par 11
-Un zéro est ajouté au début et à la fin de la figure.
-Chaque chiffre est ajouté avec son voisin à droite et le résultat est placé sous le chiffre correspondant de la figure originale.
-Si le résultat dépasse neuf, alors l'unité est notée et un point est placé dessus pour rappeler que nous avons une unité qui sera ajoutée à la somme du chiffre suivant avec son voisin à droite.
Exemple détaillé de multiplication par 11
Multiplier 673179 par 11
06731790 x 11 =
--
= 7404969
Les étapes nécessaires pour arriver à ce résultat, illustrées par des couleurs, sont les suivantes:
-Le 1 de l'unité du multiplicateur (11) a été multiplié par le 9 du multiplicateur (06731790) et 0 a été ajouté. Le chiffre unitaire du résultat a été obtenu: 9.
-Ensuite, nous multiplions 1 par 7 et additionnons neuf à 16 et nous portons 1, nous plaçons les dix chiffres: 6.
-Après avoir multiplié 1 par 1, additionner le voisin de droite 7 plus 1 qu'il portait donne comme résultat 9 pour la centaine.
-Le chiffre suivant est obtenu en multipliant 1 par 3 plus le voisin 1, c'est 4 pour le chiffre des milliers.
-Multipliez 1 par 7 et ajoutez le voisin 3 résultant en 10, placez le zéro (0) comme dix mille chiffres et prend un.
-Puis 1 fois 6 plus le voisin 7 résultats 13 plus un 1 qui a eu des résultats 14, le 4 comme cent mille chiffres et prend 1.
-Enfin, 1 est multiplié par le zéro qui a été ajouté au début, ce qui donne zéro plus le voisin 6 plus un qui a été porté. Il s'avère finalement 7 pour le chiffre correspondant aux millions.
- Multiplication par les nombres de 12 à 19
Pour multiplier un nombre par 12:
-Un zéro est ajouté au début et un autre zéro à la fin du chiffre à multiplier.
-Chaque chiffre du chiffre à multiplier est doublé et ajouté avec son voisin de droite.
-Si la somme dépasse 10, une unité est ajoutée à l'opération de duplication suivante et additionnée avec le voisin.
Exemple de multiplication par 12
Multiplier 63247 par 12
0632470 x 12 =
-
758964
Les détails pour arriver à ce résultat, en suivant strictement les règles énoncées, sont indiqués dans la figure suivante:

- Extension des règles de multiplication par 13,… jusqu'à 19
La méthode de multiplication par 12 peut être étendue à la multiplication par 13, 14 à 19 simplement en changeant la règle du doublement par triplement pour le cas de treize, quadruplement pour le cas de 14 et ainsi de suite jusqu'à atteindre 19.
Règles pour les produits par 6, 7 et 5
- Multiplication par 6
-Ajoutez des zéros au début et à la fin de la figure pour multiplier par 6.
-Ajoutez la moitié de son voisin à droite à chaque chiffre, mais si le chiffre est impair, ajoutez 5 en plus.
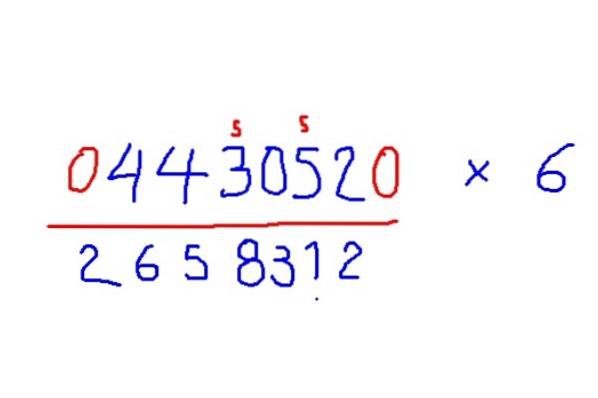
- Multiplication par 7
-Ajouter des zéros au début et à la fin du nombre à multiplier.
-Doublez chaque chiffre et ajoutez la moitié inférieure entière du voisin, mais si le chiffre est impair, ajoutez 5.
Exemple de multiplication par 7
-Multiplier 3412 par 7
-Le résultat est 23884. Pour appliquer les règles, il est recommandé de reconnaître d'abord les chiffres impairs et de placer un petit 5 au-dessus d'eux pour ne pas oublier d'ajouter ce chiffre au résultat..
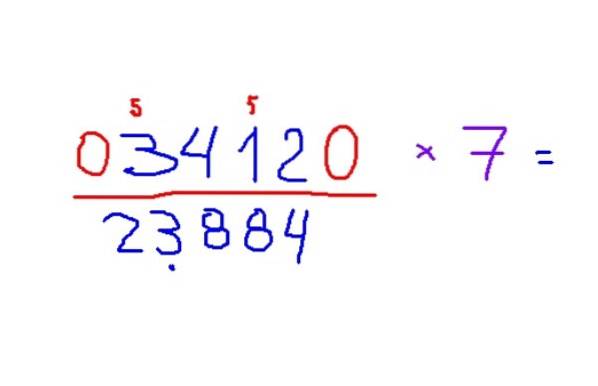
- Multiplication par 5
-Ajouter des zéros au début et à la fin du nombre à multiplier.
-Placez sous chaque chiffre la moitié inférieure entière du voisin à droite, mais si le chiffre est impair, ajoutez en plus 5.
Exemple multiplication par 5
Multiplier 256413 par 5
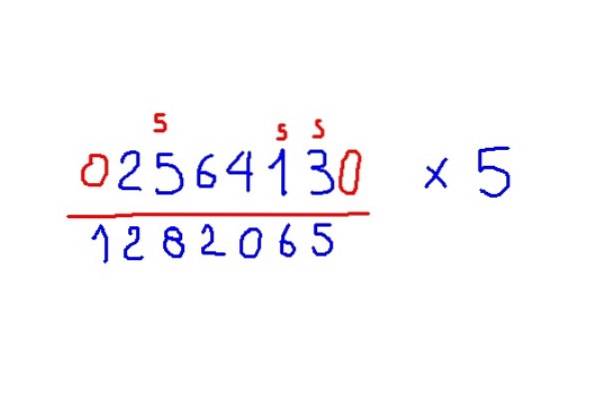
Règles pour les produits par 9
-Un zéro est ajouté au début et un autre à la fin du chiffre à multiplier par neuf.
-Le premier chiffre à droite est obtenu en soustrayant le chiffre correspondant du nombre à multiplier par 10.
-Ensuite, le chiffre suivant est soustrait de 9 et le voisin est ajouté.
-L'étape précédente est répétée jusqu'à ce que nous atteignions le zéro du multiplicande, où nous soustrayons 1 du voisin et le résultat est copié en dessous de zéro..
Exemple de multiplication par 9
Multipliez 8769 par 9:
087690 x 9 =
--
78921
Opérations
10 - 9 = 1
(9-6) + 9 = 1deux (les deux et prend 1)
(9-7) + 1 + 6 =9
(9-8) +7 =8
(8-1) = 7
Multiplication par 8, 4, 3 et 2
-Ajoutez des zéros au début et à la fin du nombre à multiplier.
-Pour le premier chiffre de la droite, soustrayez de 10 et le résultat est doublé.
-Pour les chiffres suivants soustraire de 9, le résultat est doublé et le voisin est ajouté.
-Lorsque vous atteignez zéro, soustrayez 2 au voisin de droite.
- Multiplication par 8
Exemple de multiplication par 8
-Multiplier 789 par 8
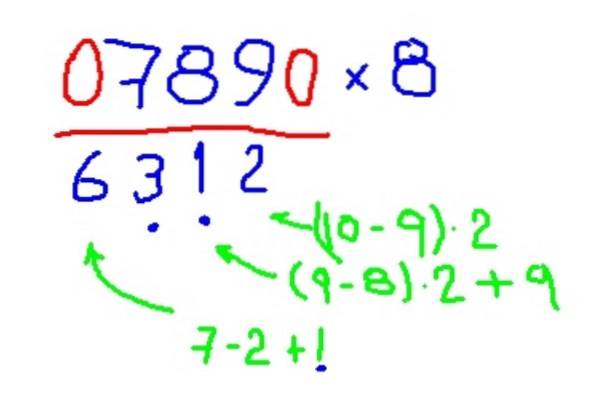
- Multiplication par 4
-Ajouter des zéros à droite et à gauche du multiplicande.
-Soustrayez le chiffre correspondant de l'unité de 10 en ajoutant 5 s'il s'agit d'un chiffre impair.
-Soustrayez chaque chiffre du multiplicande de 9 dans le formulaire, en ajoutant la moitié du voisin à droite et s'il s'agit d'un chiffre impair, ajoutez 5 en plus.
-Lorsque vous atteignez le zéro du début du multiplicande, placez la moitié du voisin moins un.
Exemple de multiplication par 4
Multiplier 365187 x 4
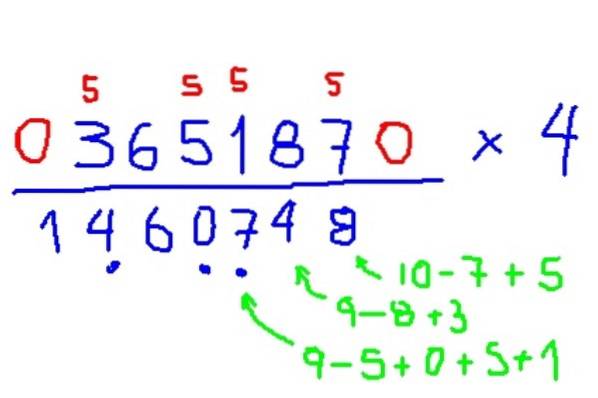
- Multiplication par 3
-Ajouter zéro à chaque extrémité du multiplicande.
-Soustrayez 10 moins le chiffre des unités et ajoutez 5 s'il s'agit d'un chiffre impair.
-Pour les autres chiffres, soustrayez 9, doublez le résultat, ajoutez la moitié du voisin et ajoutez 5 si c'est impair..
-Lorsque vous atteignez le zéro de l'en-tête, placez la moitié entière inférieure du voisin moins 2.
Exemple de multiplication par 3
Multiplier 2588 par 3

- Multiplication par 2
-Ajoutez des zéros aux extrémités et doublez chaque chiffre, s'il dépasse 10, ajoutez un au suivant.
Exemple multiplication par 2
Multiplier 2374 par 2
023740 x 2
04748
Multiplier par des chiffres composites
Les règles énumérées ci-dessus s'appliquent, mais les résultats sont exécutés vers la gauche par le nombre de places correspondant à des dizaines, des centaines, etc. Regardons l'exemple suivant:
Exercer
Multiplier 37654 par 498
0376540 x 498
301232 règle pour 8
338886 règle pour 9
150616 règle pour 4
18751692 somme finale
Les références
- Cutler, Ann. 1960 Le système de vitesse Trachtenberg des mathématiques de base. Doubleday & CO, NY.
- Dialnet. Système mathématique de base rapide. Récupéré de: dialnet.com
- Coin mathématique. Multiplication rapide par la méthode Trachtenberg. Récupéré de: rinconmatematico.com
- Le système de vitesse de Trachtenberg des mathématiques de base. Récupéré de: trachtenbergspeedmath.com
- Wikipédia. Méthode Trachtenberg. Récupéré de: wikipedia.com



Personne n'a encore commenté ce post.