
Biographie, contributions et inventions d'Archimède
Archimède de Syracuse (287 BC - 212 BC) était un mathématicien, physicien, inventeur, ingénieur et astronome grec de l'ancienne ville de Syracuse, sur l'île de Sicile. Ses contributions les plus marquantes sont le principe archimédien, le développement de la méthode d'épuisement, la méthode mécanique ou la création du premier planétarium..
Il est actuellement considéré comme l'une des trois figures les plus importantes des mathématiques anciennes avec Euclide et Apollonius, car leurs contributions ont signifié des avancées scientifiques importantes pour l'époque dans les domaines du calcul, de la physique, de la géométrie et de l'astronomie. À son tour, cela fait de lui l'un des scientifiques les plus éminents de l'histoire de l'humanité..

Malgré le fait que peu de détails de sa vie personnelle sont connus - et ceux qui sont connus sont d'une fiabilité douteuse -, ses contributions sont connues grâce à une série de lettres écrites sur son travail et ses réalisations qui ont été préservées jusqu'à aujourd'hui, appartenant à la correspondance qu'il entretenait pendant des années avec des amis et d'autres mathématiciens de l'époque.
Archimède était célèbre à son époque pour ses inventions, qui ont attiré beaucoup d'attention de ses contemporains, en partie parce qu'elles étaient utilisées comme dispositifs de guerre pour empêcher avec succès de nombreuses invasions romaines..
Cependant, il aurait prétendu que la seule chose vraiment importante était les mathématiques et que ses inventions n'étaient que le produit du passe-temps de la géométrie appliquée. Dans la postérité, ses travaux en mathématiques pures ont été beaucoup plus appréciés que ses inventions..
Index des articles
- 1 Biographie
- 1.1 Formation
- 1.2 Travaux scientifiques
- 1.3 Conflit à Syracuse
- 1.4 Décès
- 2 contributions scientifiques d'Archimède
- 2.1 Principe d'Archimède
- 2.2 Méthode mécanique
- 2.3 Explication de la loi du levier
- 2.4 Développement de la méthode d'épuisement ou de déplétion pour la démonstration scientifique
- 2.5 La mesure du cercle
- 2.6 La géométrie des sphères et des cylindres
- 3 inventions
- 3.1 Le compteur kilométrique
- 3.2 Le premier planétarium
- 3.3 La vis d'Archimède
- 3.4 La griffe d'Archimède
- 4 Références
Biographie
Archimède de Syracuse est né vers 287 av. On ne connaît pas beaucoup d'informations sur ses premières années, même si l'on peut dire qu'il est né à Syracuse, une ville considérée comme le principal port maritime de l'île de Sicile, aujourd'hui en Italie..
À cette époque, Syracuse était l'une des villes qui composaient la soi-disant Magna Grecia, qui était l'espace habité par des colons d'origine grecque vers la zone sud de la péninsule italienne et en Sicile..
Aucune information spécifique n'est connue sur la mère d'Archimède. En ce qui concerne le père, on sait que cela s'appelait Phidias et qu'il se consacrait à l'astronomie. Cette information sur son père est connue grâce à un fragment du livre Le comptoir de sable, écrit par Archimède, dans lequel il mentionne le nom de son père.
Héraclide, qui était un philosophe et astronome grec, était un ami proche d'Archimède et a même écrit une biographie à son sujet. Cependant, ce document n'a pas été conservé, donc toutes les informations qu'il contient sont inconnues..
D'autre part, l'historien, philosophe et biographe Plutarque a indiqué dans son livre intitulé Vies parallèles qu'Archimède avait une relation de sang avec Hiéron II, un tyran qui commandait à Syracuse depuis 265 av..
Formation
En raison du peu d'informations dont nous disposons sur Archimède, on ne sait pas avec certitude où il a obtenu sa première formation..
Cependant, divers historiographes ont déterminé qu'il y a une forte possibilité qu'Archimède ait étudié à Alexandrie, qui était le centre culturel et d'enseignement grec le plus important de la région..
Cette hypothèse est étayée par les informations fournies par l'historien grec Diodorus Siculus, qui a indiqué qu'Archimède a probablement étudié à Alexandrie.
En outre, dans beaucoup de ses travaux, Archimède lui-même fait mention d'autres scientifiques de l'époque dont les travaux étaient concentrés à Alexandrie, on peut donc supposer qu'il s'est réellement développé dans cette ville..
Certaines des personnalités avec lesquelles Archimède aurait interagi à Alexandrie sont le géographe, mathématicien et astronome Eratosthenes de Cyrène, et le mathématicien et astronome Conon de Sanos..
Motivation familiale
En revanche, le fait que le père d'Archimède soit astronome a peut-être eu une influence notable sur les inclinations qu'il a démontrées plus tard, car plus tard et dès son plus jeune âge, une attirance particulière pour le domaine des sciences.
Après son séjour à Alexandrie, on estime qu'Archimède est retourné à Syracuse.
Travail scientifique
Après son retour à Syracuse, Archimède a commencé à concevoir différents artefacts qui lui ont très vite fait gagner une certaine popularité parmi les habitants de cette ville. Dans cette période, il se consacre entièrement au travail scientifique, produit diverses inventions et déduit diverses notions mathématiques bien en avance sur son temps..
Par exemple, en étudiant les caractéristiques des figures solides courbes et planes, il en est venu à évoquer des concepts liés au calcul intégral et différentiel, qui a été développé plus tard..
De même, Archimède a été celui qui a défini que le volume associé à une sphère correspond à deux fois la taille du cylindre qui la contient, et c'est lui qui a inventé la poulie composée, sur la base de ses découvertes sur la loi du levier..
Conflit à Syracuse
Au cours de l'année 213 av.J.-C., des soldats romains entrèrent dans la ville de Syracuse et encerclèrent ses colons afin de les faire capituler..
Cette action a été menée par le militaire et homme politique grec Marco Claudio Marcelo dans le cadre de la deuxième guerre punique. Plus tard, elle était connue sous le nom d'épée de Rome, car elle a fini par conquérir Syracuse.
Au milieu du conflit, qui a duré deux ans, les habitants de Syracuse ont combattu les Romains avec courage et férocité, et Archimède a joué un rôle très important, car il s'est consacré à la création d'outils et d'instruments qui aideraient à vaincre les Romains..
Finalement, Marco Claudio Marcelo a pris la ville de Syracuse. Devant la grande intelligentsia d'Archimède, Marcelo a strictement ordonné de ne pas le blesser ni le tuer. Cependant, Archimède a été tué aux mains d'un soldat romain.
Décès
Archimède est mort en 212 avant JC. Plus de 130 ans après sa mort, en 137 av.J.-C., l'écrivain, homme politique et philosophe Marco Tulio Cicéron occupait un poste dans l'administration de Rome et voulait retrouver la tombe d'Archimède.
Cette tâche n'a pas été facile, car Cicéron n'a trouvé personne pour indiquer l'emplacement précis. Cependant, il l'a finalement eu, très proche de la porte d'Agrigente et dans un état déplorable.
Cicéron nettoya la tombe et découvrit qu'une sphère était inscrite à l'intérieur d'un cylindre, en référence à la découverte du volume qu'Archimède avait faite il y a quelque temps..
Versions sur sa mort
Première version
L'une des versions indique qu'Archimède était en train de résoudre un problème mathématique lorsqu'il a été approché par un soldat romain. On dit qu'Archimède lui aurait peut-être demandé un peu de temps pour résoudre le problème, alors le soldat l'aurait tué.
Deuxième version
La deuxième version est similaire à la première. Il raconte qu'Archimède résolvait un problème de mathématiques lorsque la ville a été prise.
Un soldat romain est entré dans sa concession et lui a ordonné d'aller rencontrer Marcelo, ce à quoi Archimède a répondu en disant qu'il devait d'abord résoudre le problème sur lequel il travaillait. Le soldat s'est fâché à la suite de cette réponse et l'a tué.
Troisième version
Cette hypothèse indique qu'Archimède avait entre les mains une grande diversité d'instruments mathématiques. Puis un soldat l'a vu et a pensé qu'il portait peut-être des objets de valeur, alors il l'a tué..
Quatrième version
Cette version illustre qu'Archimède était accroupi près du sol, contemplant certains plans qu'il étudiait. Apparemment, un soldat romain est venu par derrière et, ignorant qu'il s'agissait d'Archimède, l'a abattu.
Contributions scientifiques d'Archimède
Le principe d'Archimede
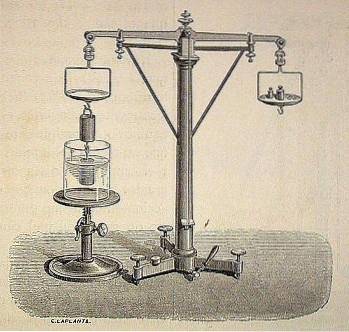
Le principe archimédien est considéré par la science moderne comme l'un des héritages les plus importants de l'époque antique.
Tout au long de l'histoire, et oralement, il a été transmis qu'Archimède est arrivé à sa découverte accidentellement grâce au roi Hiéron qui lui a demandé de vérifier si une couronne en or, commandée par lui, était faite uniquement d'or pur et ne contenait aucun autre métal. . Je devais faire ça sans détruire la couronne.
On dit que pendant qu'Archimède méditait sur la façon de résoudre ce problème, il a décidé de prendre un bain, et quand il est entré dans la baignoire, il s'est rendu compte que le niveau d'eau augmentait quand il s'y plongeait..
De cette manière, il en viendrait à découvrir le principe scientifique qui stipule que «tout corps totalement ou partiellement immergé dans un fluide (liquide ou gaz) reçoit une poussée ascendante, égale au poids du fluide délogé par l'objet»..
Ce principe signifie que les fluides exercent une force vers le haut - poussant vers le haut - sur tout objet submergé en eux, et que la quantité de cette force de poussée est égale au poids du liquide déplacé par le corps immergé, quel que soit son poids..
L'explication de ce principe décrit le phénomène de flottation, et se retrouve dans son Traité sur les corps flottants.
Le principe d'Archimède a été énormément appliqué dans la postérité pour la flottaison d'objets à usage de masse tels que les sous-marins, les navires, les gilets de sauvetage et les montgolfières..
Méthode mécanique
Une autre des contributions les plus importantes d'Archimède à la science était l'inclusion d'une méthode purement mécanique - c'est-à-dire technique - dans le raisonnement et l'argumentation des problèmes géométriques, ce qui signifiait une manière sans précédent de résoudre ce type de problème pour l'époque..
Dans le contexte d'Archimède, la géométrie était considérée comme une science exclusivement théorique, et le point commun était que les mathématiques pures descendaient vers d'autres sciences pratiques dans lesquelles ses principes pouvaient être appliqués..
Pour cette raison, il est aujourd'hui considéré comme le précurseur de la mécanique en tant que discipline scientifique..
Dans l'écriture où le mathématicien expose la nouvelle méthode à son ami Ératosthène, il indique qu'elle permet d'aborder des questions de mathématiques par la mécanique, et que d'une certaine manière il est plus facile de construire la preuve d'un théorème géométrique s'il est a déjà des connaissances pratiques préalables, que si vous n'en avez aucune idée.
Cette nouvelle méthode de recherche menée par Archimède deviendrait un précurseur de l'étape informelle de découverte et de formulation d'hypothèses de la méthode scientifique moderne..
Explication de la loi du levier
Bien que le levier soit une machine simple qui a été utilisée bien avant Archimède, c'est lui qui a formulé le principe qui explique son fonctionnement dans son traité Sur l'équilibre des plans.
En formulant cette loi, Archimède établit des principes qui décrivent les différents comportements d'un levier lors du placement de deux corps dessus, en fonction de leur poids et de leur distance par rapport au point d'appui..
De cette manière, il souligne que deux corps susceptibles d'être mesurés (proportionnels), situés sur un levier, s'équilibrent lorsqu'ils sont à des distances inversement proportionnelles à leur poids..
De la même manière, des corps incommensurables font (ce qui ne peut être mesuré), mais cette loi n'a été prouvée par Archimède qu'avec des corps du premier type..
Sa formulation du principe du levier est un bon exemple de l'application de la méthode mécanique, puisque comme il l'explique dans une lettre adressée à Dositeo, elle a été découverte dans un premier temps grâce à des méthodes mécaniques qu'il a mises en pratique..
Plus tard, il les a formulés en utilisant des méthodes de géométrie (théorique). Cette expérimentation sur les corps a également donné naissance à la notion de centre de gravité..
Développement de la méthode d'épuisement ou d'épuisement pour la démonstration scientifique
L'épuisement est une méthode utilisée en géométrie qui consiste à rapprocher des figures géométriques dont l'aire est connue, au moyen de l'inscription et de la circonscription, sur une autre dont l'aire est destinée à connaître.
Bien qu'Archimède n'ait pas été le créateur de cette méthode, il l'a développée de manière magistrale, réussissant à calculer à l'aide de celle-ci une valeur précise de Pi.
Archimède, selon la méthode de l'épuisement, inscrit et circonscrit des hexagones à une circonférence de diamètre 1, réduisant à une absurdité la différence entre l'aire des hexagones et celle de la circonférence..
Pour ce faire, il a coupé en deux les hexagones en créant des polygones avec jusqu'à 16 côtés, comme le montre la figure précédente..
De cette manière, il en est venu à préciser que la valeur de pi (de la relation entre la longueur d'une circonférence et son diamètre) est comprise entre les valeurs 3.14084507… et 3.14285714… .
Archimède a utilisé magistralement la méthode de l'épuisement car non seulement il a réussi à aborder le calcul de la valeur de Pi avec une marge d'erreur assez faible, et donc souhaitée, mais aussi, parce que Pi est un nombre irrationnel, à travers cette méthode et les résultats obtenus a jeté les bases qui germeraient dans le système de calcul infinitésimal, et plus tard, dans le calcul intégral moderne.
La mesure du cercle
Pour déterminer l'aire d'un cercle, Archimède a utilisé une méthode qui consistait à dessiner un carré qui s'inscrivait exactement à l'intérieur d'un cercle.
Sachant que l'aire du carré était la somme de ses côtés et que l'aire du cercle était plus grande, il commença à travailler sur l'obtention d'approximations. Il l'a fait en remplaçant le carré par un polygone à 6 côtés, puis en travaillant avec des polygones plus complexes..
Archimède a été le premier mathématicien de l'histoire à se rapprocher de faire un calcul sérieux du nombre Pi.
La géométrie des sphères et des cylindres
Parmi les neuf traités qui compilent les travaux d'Archimède en mathématiques et en physique, il y a deux volumes sur la géométrie des sphères et des cylindres.
Ce travail traite de la détermination que la surface de toute sphère de rayon est quatre fois celle de son plus grand cercle, et que le volume d'une sphère est des deux tiers de celui du cylindre dans lequel elle est inscrite..
Les inventions
Odomètre
Aussi connu sous le nom de compteur kilométrique, c'était une invention de ce célèbre homme.
Cet appareil a été construit sur le principe d'une roue qui, lorsqu'elle tourne, active des engrenages qui permettent de calculer la distance parcourue.
Selon ce même principe, Archimède a conçu différents types d'odomètres à des fins militaires et civiles..
Le premier planétarium
Sur la base du témoignage de nombreux écrivains classiques tels que Cicéron, Ovide, Claudien, Marciano Capela, Cassiodorus, Sextus Empiricus et Lactance, de nombreux scientifiques attribuent aujourd'hui la création du premier planétarium rudimentaire à Archimède..
C'est un mécanisme composé d'une série de "sphères" qui ont réussi à imiter le mouvement des planètes. Jusqu'à présent, les détails de ce mécanisme sont inconnus.
Selon Cicéron, les planétariums construits par Archimède étaient au nombre de deux. Dans l'un d'eux, la terre et les différentes constellations à proximité étaient représentées.
Dans l'autre, avec une seule rotation, le soleil, la lune et les planètes ont effectué leurs propres mouvements indépendants par rapport aux étoiles fixes de la même manière qu'ils le faisaient un jour réel. Dans ce dernier, en outre, des phases successives et des éclipses de lune ont pu être observées.
Vis d'Archimède
La vis d'Archimède est un dispositif utilisé pour transporter l'eau du bas vers le haut à travers une pente, au moyen d'un tube ou d'un cylindre.
Selon l'historien grec Diodore, grâce à cette invention l'irrigation des terres fertiles situées le long du Nil dans l'Égypte ancienne a été facilitée, car les outils traditionnels exigeaient un immense effort physique qui épuisait les ouvriers..
Le cylindre utilisé a à l'intérieur une vis de même longueur, qui maintient interconnecté un système d'hélices ou d'ailettes qui effectuent un mouvement rotatif entraîné manuellement par un levier rotatif.
De cette façon, les hélices parviennent à pousser n'importe quelle substance de bas en haut, formant une sorte de circuit infini.
Griffe d'Archimède
La griffe d'Archimède, ou la main de fer comme on l'appelle également, était l'une des armes de guerre les plus redoutables créées par ce mathématicien, devenant la plus importante pour la défense de la Sicile contre les invasions romaines..
Selon les recherches des professeurs de l'Université Drexel, Chris Rorres (Département de mathématiques) et Harry Harris (Département de génie civil et d'architecture), il s'agissait d'un gros levier auquel un grappin était attaché au levier.au moyen d'une chaîne qui y pendait.
Grâce au levier, le crochet a été manipulé de sorte qu'il tombe sur le navire ennemi, et l'objectif était de l'accrochage et de le soulever à un point tel qu'en le relâchant, il serait capable de le renverser complètement, ou de le faire s'écraser contre le rochers sur le rivage..
Rorres et Harris ont présenté au Symposium "Machines et structures extraordinaires de l'Antiquité" (2001), une représentation miniature de cet artefact intitulée "Une formidable machine de guerre: construction et fonctionnement de la main de fer d'Archimède"
Pour mener à bien ce travail, ils se sont appuyés sur les arguments des anciens historiens Polybe, Plutarque et Tito Livio..
Les références
- ASSIS, A. (2008). Archimède, le centre de gravité et la première loi de la mécanique [en ligne]. Récupéré le 10 juin 2017 sur bourabai.ru.
- DIJKSTERHUIS, E. (1956). Archimedes [en ligne]. Consulté le 9 juin 2015 sur le World Wide Web: books.google.co.ve/books.
- MOLINA, A. (2008). La méthode de recherche d'Archimède de Syracuse: intuition, mécanique et épuisement [en ligne]. Extrait le 10 juin 2017 du World Wide Webproduccioncientifica.luz.edu.
- O'CONNOR, J. et ROBERTSON, R. (1999). Archimedes of Syracuse [en ligne]. Récupéré le 9 juin 2017 de history.mcs.st-and.ac.uk.
- PARRA, E. (2009). Archimède: sa vie, ses œuvres et ses contributions aux mathématiques modernes [en ligne]. Récupéré le 9 juin 2017 sur lfunes.uniandes.edu.co.
- QUINN, L. (2005). Archimedes of Syracuse [en ligne]. Récupéré le 9 juin 2017 sur math.ucdenver.edu.
- RORRES, C. et HARRIS, H. (2001). Une formidable machine de guerre: construction et fonctionnement de la main de fer d'Archimède [en ligne]. Récupéré le 10 juin 2017 sur cs.drexel.edu.
- VITE, L. (2014). Principe d'Archimède [en ligne]. Consulté le 10 juin 2017 sur repository.uaeh.edu.mx.



Personne n'a encore commenté ce post.