
Les nombres quantiques à quoi servent-ils et à quoi servent-ils

Les nnombres quantiques sont utilisés pour décrire l'état quantique des électrons dans l'atome et proviennent de la solution de l'équation de Schrödinger pour le plus simple de tous: l'hydrogène.
L'équation de Schrödinger est une équation différentielle dont les solutions sont fonctions d'onde et sont désignés par la lettre grecque ψ. Des solutions infinies peuvent être proposées, et leur carré est égal à la probabilité de trouver l'électron dans une petite région de l'espace, appelée orbital.
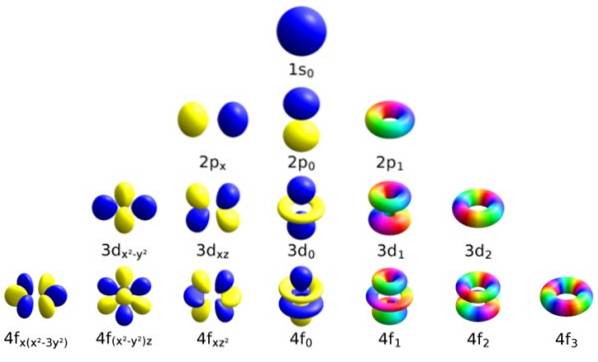
Chaque orbitale a des caractéristiques bien définies qui la distinguent des autres, comme l'énergie, le moment cinétique et le spin, propriété entièrement quantique de l'électron et responsable, entre autres, d'effets magnétiques..
La façon d'identifier chaque orbitale est de la distinguer par un ensemble de nombres qui la décrivent, et ce sont précisément les nombres quantiques:
-n: est le nombre quantique principal.
-ℓ: le nombre quantique azimutal.
-mℓ, est le nombre magnétique.
-ms, le numéro de rotation.
Index des articles
- 1 À quoi servent les nombres quantiques?
- 1.1 Fonctions Wave
- 2 Que sont les nombres quantiques?
- 2.1 Nombre quantique principal
- 2.2 Nombre quantique de moment azimutal ou angulaire
- 2.3 Nombre quantique magnétique mℓ
- 2.4 Nombre quantique de spin ms
- 3 Références
À quoi servent les nombres quantiques?
Les nombres quantiques sont utilisés pour décrire l'état des électrons à l'intérieur de l'atome. Ce modèle atomique dans lequel l'électron tourne autour du noyau est inexact, car il n'est pas compatible avec la stabilité atomique ou avec un grand nombre de phénomènes physiques observés.
C'est pourquoi le danois Niels Bohr (1885-1962) a fait une proposition audacieuse en 1913: l'électron ne peut être trouvé que dans certaines orbites stables, dont la taille dépend d'un entier appelé n.
Plus tard, en 1925, le physicien également autrichien Erwin Schrödinger (1887-1961) proposa une équation différentielle en dérivées partielles, dont les solutions décrivent l'atome d'hydrogène. Ce sont les fonctions d'onde ψ mentionnées au début.
Cette équation différentielle comprend les trois coordonnées spatiales plus le temps, mais lorsque cela n'est pas inclus, la solution de l'équation de Schrödinger est analogue à celle d'une onde stationnaire (une onde qui se propage entre certaines limites).
Fonctions Wave
L'équation de Schrödinger indépendante du temps est résolue en coordonnées sphériques et la solution est écrite comme le produit de trois fonctions, une pour chaque variable spatiale. Dans ce système de coordonnées, au lieu d'utiliser les coordonnées des axes cartésiens X, Oui Oui z les coordonnées sont utilisées r, θ Oui φ. De cette manière:
ψ (r, θ, φ) = R (r) ⋅f (θ) ⋅g (φ)
La fonction d'onde est intangible, mais la mécanique quantique nous dit que l'amplitude au carré:
| ψ (r, θ, φ) |deux
Autrement dit, le module ou la valeur absolue de la fonction d'onde, au carré, est un nombre réel qui représente la probabilité de trouver l'électron, dans une certaine région autour du point dont les coordonnées sont r, θ Oui φ.
Et ce fait est quelque chose de plus concret et tangible.
Pour trouver la fonction d'onde, vous devez résoudre trois équations différentielles ordinaires, une pour chaque variable r, θ Oui φ.
Les solutions de chaque équation, qui seront les fonctions R (r), f (θ) et g (φ), contiennent les trois premiers nombres quantiques mentionnés.
Que sont les nombres quantiques?
Nous décrivons brièvement la nature de chaque nombre quantique ci-dessous. Les trois premiers, comme indiqué précédemment, proviennent des solutions de l'équation de Schrödinger.
Le quatrième numéro a été ajouté par Paul Dirac (1902 - 1984) en 1928.
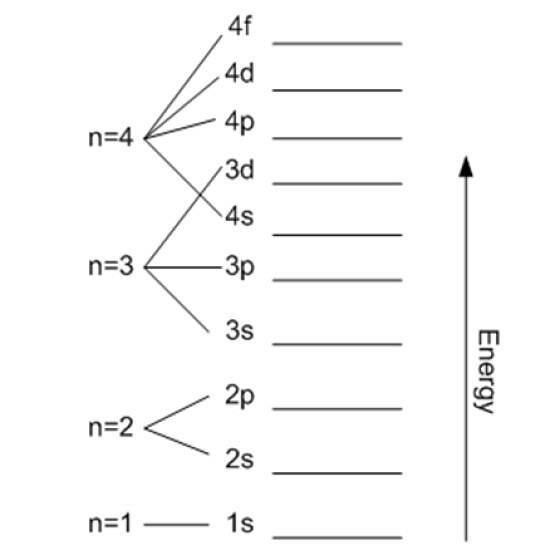
Nombre quantique principal
Il est désigné par n et indique la taille de l'orbitale autorisée, ainsi que l'énergie de l'électron. Plus sa valeur est élevée, plus l'électron est éloigné du noyau et son énergie sera également plus élevée, mais en retour cela réduit sa stabilité..
Ce nombre provient de la fonction R (r), qui est la probabilité de trouver l'électron à une certaine distance r du noyau, qui est déterminé par:
-Constante de Planck: h = 6,626 × 10 -3. 4 J.s
-Masse électronique met = 9,1 × 10-31 kg
-Charge électronique: e = 1,6 × 10-19 C.
-Constante électrostatique: k = 9 × 10 9 N.mdeux/ Cdeux
Lorsque n = 1 cela correspond au rayon de Bohr qui est d'environ 5,3 × 10−11 m.
À l'exception de la première couche, les autres sont subdivisées en sous-couches ou sous-niveaux. Chaque coque a une énergie en électron volt donnée par:

- K (n = 1)
- L (n = 2)
- M (n = 3)
- N (n = 4)
- O (n = 5)
- P (n = 6)
- Q (n = 7).
En théorie il n'y a pas de limite supérieure pour n, mais en pratique on observe qu'il n'atteint que n = 8. L'énergie la plus basse possible correspond à n = 1 et est celle du état fondamental.
Nombre quantique de moment azimutal ou angulaire
Désigné par la lettre italique ℓ, ce nombre détermine la forme des orbitales, en quantifiant la magnitude du moment cinétique orbital de l'électron.
Il peut prendre des valeurs positives et entières comprises entre 0 et n-1, par exemple:
-Lorsque n = 1, alors ℓ = 0 et il n'y a qu'un seul sous-niveau.
-Si n = 2, alors ℓ peut être égal à 0 ou 1, donc nous avons deux sous-niveaux.
-Et si n = 3, alors ℓ prend les valeurs 0, 1 et 2 et il y a 3 sous-niveaux.
Il peut être continué de cette manière indéfiniment, bien que comme dit précédemment, en pratique n monte à 8. Les sous-niveaux sont désignés par les lettres: s, p, ré, F Oui g et ils augmentent en énergie.

Nombre quantique magnétique mℓ
Ce nombre décide de l'orientation de l'orbitale dans l'espace et sa valeur dépend de celle de ℓ.
Pour un ℓ donné, il y a (2ℓ + 1) valeurs entières de m ℓ, qui correspondent aux orbitales respectives. Ceux-ci sont:
-ℓ, (- ℓ + 1),… 0,… (+ ℓ -1), + ℓ.
Exemple
Si n = 2, on sait que ℓ = 0 et ℓ = 1, alors m ℓ prend les valeurs suivantes:
-Pour ℓ = 0: m ℓ = 0.
-Pour ℓ = 1: m ℓ = -1, m ℓ = 0, m ℓ = +1
L'orbitale n = 2 a deux sous-niveaux, le premier avec n = 2, ℓ = 0 et m ℓ = 0. Ensuite, nous avons le deuxième sous-niveau: n = 2, ℓ = 1, avec 3 orbitales:
- n = 2, ℓ = 1, m ℓ = -1
- n = 2, ℓ = 1, m ℓ = 0
- n = 2, ℓ = 1, m ℓ = +1
Les trois orbitales ont la même énergie mais une orientation spatiale différente.
Nombre quantique de spin ms
Lors de la résolution de l'équation de Schrödinger en trois dimensions, les nombres déjà décrits apparaissent. Cependant, dans l'hydrogène, on observe une structure encore plus fine que ces nombres ne suffisent pas à expliquer.
Pour cette raison, en 1921, un autre physicien, Wolfgang Pauli, a proposé l'existence d'un quatrième nombre: le nombre de spin ms, qui prend des valeurs de + ½ ou -½.
Ce nombre décrit une propriété très importante de l'électron, qui est le tourner, mot qui vient de l'anglais tourner (pour tourner sur lui-même). Et le spin à son tour est lié aux propriétés magnétiques de l'atome.
Une façon de comprendre le spin est d'imaginer que l'électron se comporte comme un minuscule dipôle magnétique (un aimant avec des pôles nord et sud), grâce à une rotation autour de son propre axe. La rotation peut être dans le même sens que dans le sens horaire, ou dans le sens opposé.
Bien que Pauli ait suggéré l'existence de ce nombre, les résultats d'une expérience menée par Otto Stern et Walter Gerlach en 1922 l'avaient déjà anticipé..
Ces scientifiques ont réussi à diviser un faisceau d'atomes d'argent en deux en appliquant un champ magnétique non uniforme.
La valeur de ms ne dépend pas de n, ℓ et m ℓ. Sous forme graphique, il est représenté par une flèche: une flèche vers le haut indique un virage dans le sens des aiguilles d'une montre et une flèche vers le bas indique un virage dans le sens inverse des aiguilles d'une montre.
Principe d'exclusion de Pauli
Le comportement des électrons dans l'atome est résumé dans le principe d'exclusion de Pauli, qui stipule que deux électrons dans un atome ne peuvent pas exister dans le même état quantique.
Par conséquent, chaque électron doit avoir un ensemble différent de nombres quantiques n, ℓ, m ℓ et Ms.
L'importance des nombres quantiques et de ce principe réside dans la compréhension des propriétés des éléments du tableau périodique: les électrons sont organisés en couches selon n, puis en sous-couches selon ℓ et le reste des nombres.
Les références
- Alonso, M. 1971. Fondements quantiques et statistiques. Fonds interaméricain pour l'éducation.
- Bauer, W. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
- Chang, R. 2013. Chimie. 11ème. Édition. Éducation Mc Graw Hill.
- Eisberg-Resnick. 1989. Physique quantique. Limusa - Wiley.
- Giambattista, A. 2010. Physique. 2ème. Ed. McGraw Hill.
- Rex, A. 2011. Fondamentaux de la physique. Pearson.
- Tippens, P. 2011. Physique: concepts et applications. 7e édition. Mcgraw Hill.


Personne n'a encore commenté ce post.