
Concept de nombres négatifs, exemples, opérations

Les nombres négatifs sont ceux à gauche de la droite numérique, toujours précédés du signe -. Au moyen de négatifs, il est possible de représenter des quantités inférieures ou à gauche de 0.
Ces chiffres participent activement à la vie quotidienne: par exemple, si quelqu'un a une dette de 5 $, mais ne peut payer que 3 $, il doit 2 $. La dette est signalée par un signe négatif pour la distinguer du montant payé.
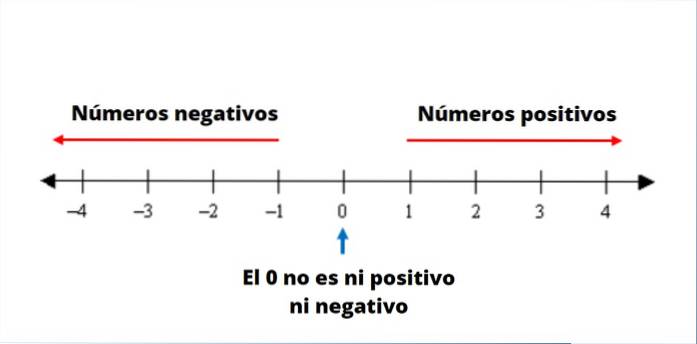
Les positions sous le niveau de la mer, les températures inférieures au point de congélation de l'eau et les sols sous le niveau de la rue peuvent être indiqués par des nombres négatifs..
Index des articles
- 1 À quoi servent les nombres négatifs?
- 2 Opérations avec des nombres négatifs
- 2.1 Valeur absolue
- 2.2 Signe
- 2.3 Somme
- 2.4 Soustraction
- 2.5 Multiplication
- 2.6 Division
- 2.7 Autonomisation
- 3 Références
À quoi servent les nombres négatifs?
L'existence de négatifs étend les opérations numériques possibles. Prenons l'exemple de la soustraction de deux nombres. Si ces nombres appartiennent au naturel 1, 2, 3, 4, 5 ... la soustraction n'a de sens que si elle est faite en soustrayant d'un autre nombre inférieur à lui.
Le résultat de l'opération 10 - 7 = 3 est raisonnable, car en principe on ne peut pas prendre plus d'une quantité qu'elle ne représente.
Cependant, les négatifs décriraient bien cette autre situation: nous voulons acheter quelque chose d'une valeur de 20 $, mais nous n'avons que 15 $ et nous empruntons 5 $ à un ami. La dette, comme nous l'avons dit, est marquée d'un signe négatif et donc 15 - 20 = -5, qui se lit comme "moins 5".
L'ensemble des entiers négatifs avec le naturel et 0, constitue le plus large ensemble d'entiers Z.
Mais les négatifs peuvent aussi être fractionnaires ou décimaux et appartenir à un ensemble encore plus grand: celui des nombres réels R, qui comprend le rationnel et l'irrationnel..
Avec tous, les opérations arithmétiques connues sont effectuées, en prenant soin d'opérer en suivant quelques règles simples de signes qui sont expliquées ci-dessous.
Opérations sur les nombres négatifs
Avant d'effectuer des opérations avec des nombres négatifs, vous devez établir quelques règles simples pour gérer le signe (-) qui doit toujours être ajouté au début et l'ordre des nombres.
Considérez la droite numérique montrée dans la figure, avec les négatifs à gauche de 0 et les positifs à droite.
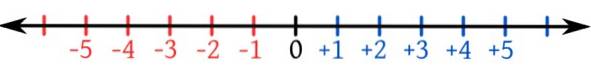
Les flèches sur la droite numérique dans les deux sens indiquent qu'il y a des nombres infinis. Notez également que l'ensemble numérique d'entiers est un ensemble ordonné et que tout nombre négatif est inférieur à 0 et tout nombre positif..
Ainsi, -4 est inférieur à 1 et -540 est inférieur à 84, par exemple.
Valeur absolue
La distance entre n'importe quel nombre et 0 est appelée valeur absolue. Cette distance est toujours positive et est indiquée par des barres verticales, comme ceci:
│-5│ = 5
│ + √6│ = √6
│-3 / 4│ = 3/4
│-10,2│ = 10,2
Autrement dit, la valeur absolue de tout nombre, qu'elle soit positive ou négative, est la valeur positive du nombre. Ce concept nous aidera plus tard lors de l'exploitation avec des nombres négatifs.
Signe
Un autre détail très important est la distinction entre le signe du nombre et le signe de l'opération..
Lorsqu'un nombre est positif, le signe du nombre est généralement omis et il est entendu qu'il est positif de toute façon, mais avec des négatifs ce qui n'est pas possible, il est donc nécessaire d'utiliser des parenthèses, voyons:
-Correct: 17 - (-6) ou aussi +17 - (-6)
-Incorrect: 17 - -6
-Incorrect: -5 + +7
-Correct: - 5 + (+7) ou aussi -5 + 7
Une fois que les concepts de valeur absolue, d'ordre et d'importance du signe négatif sont clairs, on peut passer aux opérations élémentaires.
Somme
On distingue les cas suivants, en commençant par la somme de deux positifs, dont la procédure est déjà très familière:
-Ajouter deux nombres positifs: (+ a) + (+ b) = a + b
Ce qui signifie que nous ajoutons comme d'habitude, voyons:
(+8) + (+5) = 8 + 5 = 13
-Ajouter deux nombres négatifs: (-a) + (-b) = - (a + b)
Dans ce cas, nous ajoutons les valeurs absolues des nombres et le résultat est précédé d'un signe négatif, comme ceci:
(-7) + (-11) = - (7+ 11) = - 18
-Ajouter un négatif et un positif: (+ a) + (-b)
Pour cette opération, les valeurs absolues sont soustraites et le résultat porte le signe du nombre avec la valeur absolue la plus élevée. Faisons quelques cas:
a) (-16) + (+3)
Les valeurs absolues respectives sont 16 et 3, le nombre avec la valeur absolue la plus élevée est 16, dont le signe est négatif, alors:
(-16) + (+3) = - (16 - 3) = -13
b) (+8) + (-3) = + (8-3) = +5 = 5
La somme des négatifs est également commutative, ce qui signifie que l'ordre des addends n'est pas important pour le résultat..
Les règles précédentes s'appliquent si vous souhaitez ajouter plus de deux nombres, ce qui peut être fait avec la propriété associative: a + b + c = (a + b) + c = a + (b + c).
Avant de regarder un exemple dans ce cas, regardons d'abord la soustraction de deux nombres entiers.
Soustraction
La soustraction est définie comme la somme du contraire. Le contraire d'un nombre a est -a, comme ceci:
-4 est l'opposé de + 4
½ est l'opposé de -½
Si on nous demande d'effectuer la soustraction de deux nombres, quel que soit le signe, on ajoute simplement l'opposé du second au premier:
a) (-53) - (+8) = (-53) + (-8) = - (53 + 8) = -61
b) (+7) - (-12) = (+7) + (+12) = 7 + 12 = 19
c) (+2) - (+ π) = (+2) + (-π) = 2 - π
Exemple
Effectuez l'opération suivante (+4) + (-7) + (+19)
Nous le réécrivons ainsi à l'aide de crochets pour indiquer l'opération à effectuer en premier:
(+4) + (-7) + (+19) = [(+4) + (-7)] + (+19) = [- (4 -7)] + 19 = [- (-3)] + 19 = 19 - (-3) = 19 + (+3) = 22
Multiplication
La règle des signes de multiplication est résumée dans la figure suivante:
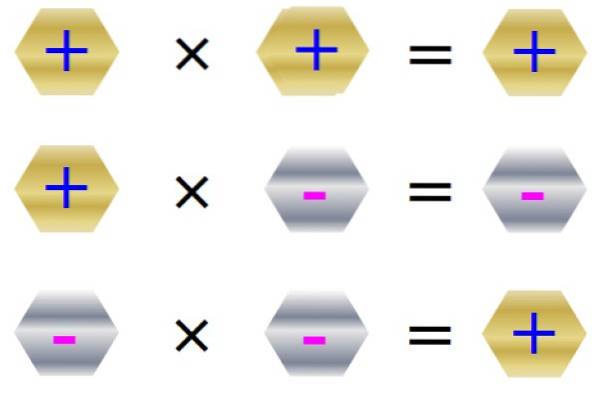
Propriétés de multiplication
-Commutativité: l'ordre des facteurs n'altère pas le produit, donc ≠ = b.a où a et b sont des nombres négatifs, entiers ou fractionnaires.
-Associativité: Soit a, b et c des entiers, il est vrai que (a.b). c = a. (avant JC)
-Distributivité par rapport à la somme: soit a, b et c des entiers, il est valide que a. (b + c) = a.b + a.c
Exemple
(-3/2) x [(-5) + (+4) - (+2)] = (-3/2) x (-5) + (-3/2) x (+4) + (- 3/2) x (-2) = (15 - 12 + 6) / 2 = 9/2
Vous pourriez également avoir résolu l'opération entre parenthèses en premier et multiplier le résultat par (-3/2), comme ceci:
(-3/2) x [-5 + 4 - 2] = (-3/2) x (-3) = 9/2
Division
La règle des signes de division est illustrée dans la figure suivante:
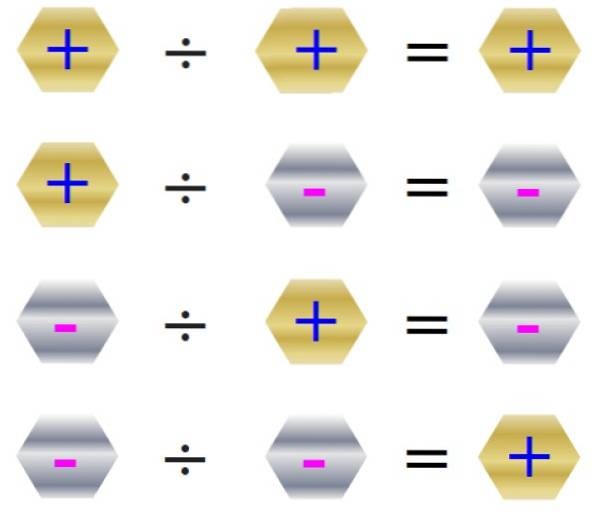
La division n'est pas commutative et généralement a ÷ b ≠ b ÷ a, la division par 0 n'est pas autorisée. Voyons un exemple:
(-54) ÷ (+3) = -18
Pour obtenir ce résultat, il suffit de faire le quotient et le signe est choisi selon le tableau présenté sur la figure, qui correspond à la troisième option de haut en bas.
Responsabilisation
L'autonomisation est l'opération de la forme unn, où a est la base et n l'exposant. La base et l'exposant peuvent avoir n'importe quel signe.
-Si la base est négative ou positive et que l'exposant est un entier pair, le résultat de l'opération est toujours positif.
-Lorsque la base est positive et que l'exposant est un entier impair, le résultat est positif.
-Et si la base est négative et l'exposant est un entier impair, le résultat est négatif.
Les exposants fractionnaires sont également exprimés sous forme de racine, par exemple une racine carrée équivaut à l'exposant fractionnaire ½, une racine cubique équivaut à l'exposant 1/3 et ainsi de suite.
Regardons quelques exemples:
a) (-3)3 = (-3) x (-3) x (-3) = -27
b) 16 -1/2 = 1 / √16 = ¼
c) (+8) 1/3 = racine cubique de 8 = 2
Les références
- Baldor, A. 1986. Arithmétique. Éditions et distributions du Codex.
- Figuera, J. 2000. Mathématiques 7e. Degré. Éditions CO-BO.
- Jiménez, R. 2008. Algèbre. Prentice Hall.
- Les mathématiques sont amusantes. Comment ajouter et soustraire des nombres positifs et négatifs. Récupéré de: mathisfun.com
- Wikipédia. Nombres négatifs. Récupéré de: es.wikipedia.org.



Personne n'a encore commenté ce post.