
Pente d'une formule de ligne et équations, représentation, exemples
La pente d'une ligne est la tangente de l'angle θ que forme ladite ligne avec l'axe horizontal, qui par convention est mesurée dans le sens antihoraire. La pente de toute ligne est toujours constante et c'est pourquoi c'est l'une de ses caractéristiques les plus essentielles..
Pour le calculer, vous devez connaître deux points sur la ligne, dont les coordonnées sont (x1,Oui1) et (xdeux,Ouideux). Un segment qui appartient à la ligne est dessiné entre les deux points, puis les segments qui représentent la distance entre x sont dessinés.1 et xdeux, et entre et1 et etdeux, comme dans la figure ci-dessous.
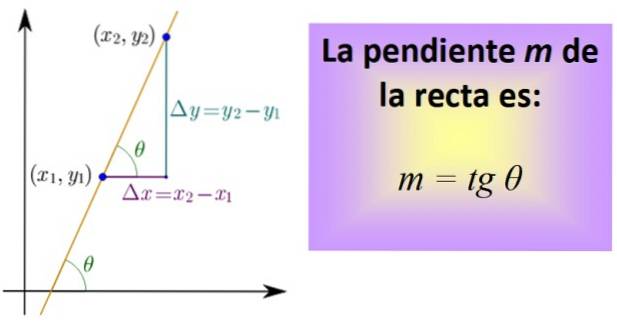
Les trois segments forment un triangle rectangle dont les jambes sont: Δx = xdeux - X1 y Δy = ydeux - Oui1. Ils correspondent respectivement à un déplacement horizontal et vertical..
Nous définissons maintenant un quotient, appelé tangente de l'angle θ et abrégé tg θ, qui est précisément la pente m de la ligne droite:
m = tg θ = Δy / Δx
Notez que pour une ligne, cet angle reste constant, quels que soient les points pris pour calculer sa tangente. Dans tous les cas, cette valeur nous donne une mesure de la pente de la ligne.
Grâce aux coordonnées des points sélectionnés, la formule de la pente est:
m = (y - y1 ) / (Xdeux - X1)
Index des articles
- 1 Représentation graphique
- 2 types de pente
- 3 Comment calculer la pente d'une ligne?
- 4 exercices résolus
- 4.1 - Exercice 1
- 4.2 - Exercice 2
- 5 exemples
- 5.1 Exemple 1
- 5.2 Exemple 2
- 6 Références
Représentation graphique
Ci-dessous, nous avons plusieurs situations dans lesquelles le concept de pente est pertinent. Sa valeur peut être facilement calculée en mesurant le déplacement vertical et horizontal respectif, puis en faisant le quotient indiqué au début.
Cela nous donne une idée de l'inégalité ou du déclin d'une structure, telle qu'une rampe, un toit ou une route:
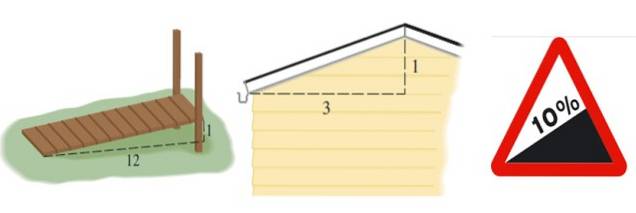
La pente de la rampe représentée sur la figure 2 à gauche est m = 1/12, celle du toit est m = 1/3 et celle de la route est exprimée en pourcentage. Un pourcentage de 10% signifie que pour chaque 100 mètres qui avancent horizontalement, 10 mètres de hauteur sont gagnés:
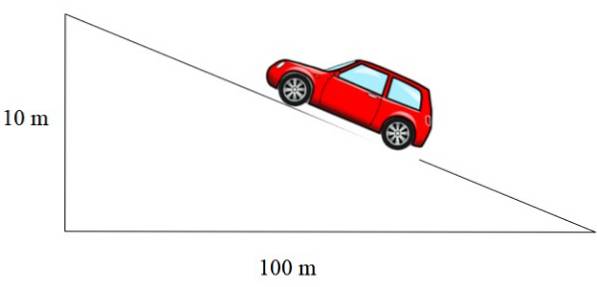
Dans ce cas, la pente est de 10/100 = 0,1, ce qui, exprimé en pourcentage, équivaut à 10%..
Types de pentes
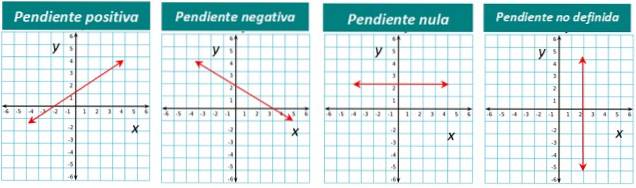
La pente d'une ligne peut être positive, négative ou nulle. Par exemple, la ligne représentée sur la figure 1 a une pente positive. On l'apprécie tout de suite car on voit que la ligne "monte" si on la voit de gauche à droite.
Si la ligne descend de gauche à droite, sa pente est négative. Et quand une ligne est horizontale, sa pente est nulle.
Enfin, pour les lignes verticales, la pente n'est pas définie.
La représentation graphique de chaque type est ci-dessous:
Comment calculer la pente d'une ligne?
Le calcul de la pente est très simple, il suffit de trouver le déplacement vertical et le déplacement horizontal, puis de faire le quotient entre les deux.
Lorsque nous avons le tracé de la ligne dans le plan cartésien, ces déplacements sont trouvés en choisissant deux points quelconques sur la ligne P1 Et Pdeux, déterminer ses coordonnées et appliquer la définition donnée au début:
m = (y - y1 ) / (Xdeux - X1 )
Puisque la valeur de la pente est indépendante du choix de P1 Et Pdeux , nous allons choisir un point P quelconque des coordonnées (x, y) qui appartient à la ligne, dont les coordonnées ne sont pas connues, et un autre point P1 dont les coordonnées sont: (x1,Oui1).
La pente est:
m = (y - y1) / (x - x1)
Nous pouvons effacer le Oui:
et et1 = m (x - x1)
Supposons maintenant que le point P1 est l'intersection de la ligne avec l'axe vertical, des coordonnées (0, b). En remplaçant ceci dans l'équation ci-dessus:
y - b = m (x - 0) → y = mx + b
Cette expression est connue sous le nom d'équation de la ligne sous la forme pente - interception, puisque la ligne est déterminée sans équivoque lorsque sa pente et son intersection avec l'axe vertical sont connues.
Connaître uniquement la pente ne suffit pas pour caractériser une ligne sur le plan, car des lignes infinies pourraient avoir la même pente, ce qui signifie qu'elles sont parallèles, mais passent par d'autres points.
Exercices résolus
- Exercice 1
Trouvez la pente de la ligne illustrée dans la figure suivante:
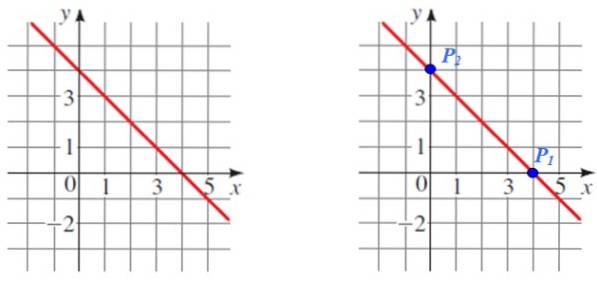
Solution
P1 Et Pdeux sont deux points faciles à lire qui seront utilisés pour le calcul, notez également que ce sont les intersections respectives avec les axes de coordonnées.
Les coordonnées de chaque point sont:
P1 (4.0) et Pdeux (0,4)
En substituant dans l'équation la pente:
m = (4 - 0) / (0 - 4) = 4 / (- 4) = -1
La pente est négative, ce qui était à prévoir après avoir regardé le graphique.
- Exercice 2
Trouvez l'équation de la droite passant par le point (1, -6) et parallèle à la droite y = 2x - 3.
Solution
La pente de la droite recherchée doit être la même que celle de y = 2x - 3, puisqu'elles sont parallèles. Pour cette droite la pente est m = 2, donc celle que nous recherchons a la forme:
et et1 = 2 (x - x1)
Maintenant, nous substituons le point par lequel passe notre ligne: x1 = 1 et y1 = -6.
y - (-6) = 2 (x - 1)
Donc y = 2x - 2-6 → y = 2x - 8
Exemples
Deux grandeurs peuvent être liées de telle sorte que leur graphique soit une ligne droite. Dans ce cas, on dit que les quantités ont une dépendance linéaire et la pente de la droite peut être interprétée comme le taux de changement d'une variable à l'autre.
Exemple 1
Supposons qu'une piscine soit remplie d'eau à un taux constante dans le temps. Naturellement, plus le temps passe, plus l'eau est stockée. Eh bien, la vitesse à laquelle la piscine est remplie est précisément la pente de la ligne qui relie le volume au temps:
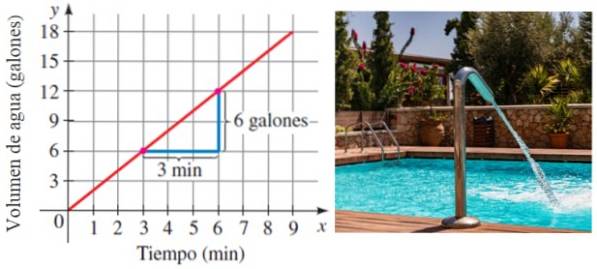
Dans cet exemple, la piscine se remplit au taux de 6/3 gallons par minute ou 2 gallons / minute.
Exemple 2
Lorsqu'un mobile se déplace en ligne droite à vitesse constante, la pente du graphe de position en fonction du temps n'est autre que ladite vitesse. Le graphique montre un mobile avec une vitesse positive, ce qui signifie qu'il s'éloigne de l'origine.
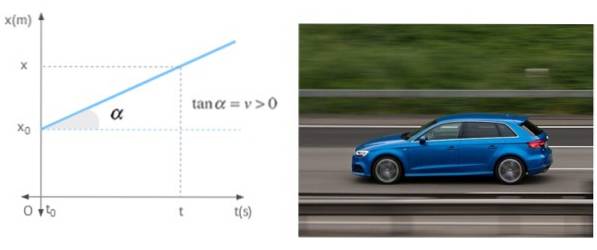
Les références
- Alvarez, J. La pente d'une autoroute. Récupéré de: geogebra.es.
- Carena, M. 2019. Manuel de mathématiques pré-universitaires. Université nationale du littoral.
- Hoffman, J. Sélection de sujets de mathématiques. Volume 4.
- Jiménez, R. 2008. Algèbre. Prentice Hall.
- Stewart, J. 2006. Précalcul: Mathématiques pour le calcul. 5ème. Édition. Apprentissage Cengage.
- Zill, D. 1984. Algèbre et trigonométrie. Mcgraw Hill.


Personne n'a encore commenté ce post.