
Formule de pression hydrostatique, calcul, exemples, exercices

La pression hydrostatique est celui qui exerce un fluide en équilibre statique en tout point de son intérieur, que ce soit une surface immergée dans celui-ci, les parois du récipient ou une portion de fluide faisant partie de la masse totale.
La façon dont les fluides exercent une pression diffère de celle des solides. Ceux-ci exercent une pression vers le bas, mais un liquide ou un gaz le fait dans toutes les directions.

Lorsqu'il s'agit d'un liquide, la pression augmente avec la profondeur, comme on le sait par expérience lors d'une immersion dans l'eau dans laquelle l'augmentation de la pression se fait sentir dans les oreilles. Cette pression provient du poids du fluide et du mouvement incessant des particules qui le composent, qui frappent en permanence la surface du corps immergé dans le fluide..
Si l'on suppose un liquide incompressible - ce qui est vrai dans la grande majorité des applications - sa densité reste constante et dans ce cas, la pression dépend linéairement de la profondeur..
Index des articles
- 1 formule
- 2 Exemples de pression hydrostatique
- 2.1 Structures où la pression hydrostatique est pertinente
- 3 exercices
- 3.1 - Exercice 1
- 3.2 - Exercice 2
- 4 Références
Formule
La pression hydrostatique est calculée à l'aide de l'expression suivante:
P = Pau m + ρ · g · h
Où:
-P la pression exercée en un point
-Pau m est la pression de l'atmosphère à la surface libre
-ρ est la densité du fluide
-g est l'accélération de la gravité
-h est la profondeur à laquelle vous souhaitez calculer la pression hydrostatique
La formule comprend les effets de l'atmosphère, mais de nombreux manomètres ou manomètres placent 0 à la pression atmosphérique, pour cette raison ce qu'ils mesurent est la pression différentielle ou pression relative, également appelée pression manométrique:
Pm = ρ · g · h
Quant aux gaz, ils se compriment ou se dilatent très facilement. Par conséquent, sa densité, qui est le rapport entre la masse et le volume, est généralement fonction d'autres paramètres, tels que l'altitude et la température, dans le cas des gaz atmosphériques..
La pression exercée par les gaz est souvent appelée pression aérostatique, le terme pression hydrostatique étant réservé aux liquides.
Exemples de pression hydrostatique
La pression hydrostatique ne dépend que de la profondeur, donc la forme ou la surface de la base du conteneur n'est pas pertinente.
Puisque la pression P est définie comme la composante perpendiculaire de la force F par unité de surface A:
P = F / A
Alors la force exercée par le liquide au fond d'un récipient peut être différente, mais comme elle est répartie sur des extensions différentes, la pression, qui est le rapport force / surface, est la même pour des points de même profondeur..
Considérez les conteneurs sur la figure. La pression est la même pour tous les points rouges qui sont au même niveau, bien qu'il y ait une plus grande quantité de fluide au-dessus de ce niveau dans le récipient central - plus large - qu'il n'y a le tube cylindrique et mince à l'extrême gauche..
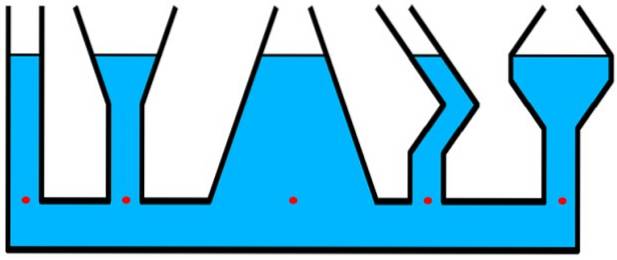
Structures où la pression hydrostatique est importante
-Les murs d'un barrage: bien que la force soit la même pour tous les points du fond plat, sur la paroi verticale elle grossit au fur et à mesure que la profondeur augmente, c'est pourquoi les murs de soutènement sont plus larges à la base qu'au sommet.
-Sur les murs et au fond d'une piscine.
-Dans les étoiles comme notre Soleil, où la pression hydrostatique équilibre la force de gravité et maintient l'étoile en marche. Lorsque cet équilibre est rompu, l'étoile s'effondre et subit des changements extrêmes dans sa structure..
-Réservoirs de stockage de liquides, conçus pour résister à la pression hydrostatique. Non seulement les murs, mais les portes qui facilitent le remplissage et l'extraction. Pour sa conception, il est pris en compte si le liquide est corrosif ainsi que la pression et la force qu'il exerce en fonction de sa densité.
-Pneus et ballons gonflés de manière à résister à la pression du fluide (gaz ou liquide) sans se déchirer.
-Tout corps immergé qui subit une poussée verticale vers le haut, ou «allégement» de son poids, grâce à la pression hydrostatique exercée par le liquide. Ceci est connu comme le Le principe d'Archimede.
Exercices
Le principe d'Archimède stipule que lorsqu'un corps est submergé, totalement ou partiellement, il subira une force verticale ascendante, appelée poussée. L'amplitude de la poussée est numériquement égale au poids du volume d'eau déplacé par l'objet..

Soit ρfluide la densité du fluide, Vs le volume immergé, g l'accélération de la pesanteur et B l'amplitude de la poussée, que nous pouvons calculer à l'aide de l'expression suivante:
B = ρfluide .Vs .g
- Exercice 1
Un bloc rectangulaire dont les dimensions sont de 2,0 cm x 2,0 cm x 6,0 cm flotte dans l'eau douce avec son plus long axe vertical. La longueur du bloc qui dépasse au-dessus de l'eau est de 2,0 cm. Calculer la densité du bloc.
Solution
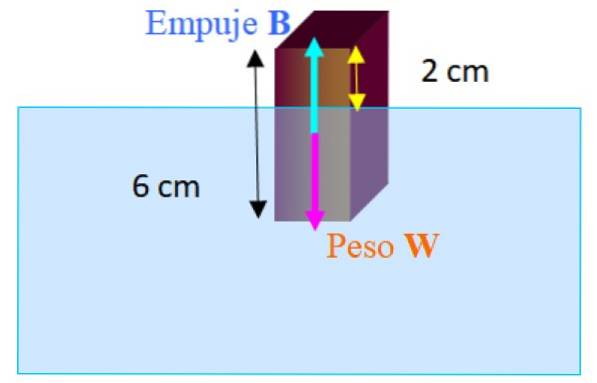
Les forces agissant sur le bloc sont le poids W vers le bas et la poussée B en haut. Au fur et à mesure que le bloc flotte en équilibre, nous avons:
∑ FOui = B - W = 0
B = W
L'amplitude du poids W est le produit de la masse m du bloc et de l'accélération de la pesanteur. Nous utiliserons la définition de la densité ρou alors comme quotient entre la masse m et le volume V du bloc:
ρou alors = m / V → m = ρou alors . V
De son côté, la poussée est:
B = ρfluide .Vs .g
Équivalence de la poussée et de la valeur du poids:
ρfluide .Vs .g = ρou alors . V.g
La gravité est annulée en étant un facteur des deux côtés et la densité du bloc peut être résolue comme suit:
ρou alors = ρfluide . (Vs / V)
La densité de l'eau en unités du système international est de 1000 kg / m3. Les volumes totaux V et immergés Vs, sont calculés en utilisant V = largeur x hauteur x profondeur:
V = 2,0 cm x 2,0 cm x 6,0 cm = 24,0 cm3
Vs = 2,0 cm x 2,0 cm x 4,0 cm = 16,0 cm3
Substituer des valeurs:
ρou alors = ρfluide . (Vs / V) = 1000 kg / m3 . (16/24) = 667 kg / m3
- Exercice 2
Calculer le pourcentage de volume immergé d'un morceau de glace flottant dans l'eau de mer à 0 ºC.
Solution
La glace flotte sur l'eau, car sa densité est inférieure: 916,8 Kg / m3, ce qui signifie qu'il se dilate lorsqu'il est refroidi, contrairement à la plupart des substances, qui augmentent de volume lorsqu'il est chauffé.

C'est une circonstance très chanceuse pour la vie, car alors les masses d'eau ne gèlent qu'en surface, restant liquide dans la profondeur.
La densité de l'eau de mer est un peu plus élevée que celle de l'eau douce: 1027 Kg / m3. Nous allons calculer la fraction volumique Vs / V:
Vs / V = ρou alors / ρfluide = 916,8 kilogrammes / m3 / 1027 kilogrammes / m3 = 0,8927
Cela signifie qu'environ 89% de la glace reste submergée sous l'eau. Seulement 11% sont visibles flottant sur la mer.
Les références
- Giambattista, A. 2010. Physique. 2ème. Ed. McGraw Hill.
- Knight, R. 2017. Physique pour les scientifiques et l'ingénierie: une approche stratégique. Pearson.
- Cimbala, C. 2006. Mécanique des fluides, principes fondamentaux et applications. Mc. Colline de Graw.
- Hibbeler, R. 2015. Mécanique des fluides. 1er. Ed. Pearson.
- Mott, R. 2006. Mécanique des fluides. 4ème. Édition. Éducation Pearson.
- Streeter, V. 1999. Mécanique des fluides. Mcgraw Hill.



Personne n'a encore commenté ce post.