
Explication de la pression de jauge, formules, équations, exemples
La pression manométrique Pm est celle qui est mesurée par rapport à une pression de référence, qui dans la plupart des cas est choisie comme pression atmosphérique Pau m au niveau de la mer. C'est alors un pression relative, un autre terme par lequel il est également connu.
L'autre façon dont la pression est généralement mesurée est de la comparer avec le vide absolu, dont la pression est toujours nulle. Dans un tel cas, nous parlons de la pression absolue, que nous noterons Pà.
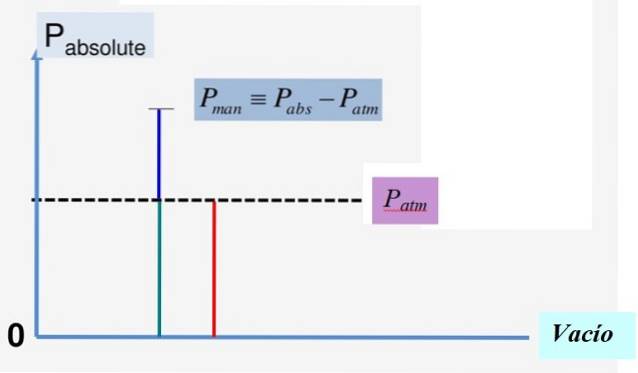
La relation mathématique entre ces trois grandeurs est:
Pà = Pau m + Pm
Donc:
Pm = Pà - Pau m
La figure 1 illustre bien cette relation. Puisque la pression de vide est 0, la pression absolue est toujours positive et il en va de même avec la pression atmosphérique Pau m.
La pression relative est souvent utilisée pour désigner des pressions supérieures à la pression atmosphérique, comme celle que l'on trouve dans les pneus ou celle au fond de la mer ou d'une piscine, qui s'exerce par le poids de la colonne d'eau. Dans ces cas, Pm > 0, puisque Pà > Pau m.
Cependant, il existe des pressions absolues inférieures à Pau m. Dans ces cas, Pm < 0 y recibe el nombre de Pression de vider et à ne pas confondre avec la pression du vide déjà décrit, qui est l'absence de particules capables d'exercer une pression.
Index des articles
- 1 Formules et équations
- 1.1 Variation de la pression avec la profondeur
- 2 exemples
- 2.1 Principe de Pascal
- 2.2 Paradoxe hydrostatique de Stevin
- 3 exercices
- 3.1 Exercice 1
- 3.2 Exercice 2
- 4 Références
Formules et équations
La pression dans un fluide - liquide ou gaz - est l'une des variables les plus significatives de son étude. Dans un fluide stationnaire, la pression est la même en tous points à la même profondeur quelle que soit l'orientation, tandis que le mouvement des fluides dans les tuyaux est provoqué par des changements de pression..
La pression moyenne est définie comme le quotient entre la force perpendiculaire à une surface F⊥ et l'aire de ladite surface A, qui s'exprime mathématiquement comme suit:
P = F⊥ /À
La pression est une quantité scalaire dont les dimensions sont la force par unité de surface. Les unités de sa mesure dans le Système international d'unités (SI) sont newton / mdeux, appelé Pascal et abrégé en Pa, en l'honneur de Blaise Pascal (1623-1662).
Multiples comme kilo (dix3) O méga (dix6) sont fréquemment utilisées, car la pression atmosphérique est généralement comprise entre 90 000 et 102 000 Pa, ce qui équivaut à: 90 à 102 kPa. Les pressions de l'ordre des mégapascals ne sont pas rares, il est donc important de se familiariser avec les préfixes.
En unités anglo-saxonnes, la pression est mesurée en livres / pieddeux, cependant, cela se fait généralement en livres / poucedeux ou alors psi (livres-force par pouce carré).
Variation de la pression avec la profondeur
Plus nous nous immergeons dans l'eau d'une piscine ou dans la mer, plus nous subissons de pression. Au contraire, à mesure que la hauteur augmente, la pression atmosphérique diminue.
La pression atmosphérique moyenne au niveau de la mer est établie à 101300 Pa ou 101,3 kPa, tandis que dans la fosse des Mariannes dans le Pacifique occidental - la profondeur la plus profonde connue - elle est environ 1000 fois supérieure et au sommet de l'Everest, elle n'est que de 34 kPa..
Il est clair que la pression et la profondeur (ou hauteur) sont liées. Pour le savoir dans le cas d'un fluide au repos (équilibre statique), on considère une portion de fluide en forme de disque, confinée dans un récipient, (voir figure 2). Le disque a une section transversale À, poids dW et hauteur mourir.
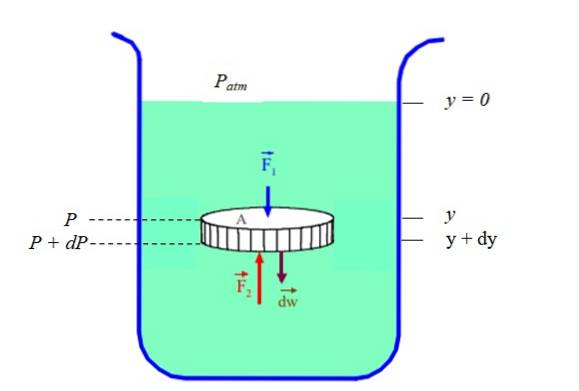
Nous appellerons P à la pression qui existe en profondeur "Oui"Y P + dP à la pression qui existe en profondeur (y + dy). Puisque la densité ρ du fluide est le rapport de sa masse dm et son volume dV, il faut que:
ρ = dm / dV ⇒ dm = ρ.dV
Par conséquent, le poids dW de l'élément est:
dW = g. dm = ρ.g.dV
Et maintenant, la deuxième loi de Newton s'applique:
Σ FOui = Fdeux - F1 - dW = 0
(P + dP) .A - P.A - ρ.g.dV = 0
(P + dP) .A - P.A - ρ.g. A. dy = 0
dP = ρ.g.dy
Solution de l'équation différentielle
Intégrer les deux côtés et considérer que la densité ρ, ainsi que la gravité g sont constantes, l'expression recherchée est trouvée:
Pdeux - P1 = ΔP = ρ.g. (etdeux - Oui1)
ΔP = ρ.g. ΔOui
Si dans l'expression précédente vous choisissez P1 comme pression atmosphérique et Oui1 comme surface du liquide, alors Ouideux il est situé à une profondeur h Oui ΔP = Pdeux - Pau m est la pression relative en fonction de la profondeur:
Pm = ρ.g.h
En cas de besoin de la valeur de pression absolue, ajoutez simplement la pression atmosphérique au résultat précédent.
Exemples
Pour mesurer la pression relative, un appareil appelé manomètre, qui offrent généralement des différences de pression. À la fin, le principe de fonctionnement d'un manomètre à tube en U sera décrit, mais regardons maintenant quelques exemples importants et les conséquences de l'équation précédemment déduite.
Principe de Pascal
L'équation ΔP = ρ.g. (etdeux - Oui1) peut être écrit comme P = Po + ρ.g.h, où P est la pression en profondeur h, tandis que Pou alors est la pression à la surface du fluide, généralement Pau m.
Evidemment à chaque fois qu'il augmente Po, augmente P dans la même quantité, tant qu'il s'agit d'un fluide dont la densité est constante. C'est précisément ce qui était supposé en considérant ρ constante et placez-la en dehors de l'intégrale résolue dans la section précédente.
Le principe de Pascal stipule que toute augmentation de la pression d'un fluide confiné en équilibre est transmise sans aucune variation à tous les points dudit fluide. Grâce à cette propriété, il est possible de multiplier la force F1 appliqué sur le petit piston à gauche, et obtenez Fdeux sur la droite.
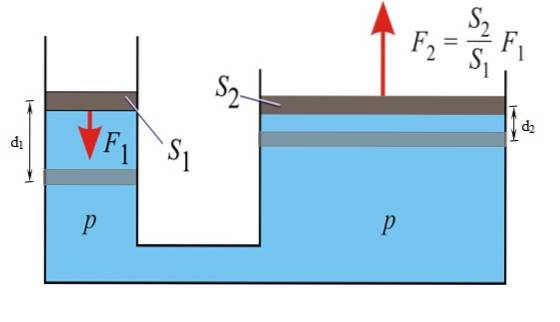
Les freins de voiture fonctionnent sur ce principe: une force relativement faible est appliquée sur la pédale, qui devient une force plus grande sur le cylindre de frein à chaque roue, grâce au fluide utilisé dans le système..
Paradoxe hydrostatique de Stevin
Le paradoxe hydrostatique stipule que la force due à la pression d'un fluide au fond d'un récipient peut être égale, supérieure ou inférieure au poids du fluide lui-même. Mais lorsque vous placez le conteneur sur le dessus de la balance, il enregistrera normalement le poids du fluide (plus celui du conteneur bien sûr). Comment expliquer ce paradoxe?
On part du fait que la pression au fond du récipient dépend exclusivement de la profondeur et est indépendante de la forme, comme cela a été déduit dans la section précédente.
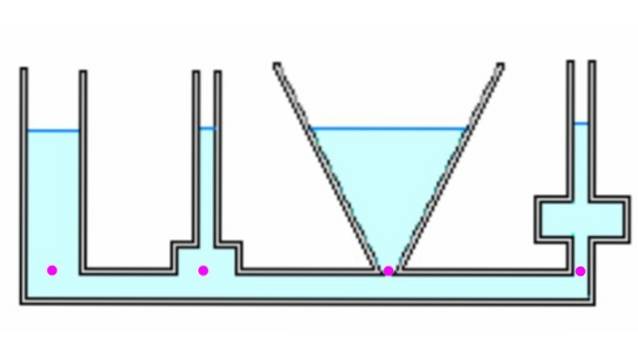
Regardons quelques conteneurs différents. Être communiqué, quand ils se remplissent de liquide, ils atteignent tous la même hauteur h. Les reflets sont à la même pression, puisqu'ils sont à la même profondeur. Cependant, la force due à la pression à chaque point peut différer du poids, (voir l'exemple 1 ci-dessous).
Exercices
Exercice 1
Comparez la force exercée par la pression sur le fond de chacun des récipients avec le poids du fluide et expliquez pourquoi les différences, le cas échéant.
Conteneur 1
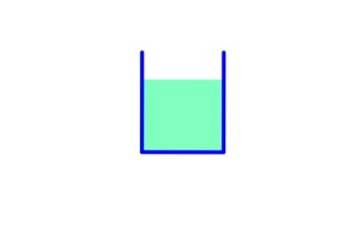
Dans ce conteneur, la surface de la base est A, donc:
Poids du fluide: mg = ρ.V.g = ρ . A .h. g
Pression sur le fond: ρ. g. h
Force due à la pression: F = P.A = ρ. g. h. À
Le poids et la force dus à la pression sont égaux.
Conteneur 2
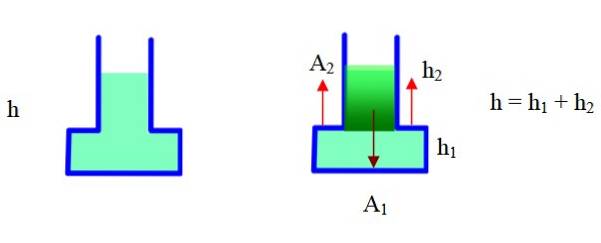
Le conteneur a une partie étroite et une partie large. Dans le diagramme de droite, il a été divisé en deux parties et la géométrie sera utilisée pour trouver le volume total. Zone Adeux c'est externe au conteneur, hdeux est la hauteur de la partie étroite, h1 est la hauteur de la partie large (base).
Le volume complet est le volume de la base + le volume de la partie étroite. Avec ces données, nous avons:
Poids fluide: m. g = ρ . g. V = ρ . g. [À1 .h1+ (À1 -Àdeux) .hdeux] =
= ρ . g (A1.Hadeuxhdeux) = ρ . g. À1.h - ρ . g. À.. hdeux (Il a été fait usage de h = h1 +hdeux)
Pression sur le fond: P = ρ. g. h
Force sur le fond due à la pression: F = P. A1 = ρ. g. h. À1
La comparaison du poids du fluide avec la force due à la pression montre que celle-ci est supérieure au poids.
Ce qui se passe, c'est que le fluide exerce également une force sur la partie de la marche dans le récipient (voir les flèches en rouge sur la figure) qui sont incluses dans le calcul ci-dessus. Cette force ascendante contrecarre celles exercées vers le bas et le poids enregistré par la balance en est le résultat. Selon cela, la grandeur du poids est:
W = Force sur le fond - Force sur la partie étagée = ρ . g. À1.h - ρ . g. À.. hdeux
Exercice 2
Un manomètre à tube ouvert est illustré sur la figure. Il se compose d'un tube en forme de U, dans lequel une extrémité est à la pression atmosphérique et l'autre est reliée à S, le système dont la pression doit être mesurée..
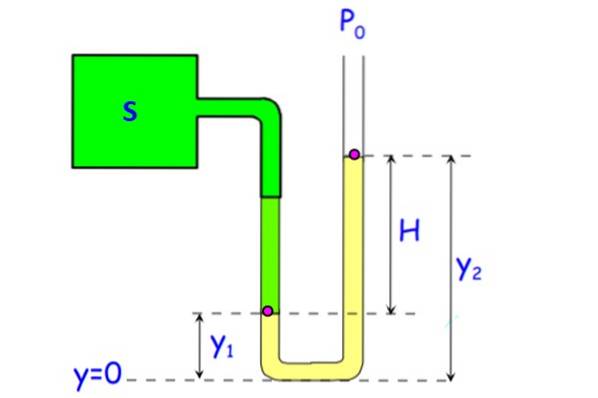
Le liquide dans le tube (représenté en jaune sur la figure) peut être de l'eau, bien que le mercure soit de préférence utilisé pour réduire la taille de l'appareil. (Une différence de 1 atmosphère ou 101,3 kPa nécessite une colonne d'eau de 10,3 mètres, rien de portable).
Il demande de trouver la pression relative Pm dans le système S, en fonction de la hauteur H de la colonne liquide.
Solution
La pression en bas pour les deux branches du tube est la même, car elles sont à la même profondeur. Soit PÀ la pression au point A, situé en y1 Et PB ceux du point B qui est à la hauteur etdeux. Puisque le point B est à l'interface du liquide et de l'air, la pression y est Pou alors. Dans cette branche du manomètre, la pression en bas est:
Po + ρ.g.ydeux
De son côté, la pression en bas pour la branche de gauche est:
P + ρ.g.y1
Où P est la pression absolue du système et ρ est la densité du fluide. Égaliser les deux pressions:
Po + ρ.g.ydeux = P + ρ.g.y1
Évacuer P:
P = Po + ρ.g.ydeux - ρ.g.y1 = Po + ρ.g (etdeux - Oui1) = Po + ρ.g. H
Par conséquent, la pression relative Pm est donné par P - Pou alors = ρ.g. H et pour avoir sa valeur, il suffit de mesurer la hauteur à laquelle le liquide manométrique monte et de le multiplier par la valeur de g et la densité du fluide.
Les références
- Cimbala, C. 2006. Mécanique des fluides, principes fondamentaux et applications. Mc. Graw Hill. 66-74.
- Figueroa, D. 2005. Série: Physique pour les sciences et l'ingénierie. Volume 4. Fluides et thermodynamique. Edité par Douglas Figueroa (USB). 3-25.
- Mott, R. 2006. Mécanique des fluides. 4ème. Édition. Pearson Education. 53-70.
- Shaugnessy, E. 2005. Introduction à la mécanique des fluides, Oxford University Press. 51 - 60.
- Stylianos, V. 2016. Une explication simple du paradoxe hydrostatique classique. Récupéré de: haimgaifman.files.wordpress.com


Personne n'a encore commenté ce post.