
Explication de la première condition d'équilibre, exemples, exercices
La première condition d'équilibre exige que la somme vectorielle de toutes les forces agissant sur un corps soit nulle, de sorte qu'il soit au repos (équilibre statique) ou avec un mouvement rectiligne uniforme (équilibre dynamique).
Cette somme de forces n'est autre que la force nette qui agit sur le corps, exprimée mathématiquement de cette manière:
Frapporter = 0
∑ F = 0

Dans l'espace, la première condition d'équilibre donne lieu à trois équations, une pour chaque dimension:
∑ FX = 0; ∑ FOui = 0 et ∑ Fz = 0
Lorsque ces équations sont satisfaites, l'objet ne se traduit pas ou si c'est le cas, ce sera à vitesse constante.
En regardant autour de nous, nous nous rendons compte que nous cherchons continuellement à satisfaire la première condition d'équilibre pour que les choses ne tombent pas.
Par conséquent, il cherche à compenser l'attraction gravitationnelle de la Terre au moyen de supports, cordes ou supports de certains, afin que de cette manière les choses restent en place et ne se retrouvent pas au sol..
D'autres fois, il faut empêcher les champs électromagnétiques externes d'interférer avec le fonctionnement des circuits électriques et des dispositifs de communication. Dans ce cas, ce sont les charges électriques qui doivent être en équilibre..
Index des articles
- 1 Exemples
- 1.1 Bâtiments
- 1.2 Feux de circulation et panneaux suspendus
- 1.3 Conducteurs en équilibre électrostatique
- 1.4 Plafonniers
- 1.5 Livres et objets sur les tables
- 1.6 Mesure de la viscosité d'un liquide
- 2 étapes pour appliquer la première condition d'équilibre
- 3 exercices résolus
- 3.1 - Exercice résolu 1
- 3.2 - Exercice résolu 2
- 4 Sujets d'intérêt
- 5 Références
Exemples
Un grand nombre d'objets du quotidien satisfont à la première condition d'équilibre, il s'agit d'observer attentivement:
Bâtiments
Les constructeurs recherchent la stabilité dans les constructions afin que les utilisateurs restent en sécurité. L'objectif de la statique est d'étudier les conditions d'un équilibre statique dans les bâtiments, les ponts, les routes et toutes sortes de structures..
Feux de circulation et panneaux suspendus
Ces dispositifs de signalisation doivent rester fixes pour remplir leurs fonctions, ils sont donc maintenus par des câbles, des poteaux et des tiges de manière à ce que la première condition d'équilibre soit remplie..

Conducteurs en équilibre électrostatiqueattique
Lorsque des matériaux conducteurs tels que le cuivre et d'autres métaux acquièrent une charge électrique, l'équilibre électrostatique est rapidement établi, laissant l'excès de charge sur la surface conductrice. À l'intérieur du champ électrique est nul.
Cet effet est souvent utilisé pour isoler les équipements électriques et électroniques des champs externes, en utilisant la cage dite de Faraday. La cage est en matériau conducteur et entoure l'équipement à protéger.
Pendant les tempêtes, les automobiles servent de cages de Faraday en protégeant les occupants des chocs électriques..
Plafonniers
Dans les systèmes d'éclairage, tels que les suspensions, la première condition d'équilibre est utilisée pour les fixer au plafond, au sol ou au mur.

Livres et objets sur des tables
Les objets placés sur des tables et des étagères remplissent la première condition d'équilibre. La force normale que le support exerce sur les objets est responsable de la compensation du poids.
Mesure de la viscosité d'un liquide
Pour déterminer la viscosité d'un liquide, un objet sphérique de diamètre connu tombe à l'intérieur et sa vitesse ralentira en raison de la résistance. La vitesse de la sphère est constante, étant ainsi en équilibre dynamique.
Plus la viscosité du liquide est élevée, plus la vitesse à laquelle la sphère se déplace à l'intérieur est faible.
Étapes pour appliquer la première condition d'équilibre
-Faites un diagramme du corps libre, montrant toutes les forces qui agissent sur le corps (omettez celles que le corps exerce sur les autres).
-Sélectionnez un système de coordonnées cartésien, en vous assurant que, dans la mesure du possible, les forces sont situées sur l'un des axes. La direction positive est généralement prise dans le sens du mouvement ou d'un mouvement possible.
-Déterminer les composantes cartésiennes de chaque force.
-L'application de la deuxième loi de Newton pour chaque composant, telle qu'établie au départ, reste donc un système d'équations.
-Résolvez le système d'équations soulevé à l'étape précédente.
Exercices résolus
- Exercice résolu 1
Le bloc de la figure, de la masse m, il se déplace vers le bas sur le plan incliné à l'angle θ à vitesse constante. Calculer la valeur du coefficient de frottement cinétique μk, si la masse du bloc est m = 5 kg et θ = 37º.

Solution
La première étape consiste à dessiner le diagramme du corps libre et à choisir un système de coordonnées cartésiennes pour exprimer chaque force de manière vectorielle. Les forces agissant sur le bloc sont:
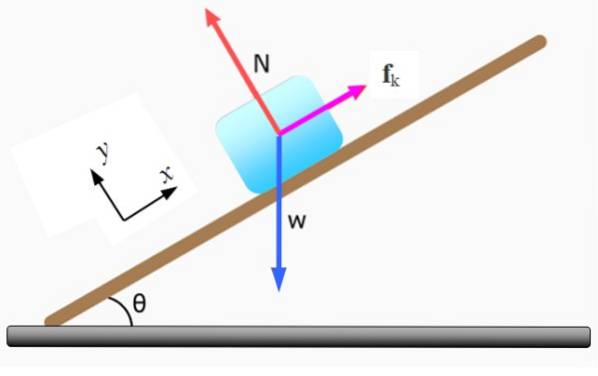
-Le normal N exercé par le plan incliné, est perpendiculaire à la surface de ce.
-Le poid W est dirigé verticalement vers le bas.
-Frottement cinétique Fk qui s'oppose au mouvement. S'il n'existait pas, le corps se déplacerait en descente avec une accélération égale à g.senθ.
Comme le poids W est incliné par rapport aux axes de coordonnées sélectionnés, il doit être décomposé en ses composantes cartésiennes:
WX = mg sin 37º = 5 kg x 9,8 m / sdeux x sin 37º = 29. 5 N
WOui = mg.cos 37º = 5 kg x 9,8 m / sdeux x cos 37º = 39,1 N
La deuxième loi de Newton est maintenant appliquée, mettant chaque somme à 0, car le bloc manque d'accélération lorsqu'il se déplace à vitesse constante:
∑ FOui = N - WOui = 0
∑ FX = WX - Fk = 0
L'amplitude du frottement cinétique est proportionnelle à la magnitude de la normale, le coefficient de frottement cinétique étant μk la constante de proportionnalité.
Fk = μk N
En même temps:
N = WOui = 39,1 N
Et aussi:
Fk = WX
Donc:
- 5 N = μk x 39,1 N
μk = 29,5 / 39,1 = 0,75
- Exercice résolu 2
Calculez l'amplitude des contraintes qui supportent le feu de signalisation d'une masse de 33 kg, illustrées sur la figure:
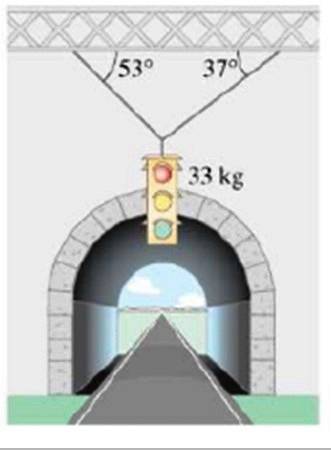
Solution
Le diagramme corps libre est fait à la fois pour le feu de signalisation et le nœud qui retient les câbles:
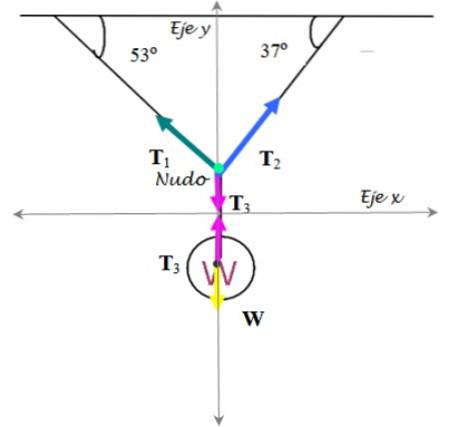
Feu de circulation
Sur elle acte: la tension T3 vers le haut et le poids W vers le bas. Donc:
∑ FOui = W - T3 = 0
Donc:
T3 = 33 kg x 9,8 m / sdeux = 323,4 N
Nouer
Les contraintes sont décomposées en leurs composantes cartésiennes:
∑ FOui = T1 sin 53º + Tdeux sen 37º - T3 = 0
∑ FX = Tdeux cos 37º - T1 cos 53º = 0
Et le système d'équations linéaires suivant est obtenu avec deux inconnues T1 et Tdeux :
- 0,6 T1 + 0,8 Tdeux = 0
0,8 T1 + 0,6 Tdeux = 323,4
La solution de ce système d'équations est: T1 = 258,7 N et Tdeux = 194,0 N
Thèmes d'intérêt
Conditions d'équilibre.
Deuxième condition d'équilibre.
Les références
- Bedford, 2000. A. Mécanique du génie: statique. Addison Wesley.
- Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 4. Systèmes de particules. Edité par Douglas Figueroa (USB).
- Giancoli, D. 2006. Physique: principes avec applications. 6e. Salle des Prentices Ed.
- Sears, Zemansky. 2016. Physique universitaire et physique moderne. 14e. Éd. Volume 1.
- Wikipédia. Statique (mécanique). Récupéré de: es.wikipedia.org.



Personne n'a encore commenté ce post.