le propriétés d'égalité font référence à la relation entre deux objets mathématiques, qu'il s'agisse de nombres ou de variables. Il est désigné par le symbole "=", qui se place toujours au milieu de ces deux objets. Cette expression est utilisée pour établir que deux objets mathématiques représentent le même objet; en un autre mot, que deux objets sont la même chose.
Il y a des cas où il est trivial d'utiliser l'égalité. Par exemple, il est clair que 2 = 2. Cependant, en ce qui concerne les variables, ce n'est plus trivial et a des utilisations spécifiques. Par exemple, si nous avons que y = x et d'autre part x = 7, nous pouvons conclure que y = 7 également.
L'exemple ci-dessus est basé sur l'une des propriétés de l'égalité, comme vous le verrez bientôt. Ces propriétés sont essentielles pour résoudre des équations (égalités impliquant des variables), qui constituent une partie très importante en mathématiques..
Index des articles
La propriété réflexive, dans le cas de l'égalité, indique que chaque nombre est égal à lui-même et est exprimé comme b = b pour tout nombre réel b.
Dans le cas particulier de l'égalité, cette propriété semble évidente, mais dans d'autres types de relations entre nombres, elle ne l'est pas. En d'autres termes, toutes les relations de nombres réels ne répondent pas à cette propriété. Par exemple, un tel cas de la relation «inférieur à» (<); ningún número es menor que sí mismo.
La propriété symétrique de l'égalité dit que si a = b, alors b = a. Peu importe l'ordre utilisé dans les variables, il sera conservé par la relation d'égalité.
Une certaine analogie de cette propriété avec la propriété commutative peut être observée dans le cas de l'addition. Par exemple, en raison de cette propriété, cela équivaut à écrire y = 4 ou 4 = y.
La propriété transitive sur l'égalité déclare que si a = b et b = c, alors a = c. Par exemple, 2 + 7 = 9 et 9 = 6 + 3; donc, par la propriété transitive, nous avons que 2 + 7 = 6 + 3.
Une application simple est la suivante: supposons que Julian a 14 ans et que Mario a le même âge que Rosa. Si Rosa a le même âge que Julian, quel âge a Mario?
Derrière ce scénario, la propriété transitive est utilisée deux fois. Mathématiquement, on l'interprète ainsi: soit «a» l'âge de Mario, «b» l'âge de Rosa et «c» l'âge de Julien. On sait que b = c et que c = 14.
Par la propriété transitive, nous avons que b = 14; c'est-à-dire que Rosa a 14 ans. Puisque a = b et b = 14, en utilisant à nouveau la propriété transitive, nous avons que a = 14; c'est-à-dire que l'âge de Mario est également de 14 ans.
La propriété uniforme est que si les deux côtés d'une égalité sont ajoutés ou multipliés par le même montant, l'égalité est préservée. Par exemple, si 2 = 2, alors 2 + 3 = 2 + 3, ce qui est clair, puisque 5 = 5. Cette propriété est très utile lorsque vous essayez de résoudre une équation.
Par exemple, supposons que l'on vous demande de résoudre l'équation x-2 = 1. Il est pratique de se rappeler que la résolution d'une équation consiste à déterminer explicitement la ou les variables impliquées, sur la base d'un nombre spécifique ou d'une variable préalablement spécifiée..
Pour en revenir à l'équation x-2 = 1, ce que vous devez faire est de trouver explicitement la valeur de x. Pour cela, la variable doit être effacée.
On a appris à tort que dans ce cas, puisque le nombre 2 est négatif, il passe de l'autre côté de l'égalité avec un signe positif. Mais ce n'est pas correct de le dire de cette façon.
Fondamentalement, vous appliquez la propriété uniforme, comme nous le verrons ci-dessous. L'idée est d'effacer "x"; c'est-à-dire, laissez-le seul d'un côté de l'équation. Par convention, il est généralement laissé sur le côté gauche.
A cet effet, le nombre à «éliminer» est -2. La façon de le faire serait d'ajouter 2, puisque -2 + 2 = 0 et x + 0 = 0. Pour pouvoir faire cela sans altérer l'égalité, la même opération doit être appliquée de l'autre côté.
Cela lui permet de réaliser la propriété uniforme: puisque x-2 = 1, si le nombre 2 est ajouté des deux côtés de l'égalité, la propriété uniforme dit qu'elle n'est pas altérée. Alors nous avons que x-2 + 2 = 1 + 2, ce qui équivaut à dire que x = 3. Avec cela, l'équation serait résolue.
De même, si vous voulez résoudre l'équation (1/5) y-1 = 9, vous pouvez continuer en utilisant la propriété uniforme comme suit:
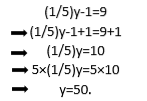
Plus généralement, les déclarations suivantes peuvent être faites:
- Si a-b = c-b, alors a = c.
- Si x-b = y, alors x = y + b.
- Si (1 / a) z = b, alors z = a ×
- Si (1 / c) a = (1 / c) b, alors a = b.
La propriété d'annulation est un cas particulier de la propriété uniforme, considérant en particulier le cas de la soustraction et de la division (qui, au fond, correspondent également à l'addition et à la multiplication). Cette propriété traite ce cas séparément.
Par exemple, si 7 + 2 = 9, alors 7 = 9-2. Ou si 2y = 6, alors y = 3 (en divisant par deux des deux côtés).
De manière analogue au cas précédent, grâce à la propriété d'annulation, les déclarations suivantes peuvent être établies:
- Si a + b = c + b, alors a = c.
- Si x + b = y, alors x = y-b.
- Si az = b, alors z = b / a.
- Si ca = cb, alors a = b.
Si nous connaissons la valeur d'un objet mathématique, la propriété de substitution indique que cette valeur peut être substituée dans n'importe quelle équation ou expression. Par exemple, si b = 5 et a = bx, alors en remplaçant la valeur de «b» dans la deuxième égalité, nous avons que a = 5x.
Un autre exemple est le suivant: si "m" divise "n" et aussi "n" divise "m", alors il doit avoir que m = n.
En effet, dire que "m" divise "n" (ou de manière équivalente, que "m" est un diviseur de "n") signifie que la division m ÷ n est exacte; c'est-à-dire que la division de "m" par "n" donne un nombre entier, pas une décimale. Cela peut être exprimé en disant qu'il existe un entier "k" tel que m = k × n.
Puisque "n" divise également "m", alors il existe un entier "p" tel que n = p × m. En raison de la propriété de substitution, nous avons que n = p × k × n, et pour cela, il y a deux possibilités: n = 0, auquel cas nous aurions l'identité 0 = 0; ou p × k = 1, d'où l'identité n = n.
Supposons que "n" soit différent de zéro. Alors nécessairement p × k = 1; par conséquent, p = 1 et k = 1. En utilisant à nouveau la propriété de substitution, en substituant k = 1 dans l'égalité m = k × n (ou de manière équivalente, p = 1 dans n = p × m), nous obtenons finalement que m = n, ce que nous voulions démontrer.
Tout comme précédemment on a vu que si une opération telle qu'une addition, une multiplication, une soustraction ou une division est faite dans les deux termes d'une égalité, elle est préservée, de la même manière que d'autres opérations qui n'altèrent pas une égalité peuvent être appliquées..
La clé est de toujours l'exécuter des deux côtés de l'égalité et de s'assurer au préalable que l'opération peut être effectuée. Tel est le cas de la responsabilisation; c'est-à-dire que si les deux côtés d'une équation sont élevés à la même puissance, nous avons toujours une égalité.
Par exemple, puisque 3 = 3, donc 3deux= 3deux (9 = 9). En général, étant donné un entier "n", si x = y, alors xn= etn.
Il s'agit d'un cas particulier d'autonomisation et est appliqué lorsque la puissance est un nombre rationnel non entier, tel que ½, qui représente la racine carrée. Cette propriété indique que si la même racine est appliquée aux deux côtés d'une égalité (dans la mesure du possible), l'égalité est préservée.
Contrairement au cas précédent, il faut faire attention ici à la parité de la racine à appliquer, car il est bien connu que la racine paire d'un nombre négatif n'est pas bien définie.
Dans le cas où le radical est pair, il n'y a pas de problème. Par exemple, si x3= -8, même s'il s'agit d'une égalité, vous ne pouvez pas appliquer une racine carrée aux deux côtés, par exemple. Cependant, si vous pouvez appliquer une racine cubique (ce qui est encore plus pratique si vous voulez connaître explicitement la valeur de x), obtenant ainsi que x = -2.
Personne n'a encore commenté ce post.