le rang, la distance ou l'amplitude, en statistique, est la différence (soustraction) entre la valeur maximale et la valeur minimale d'un ensemble de données provenant d'un échantillon ou d'une population. Si la plage est représentée par la lettre R et les données par X, la formule de la plage est simplement:
R = xmax - Xmin
Où xmax est la valeur maximale des données et xmin est le minimum.
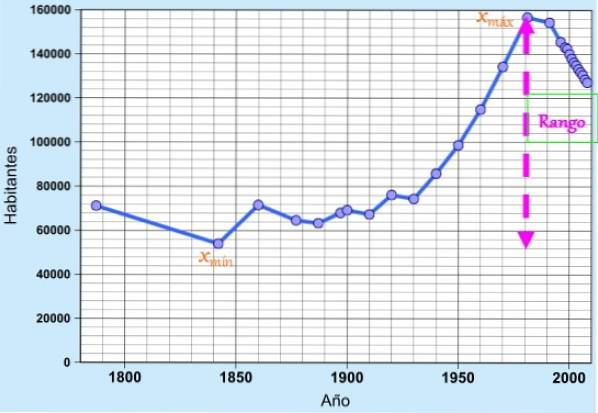
Le concept est très utile comme simple mesure de dispersion pour apprécier rapidement la variabilité des données, car il indique l'extension ou la longueur de l'intervalle où elles se trouvent..
Par exemple, supposons que la taille d'un groupe de 25 étudiants en génie de sexe masculin de première année dans une université soit mesurée. L'élève le plus grand du groupe mesure 1,93 m et le plus petit 1,67 m. Ce sont les valeurs extrêmes des exemples de données, leur chemin est donc:
R = 1,93 - 1,67 m = 0,26 m ou 26 cm.
La taille des élèves de ce groupe est répartie le long de cette plage.
Index des articles
La plage est, comme nous l'avons déjà dit, une mesure de la répartition des données. Une petite plage indique que les données sont plus ou moins proches et qu'il y a peu de dispersion. D'un autre côté, une plage plus large indique que les données sont plus dispersées..
Les avantages du calcul de la portée sont évidents: il est très simple et rapide à trouver, car il s'agit d'une simple différence.
Il a également les mêmes unités que les données avec lesquelles il fonctionne et le concept est très facile à interpréter pour tout observateur..
Dans l'exemple de la taille des élèves ingénieurs, si la portée avait été de 5 cm, on dirait que les élèves sont tous à peu près de la même taille. Mais avec une portée de 26 cm, nous supposons immédiatement qu'il y a des élèves de toutes les hauteurs intermédiaires dans l'échantillon. Cette hypothèse est-elle toujours correcte?
Si l'on regarde attentivement, il se peut que sur notre échantillon de 25 élèves ingénieurs, un seul d'entre eux mesure 1,93 et les 24 restants ont des hauteurs proches de 1,67 m..
Et pourtant la portée reste la même, bien que l'inverse soit parfaitement possible: que la hauteur de la majorité soit d'environ 1,90 m et qu'une seule mesure 1,67 m.
Dans les deux cas, la distribution des données est assez différente.
Les inconvénients de la distance comme mesure de dispersion sont parce qu'elle n'utilise que des valeurs extrêmes et ignore toutes les autres. Étant donné que la plupart des informations sont perdues, vous n'avez aucune idée de la façon dont les exemples de données sont distribués.
Une autre caractéristique importante est que la gamme de l'échantillon ne diminue jamais. Si nous ajoutons plus d'informations, c'est-à-dire que nous considérons plus de données, la plage augmente ou reste la même.
Et dans tous les cas, il n'est utile que lorsque vous travaillez avec de petits échantillons, sa seule utilisation comme mesure de dispersion dans de grands échantillons n'est pas recommandée..
Ce que vous devez faire est de compléter avec le calcul d'autres mesures de dispersion qui prennent en compte les informations fournies par les données totales: itinéraire interquartile, variance, écart type et coefficient de variation.
Nous nous sommes rendu compte que la faiblesse de la plage en tant que mesure de dispersion est qu'elle n'utilise que les valeurs extrêmes de la distribution des données, en omettant les autres..
Pour éviter cet inconvénient, le quartiles: trois valeurs appelées mesures de position.
Ils distribuent les données non groupées en quatre parties (d'autres mesures de position largement utilisées sont déciles et les centiles). Voici ses caractéristiques:
-Le premier quartile Q1 est la valeur des données telles que 25% d'entre elles sont inférieures à Q1.
-Le deuxième quartile Qdeux est le médian de la distribution, ce qui signifie que la moitié (50%) des données est inférieure à cette valeur.
-Enfin le troisième quartile Q3 souligne que 75% des données sont inférieures à Q3.
Ensuite, l'intervalle interquartile ou l'intervalle interquartile est défini comme la différence entre le troisième quartile Q3 et le premier quartile Q1 des données:
Intervalle interquartile = RQ = Q3 - Q1
De cette manière, la valeur de la plage RQ il n'est pas aussi affecté par les valeurs extrêmes. Pour cette raison, il est conseillé de l'utiliser lorsqu'il s'agit de distributions asymétriques, telles que celles des élèves très grands ou très petits décrites ci-dessus..
Il y a plusieurs façons de les calculer, ici nous en proposerons une, mais dans tous les cas il faut connaître les numéro de commande "Nou alors», Quelle est la place qu'occupe le quartile respectif dans la distribution.
Autrement dit, si, par exemple, le terme qui correspond à Q1 est le deuxième, troisième ou quatrième et ainsi de suite de la distribution.
Nou alors (Q1) = (N + 1) / 4
Nou alors (Qdeux) = (N + 1) / 2
Nou alors (Q3) = 3 (N + 1) / 4
Où N est le nombre de données.
La médiane est la valeur qui se trouve juste au milieu de la distribution. Si le nombre de données est impair, il n'y a aucun problème à le trouver, mais s'il est pair, alors les deux valeurs centrales sont moyennées pour devenir une.
Une fois le numéro de commande calculé, l'une de ces trois règles est respectée:
-S'il n'y a pas de décimales, les données indiquées dans la distribution sont recherchées et ce sera le quartile recherché.
-Lorsque le numéro d'ordre est à mi-chemin entre deux, les données indiquées par la partie entière sont moyennées avec les données suivantes, et le résultat est le quartile correspondant.
-Dans tous les autres cas, il est arrondi à l'entier le plus proche et ce sera la position du quartile.
Sur une échelle de 0 à 20, un groupe de 16 étudiants en mathématiques I ont obtenu les notes (points) suivantes à un examen de mi-session:
16, 10, 12, 8, 9, 15, 18, 20, 9, 11, 1, 13, 17, 9, 10, 14
Trouve:
a) La plage ou la plage des données.
b) Les valeurs des quartiles Q1 et alors3
c) L'intervalle interquartile.
La première chose à faire pour trouver le chemin est de classer les données par ordre croissant ou décroissant. Par exemple, dans l'ordre croissant, vous avez:
1, 8, 9, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20
En utilisant la formule donnée au début: R = xmax - Xmin
R = 20 - 1 points = 19 points.
Selon le résultat, ces qualifications ont une grande dispersion.
N = 16
Nou alors (Q1) = (N + 1) / 4 = (16 + 1) / 4 = 17/4 = 4,25
C'est un nombre avec décimales, dont la partie entière est 4. Ensuite, on passe à la distribution, on cherche les données qui occupent la quatrième place et sa valeur est moyennée avec celle de la cinquième position. Comme ils ont tous les deux 9 ans, la moyenne est également 9 et donc:
Q1 = 9
Maintenant, nous répétons la procédure pour trouver Q3:
Nou alors (Q3) = 3 (N + 1) / 4 = 3 (16 +1) / 4 = 12,75
Encore une fois, c'est un décimal, mais comme il n'est pas à mi-chemin, il est arrondi à 13. Le quartile que nous recherchons occupe la treizième position et est:
Q3 = 16
RQ = Q3 - Q1 = 16 - 9 = 7 points.
Ce qui, comme on le voit, est beaucoup plus petit que la plage de données calculée dans la section a), car le score minimum était de 1 point, une valeur bien plus éloignée du reste..
Personne n'a encore commenté ce post.