
Qu'est-ce que la réactance capacitive et comment la calculer?
La réactance capacitive est la résistance qu'un condensateur, élément régulateur du flux de charge dans un circuit de courant alternatif, oppose au passage du courant.
Dans un circuit constitué d'un condensateur et activé par une source de courant alternatif, la réactance capacitive X peut être définieC de la manière suivante:
XC = 1 / ωC

Ou aussi:
XC = 1 / 2πfC
Où C est la capacité du condensateur et ω est la fréquence angulaire de la source, liée à la fréquence f par:
ω = 2πf
La réactance capacitive dépend de l'inverse de la fréquence, donc aux hautes fréquences elle a tendance à être petite, tandis qu'aux basses fréquences, la réactance est grande.
L'unité du système international de mesure de la réactance capacitive est l'ohm (Ω), à condition que la capacité C du condensateur soit en farad, (abrégé F) et que la fréquence soit exprimée en secondes inverses (s-1).
Pendant que la charge dure, une tension et un courant alternatifs sont établis à travers le condensateur, dont les amplitudes ou valeurs maximales, notées respectivement VC et moiC, sont liés par la réactance capacitive de manière analogue à la loi d'Ohm:
VC = JeC ⋅ XC
Dans un condensateur, la tension est de 90 ° derrière le courant, ou le courant est de 90 ° en avance sur le courant, comme vous préférez. Dans tous les cas la fréquence est la même.
Quand XC est très grand, le courant a tendance à être petit et fait tendre la valeur de X à l'infiniC, le condensateur se comporte comme un circuit ouvert et le courant est nul.
Index des articles
- 1 Comment calculer la réactance capacitive
- 1.1 Courant et tension aux bornes du condensateur
- 2 Impédance complexe du condensateur
- 2.1 Impédance d'un circuit RC série
- 3 Applications de la réactance capacitive
- 4 Références
Comment calculer la réactance capacitive
Voyons un exemple de calcul de la réactance capacitive: supposons qu'un condensateur de 6 μF soit connecté à une prise de courant alternatif de 40 V et de fréquence F 60 Hz.
Pour trouver la réactance capacitive, la définition donnée au début est utilisée. La fréquence angulaire ω est donnée par:
ω = 2πf = 2π x 60 Hz = 377 s-1
Ensuite, ce résultat est remplacé dans la définition:
XC = 1 / ωC = 1 / (377 s-1x 6 x10 -6 F) = 442,1 ohms
Voyons maintenant l'amplitude du courant circulant dans le circuit. Puisque la source offre une tension d'amplitude VC = 40 V, nous utilisons la relation entre la réactance capacitive, le courant et la tension pour calculer l'amplitude du courant ou du courant maximal:
jeC = VC / XC = 40 V / 442,1 ohm = 0,09047 A = 90,5 m A.
Si la fréquence devient très grande, la réactance capacitive devient petite, mais si la fréquence devenait 0 et que nous avions un courant continu, la réactance aurait tendance à être infinie..
Courant et tension aux bornes du condensateur
Lorsqu'un condensateur est connecté à une source de courant alternatif, lorsqu'il oscille et change de polarité, le condensateur subit des charges et des décharges alternées..
Pour une fréquence de 60 Hz comme celle de l'exemple, la tension est positive 60 fois par seconde, et négative encore 60 fois par seconde.
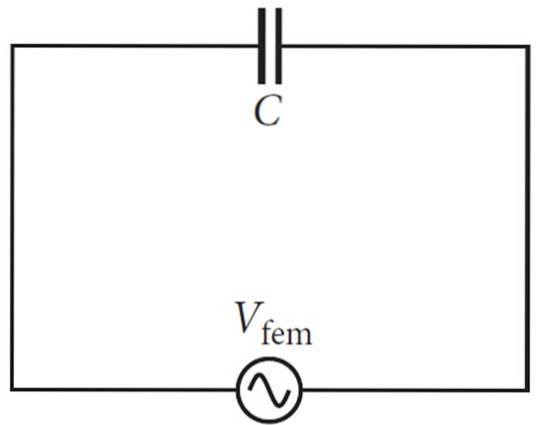
L'augmentation de la tension pousse le courant dans un sens, mais si le condensateur se décharge, le courant est produit dans la direction opposée à la première..
Oui VC (t) = Vm sin ωt, sachant que la capacité est le rapport entre la charge et la tension, nous aurons la charge:
C = q / V → q (t) = CV = CVm sen ωt
Et en ayant la charge en fonction du temps, nous aurons le courant, qui en est le dérivé:
jeC(t) = CVm ω cos ωt
Mais le sinus et le cosinus sont liés par: cos α = sin (α + π / 2), donc:
jeC(t) = CVm ω sin (ωt + π / 2) = IC sin (ωt + π / 2)
Avec moiC = CVC ω
Comme vous pouvez le voir, il y a une différence de 90º d'avance du courant par rapport à la tension, comme cela a été commenté au début.
Dans la description de ce type de circuits, le concept de phaseur, qui est très similaire à un vecteur et permet de représenter toute grandeur alternative telle que le courant, la tension ou l'impédance dans le plan complexe.
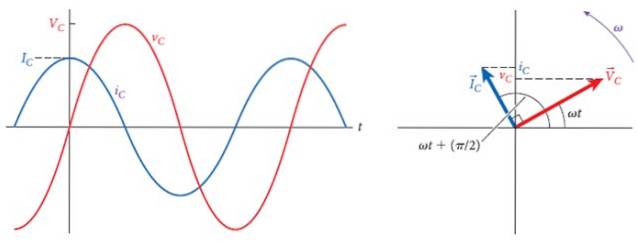
La figure suivante montre, à droite, les phaseurs de tension et de courant dans le condensateur, qui forment un angle de 90 ° entre eux, ce qui correspond à la différence de phase entre les deux..
Sur la gauche se trouvent les graphiques respectifs, d'amplitudes différentes, mais de même fréquence. Dans le temps, le courant dépasse la tension et lorsqu'il est maximum, le courant est nul et lorsque la tension est nulle, le courant est maximum mais avec la polarité inversée.
Impédance de condensateur complexe
Dans un circuit avec résistances, condensateurs et inductances, la réactance est la partie imaginaire de l'impédance Z, une grandeur complexe qui, dans les circuits à courant alternatif, a un rôle similaire à celui de la résistance électrique pour les circuits à courant continu..
En fait, l'impédance d'un circuit est définie comme le rapport de la tension au courant:
Z = V / I
Pour un condensateur ou un condensateur, son impédance est donnée par le quotient:
ZC = v (t) / i (t) = VC sin ωt / IC sin (ωt + π / 2)
Une façon d'exprimer la tension et le courant sous forme de phaseurs consiste à indiquer l'amplitude et l'angle de phase (forme polaire):
v (t) = VC ∠ 0º
i (t) = IC ∠ 90º
Donc:
ZC = VC ∠ 0º / IC ∠ 90º = (VC / JEC) ∠ 0º -90º =
= VC / CVC ω ∠ -90º = (1 / ωC) ∠ -90º =
ZC = (- j) XC
Autrement dit, l'impédance du condensateur est sa réactance capacitive multipliée par le négatif de l'unité imaginaire.
Impédance d'un circuit RC série
L'impédance d'un circuit de courant alternatif avec des résistances, des condensateurs et des inductances peut également être représentée de manière binomiale par:
Z = R + jX
Dans cette équation, R représente la résistance, qui correspond à la partie réelle, j est l'unité imaginaire et X est la réactance, qui peut être capacitive ou inductive ou une combinaison des deux, si ces éléments sont présents en même temps dans le circuit.
Si le circuit contient une résistance et un condensateur en série, leur impédance est:
Z = ZR + ZC
Comme en résistance la tension et le courant sont en phase, l'impédance résistive est simplement la valeur de la résistance R.
Dans le cas de l'impédance capacitive, nous avons déjà vu que ZC = -jXC , donc l'impédance du circuit RC est:
Z = R - jXC = R - j (1 / ωC)
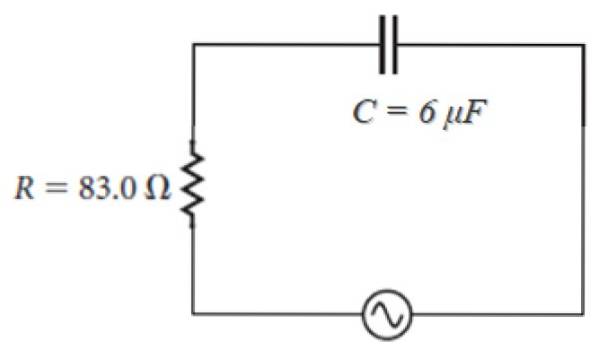
Par exemple dans le circuit illustré ci-dessous, dont la source est de la forme:
100 V ⋅ sin (120πt)
En observant que ω = 120π, l'impédance est:
Z = 83,0 - j [(1 / (120π ⋅ 6 x 10-6)] ohm = 83,0 - 442,1 j ohm.
Applications de réactance capacitive
Les filtres passe-haut, les filtres passe-bas, les circuits de type pont pour mesurer les capacités et les inductances, et les circuits de déphasage sont parmi les principales applications des circuits contenant des réactances capacitives, en combinaison avec des inductances et des résistances électriques..
Dans les chaînes stéréo, certains haut-parleurs sont équipés de haut-parleurs séparés. woofer (plus grand) pour les basses fréquences et tweeter ou petite corne pour les hautes fréquences. Cela améliore les performances et la qualité audio.
Ils utilisent des condensateurs qui empêchent l'arrivée de basses fréquences dans le tweeter, tandis que dans le woofer une inductance est ajoutée pour éviter les signaux haute fréquence, car l'inductance a une réactance proportionnelle à la fréquence: XL = 2πfL.
Les références
- Alexander, C. 2006. Principes de base des circuits électriques. 3e. Édition. Mc Graw Hill.
- Bauer, W. 2011. Physique pour l'ingénierie et les sciences. Volume 2. Mc Graw Hill.
- Figueroa, D. 2005. Série: Physique pour les sciences et l'ingénierie. Volume 6. Electromagnétisme. Edité par Douglas Figueroa (USB).
- Giancoli, D. 2006. Physique: principes avec applications. 6e. Salle des Prentices Ed.
- Serway, R., Jewett, J. 2008. Physique pour la science et l'ingénierie. Volume 1. 7e. Éd. Cengage Learning.



Personne n'a encore commenté ce post.