Réduction des termes similaires (avec exercices résolus)

La réduction de termes similaires est une méthode utilisée pour simplifier les expressions algébriques. Dans une expression algébrique, les termes semblables sont ceux qui ont la même variable; c'est-à-dire qu'ils ont les mêmes inconnues représentées par une lettre, et ceux-ci ont les mêmes exposants.

Dans certains cas, les polynômes sont extensifs, et pour arriver à une solution, il faut essayer de réduire l'expression; Cela est possible lorsqu'il existe des termes similaires, qui peuvent être combinés en appliquant des opérations et des propriétés algébriques telles que l'addition, la soustraction, la multiplication et la division..

Index des articles

• 1 Explication
• 2 Comment faire une réduction de termes similaires?
  • 2.1 Exemple
  • 2.2 Réduction de termes similaires avec des signes égaux
  • 2.3 Réduction de termes similaires avec des signes différents
• 3 Réduction des conditions similaires dans les opérations
  • 3.1 En sommes
  • 3.2 En soustraction
  • 3.3 En multiplication
  • 3.4 Dans les divisions
• 4 exercices résolus
  • 4.1 Premier exercice
  • 4.2 Deuxième exercice
• 5 Références

Explication

Des termes similaires sont formés par les mêmes variables avec les mêmes exposants, et dans certains cas, ceux-ci ne sont différenciés que par leurs coefficients numériques.

Les termes similaires sont également considérés comme ceux qui n'ont pas de variables; c'est-à-dire les termes qui n'ont que des constantes. Ainsi, par exemple, les termes suivants sont comme des termes:

- 6x^deux - 3x^deux. Les deux termes ont la même variable x^deux.

- 4e^deuxb³ + 2e^deuxb³. Les deux termes ont les mêmes variables a^deuxb³.

- 7 - 6. Les termes sont constants.

Les termes qui ont les mêmes variables mais avec des exposants différents sont appelés termes différents, tels que:

- 9a^deuxb + 5ab. Les variables ont des exposants différents.

- 5x + et. Les variables sont différentes.

- b - 8. Un terme a une variable, l'autre est une constante.

En identifiant les termes similaires qui forment un polynôme, ceux-ci peuvent être réduits à un, combinant tous ceux qui ont les mêmes variables avec les mêmes exposants. De cette manière, l'expression est simplifiée en réduisant le nombre de termes qui la composent et le calcul de sa solution est facilité..

Comment faire une réduction de termes similaires?

La réduction de termes similaires se fait en appliquant la propriété associative d'addition et la propriété distributive du produit. En utilisant la procédure suivante, vous pouvez effectuer une réduction de terme:

- Les termes similaires sont regroupés en premier.

- Les coefficients (les nombres qui accompagnent les variables) des termes similaires sont ajoutés ou soustraits, et les propriétés associatives, commutatives ou distributives sont appliquées, selon le cas..

- Puis les nouveaux termes obtenus sont écrits en plaçant devant eux le signe résultant de l'opération.

Exemple

Réduisez les termes de l'expression suivante: 10x + 3y + 4x + 5y.

Solution

Premièrement, les termes sont ordonnés pour regrouper ceux qui sont similaires, en appliquant la propriété commutative:

10x + 3y + 4x + 5y = 10x + 4x + 3y + 5y.

Ensuite, la propriété distributive est appliquée et les coefficients qui accompagnent les variables sont ajoutés pour obtenir la réduction des termes:

10x + 4x + 3 ans + 5 ans

= (10 + 4) x + (3 + 5) y

= 14x + 8 ans.

Pour réduire des termes similaires, il est important de prendre en compte les signes des coefficients qui accompagnent la variable. Il existe trois cas possibles:

Réduction des termes similaires avec des signes égaux

Dans ce cas, les coefficients sont ajoutés et le signe des termes est placé devant le résultat. Par conséquent, s'ils sont positifs, les termes résultants seront positifs; dans le cas où les termes sont négatifs, le résultat aura le signe (-) accompagné de la variable. Par exemple:

a) 22ab^deux + 12ab^deux = 34 ab^deux.

b) -18x³ - 9x³ - 6 = -27x³ - 6.

Réduction des termes similaires csur différents signes

Dans ce cas, les coefficients sont soustraits et le signe du plus grand coefficient est placé devant le résultat. Par exemple:

a) 15x^deuxy - 4x^deuxet + 6x^deuxy - 11x^deuxOui

= (15x^deuxet + 6x^deuxy) + (- 4x^deuxy - 11x^deuxY)

= 21x^deuxy + (-15x^deuxY)

= 21x^deuxy - 15x^deuxOui

= 6x^deuxOui.

b) -5a³b + 3 a³b - 4a³b + a³b

= (3 à³b + a³b) + (-5a³b - 4a³b)

= 4a³b - 9a³b

= -5 à³b.

Ainsi, pour réduire les termes similaires qui ont des signes différents, un seul terme additif est formé avec tous ceux qui ont un signe positif (+), les coefficients sont ajoutés et le résultat est accompagné des variables.

De la même manière, un terme soustractif est formé, avec tous les termes qui ont un signe négatif (-), les coefficients sont ajoutés et le résultat est accompagné des variables.

Enfin, les sommes des deux termes formés sont soustraites, et le signe du plus grand est placé du résultat.

Réduction des conditions similaires dans les opérations

La réduction de termes similaires est une opération d'algèbre, qui peut être appliquée en addition, soustraction, multiplication et division algébrique.

En sommes

Lorsque vous avez plusieurs polynômes avec des termes similaires, pour les réduire, les termes de chaque polynôme sont ordonnés en gardant leurs signes, puis ils sont écrits les uns après les autres et les termes similaires sont réduits. Par exemple, nous avons les polynômes suivants:

3x - 4xy + 7x^deuxet + 5xy^deux.

- 6x^deuxy - 2xy + 9 xy^deux - 8x.

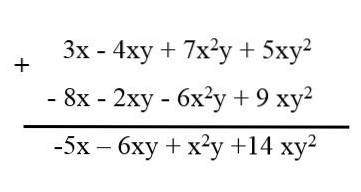
En soustraction

Pour soustraire un polynôme d'un autre, le minuend est écrit, puis le sous-trait avec ses signes modifiés, puis la réduction des termes similaires est effectuée. Par exemple:

5e³ - 3ab^deux + 3b^deuxc

6ab^deux + 2e³ - 8b^deuxc

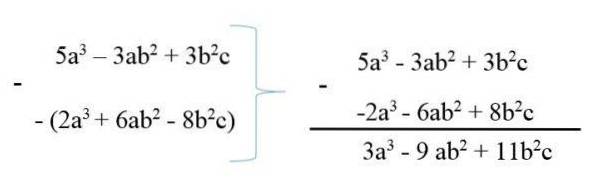
Ainsi, les polynômes sont résumés en 3a³ - 9ab^deux + 11b^deuxc.

Dans les multiplications

Dans un produit de polynômes, les termes qui composent le multiplicande sont multipliés par chaque terme qui compose le multiplicateur, en considérant que les signes de la multiplication restent les mêmes s'ils sont positifs.

Ils ne seront modifiés que lorsqu'ils seront multipliés par un terme négatif; c'est-à-dire que lorsque deux termes du même signe sont multipliés, le résultat sera positif (+), et lorsqu'ils ont des signes différents, le résultat sera négatif (-).

Par exemple:

a) (a + b) _* (a + b)

= a^deux + ab + ab + b^deux

= a^deux + 2ab + b^deux.

b) (a + b) _* (un B)

= a^deux - ab + ab - b^deux

= a^deux - b^deux.

taxi) _* (un B)

= a^deux - ab - ab + b^deux

= a^deux - 2ab + b^deux.

Dans les divisions

Lorsque vous souhaitez réduire deux polynômes via une division, vous devez trouver un troisième polynôme qui, multiplié par le deuxième (diviseur), donne le premier polynôme (dividende).

Pour cela, les termes du dividende et du diviseur doivent être ordonnés, de gauche à droite, afin que les variables des deux soient dans le même ordre.

Ensuite, la division est effectuée, à partir du premier terme à gauche du dividende par le premier terme à gauche du diviseur, en tenant toujours compte des signes de chaque terme.

Par exemple, réduisez le polynôme: 10x⁴ - 48x³et + 51x^deuxOui^deux + 4xy³ - 15 ans⁴ en le divisant par le polynôme: -5x^deux + 4xy + 3y^deux.

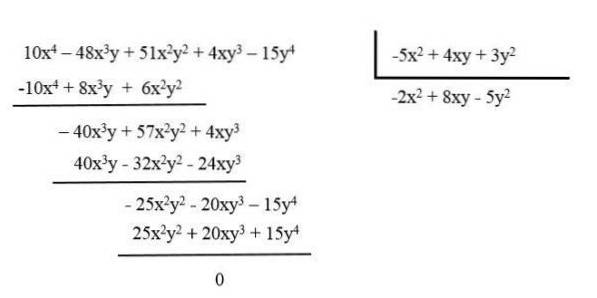
Le polynôme résultant est -2x^deux + 8xy - 5 ans^deux.

Exercices résolus

Premier exercice

Réduisez les termes de l'expression algébrique donnée:

15e^deux - 8ab + 6a^deux - 6ab - 9 + 4a^deux - 13 ab.

Solution

La propriété commutative d'addition est appliquée, regroupant les termes qui ont les mêmes variables:

15e^deux - 8ab + 6a^deux - 6ab + 9 + 4a^deux - 13

= (15a^deux + 6e^deux + 4e^deux) + (- 8ab - 6ab) + (9-13).

Ensuite, la propriété distributive de multiplication est appliquée:

15e^deux - 8ab + 6a^deux - 6ab + 9 + 4a^deux - 13

= (15 + 6 + 4) a^deux + (- 8 - 6) ab + (9 - 13).

Enfin, ils sont simplifiés en ajoutant et en soustrayant les coefficients de chaque terme:

15e^deux - 8ab + 6a^deux - 6ab + 9 + 4a^deux - 13

= 25a^deux - 14ab - 4.

Deuxième exercice

Simplifiez le produit des polynômes suivants:

(8x³ + 7xy^deux)_*(8x³ - 7 xy^deux).

Solution

Chaque terme du premier polynôme est multiplié par le second, en tenant compte du fait que les signes des termes sont différents; par conséquent, le résultat de sa multiplication sera négatif, ainsi que les lois des exposants doivent être appliquées.

(8x³ + 7xy^deux) _* (8x³ - 7xy^deux)

= 64 x⁶ - 56 x³_* xy^deux + 56 x³_* xy^deux - 49 x^deuxOui⁴

= 64 x⁶ - 49 x^deuxOui⁴.

Les références

1. Angel, A. R. (2007). Algèbre élémentaire. Éducation Pearson,.
2. Baldor, A. (1941). Algèbre. La Havane: Culture.
3. Jerome E. Kaufmann, K. L. (2011). Algèbre élémentaire et intermédiaire: une approche combinée. Floride: Cengage Learning.
4. Smith, S. A. (2000). Algèbre. Éducation Pearson.
5. Vigil, C. (2015). Algèbre et ses applications.