La relation mathématique est le lien qui existe entre les éléments d'un sous-ensemble par rapport au produit de deux ensembles. Ongle une fonction implique l'opération mathématique pour déterminer la valeur d'une variable dépendante en fonction de la valeur d'une variable indépendante. Chaque fonction est une relation mais toutes les relations ne sont pas une fonction.
| Relation | Une fonction | |
|---|---|---|
| Définition | Sous-ensemble de paires ordonnées qui correspondent au produit cartésien de deux ensembles. | Opération mathématique à effectuer avec la variable X pour obtenir la variable Oui. |
| Notation | X R Oui; X c'est lié à Oui. | Oui= ƒ (X); Oui est une fonction de X. |
| Caractéristiques |
|
|
| Exemples |
|
|
On l'appelle la relation binaire d'un ensemble A dans un ensemble B ou la relation entre les éléments de A et B à chaque sous-ensemble C du produit cartésien A x B.
Autrement dit, si l'ensemble A est composé des éléments 1, 2 et 3, et l'ensemble B est composé des éléments 4 et 5, le produit cartésien de A x B sera les paires ordonnées:
A x B = (1,4), (2,4), (3, 4), (1,5), (2,5), (3,5).
Le sous-ensemble C = (2,4), (3,5) sera une relation de A et B puisqu'il est composé des paires ordonnées (2,4) et (3, 5), le résultat du cartésien produit de A x B.
"Soit A et B deux ensembles non vides quelconques, soit A x B l'ensemble produit des deux, c'est-à-dire: A x B est formé par les paires ordonnées (x, y) telles que X est l'élément de A et Oui c'est pour B.Si un sous-ensemble C est défini dans A x B, une relation binaire dans A et B est automatiquement déterminée comme suit:
X R Oui si et seulement si (x, y) ∈ C
(la notation X R Oui Moyens "X c'est lié à Oui").
Nous appellerons l'ensemble A set de départ et nous appellerons l'ensemble B ensemble d'arrivée.
le domaine de relation sont les éléments qui composent le set de départ, tandis que les gamme de rapport sont les éléments du set d'arrivée.
Ensemble À de X éléments des hommes dans une population et B est l'ensemble des Oui éléments de femmes de la même population. Une relation est établie lorsque "X il est marié avec Oui".
Lorsque nous parlons d'une fonction mathématique d'un ensemble A dans un ensemble B, nous nous référons à une règle ou un mécanisme qui relie les éléments de l'ensemble A à un élément de l'ensemble B.
"Sean X Oui Oui deux vraies variables, on dit alors que y est une fonction de x oui à chaque valeur que je prends X correspond à une valeur de Oui."
La variable indépendante est X tandis que Oui est la variable dépendante ou la fonction:
y = ƒ (x)
L'ensemble dans lequel le X est appelé domaine de la fonction (original) et la variation de Oui gamme de fonctions (photo).
L'ensemble des paires (X, Oui) tel que Oui= ƒ (X) est appelé graphe de fonction; s'ils sont représentés en axes cartésiens, on obtient une famille de points appelée graphe de fonction.
En mathématiques, nous obtenons de nombreux exemples de fonctions. Voici des exemples de fonctions phares.
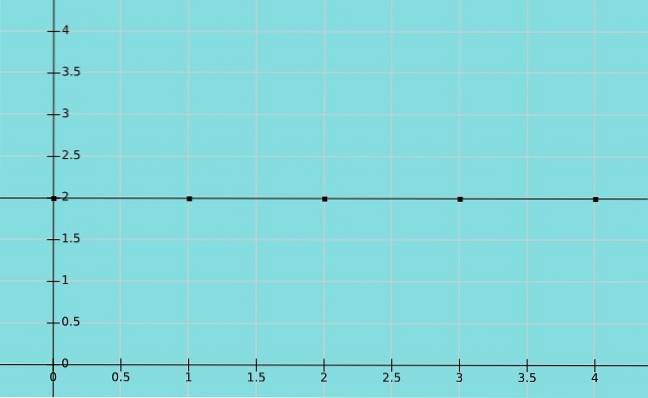
Une fonction est appelée constante si l'élément de l'ensemble B qui correspond à l'ensemble A est le même. Dans ce cas, toutes les valeurs de x correspondent à la même valeur de y. Ainsi, le domaine est les nombres réels tandis que la plage est une valeur constante.
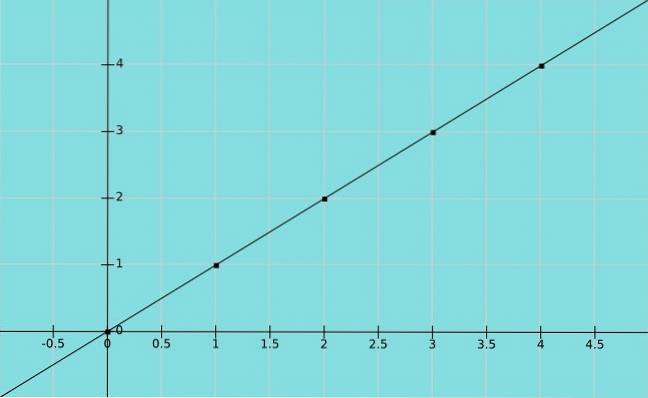
Supposons X est une variable et que Oui prend la même valeur que X. On a alors une fonction d'identité y = x, où les pairesx, y) dans le graphique sont (1,1), (2,2), (3,3) et ainsi de suite.
Une fonction polynomiale remplit la forme y = anXn+àn-1+Xn-1+… + AdeuxXdeux+à1x + a0. Le graphique ci-dessus montre la fonction ƒ (x) = xdeux+x-2.
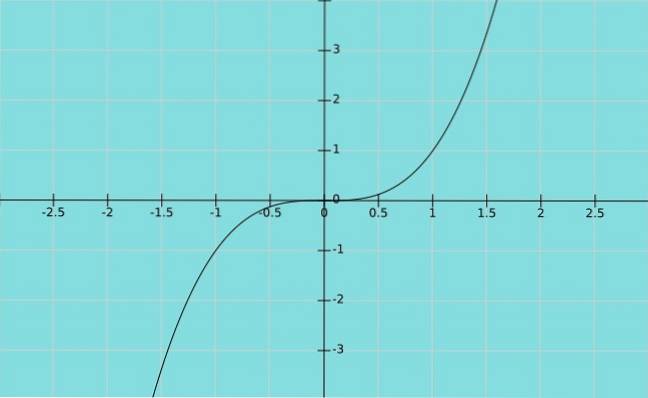
Supposons maintenant que la variable dépendante Oui égale la variable indépendante X élevé au cube. Nous avons la fonction y = x3, dont le graphique est présenté ci-dessous:
Personne n'a encore commenté ce post.