
Explication de la deuxième condition d'équilibre, exemples, exercices
La deuxième condition d'équilibre établit que la somme des couples ou moments produits par toutes les forces agissant sur un corps, quel que soit le point où elles sont calculées, doit être annulée pour que ledit corps soit en équilibre statique ou dynamique.
Dénotant le couple ou le moment de force par la lettre grecque τ, mathématiquement, il est exprimé comme ceci:
∑ τ = 0

La lettre en gras indique la nature vectorielle du moment, qui doit être annulée par rapport à tout point choisi comme centre de rotation. De cette manière, l'annulation du couple net garantit que l'objet ne commence pas à tourner ou à basculer..
Cependant, si l'objet tournait déjà auparavant et que le couple net disparaît soudainement, la rotation se poursuivra, mais à vitesse angulaire constante.
La deuxième condition d'équilibre est utilisée en conjonction avec la première condition, qui dit que la somme des forces sur un corps doit être nulle, pour qu'elle ne se traduise pas, ou que si elle le fait, c'est avec un mouvement rectiligne uniforme:
∑ F = 0
Les deux conditions s'appliquent aux corps étendus, ceux dont les dimensions sont mesurables. Quand un objet est supposé être une particule, cela n'a aucun sens de parler de rotations, et la première condition est suffisante pour garantir l'équilibre.
Exemples
La deuxième condition d'équilibre se révèle dans d'innombrables situations:
En grimpant à l'échelle
Lors du support d'une échelle sur le sol et le mur, nous avons besoin de suffisamment de friction, en particulier sur le sol, pour garantir que l'échelle ne glisse pas. Si nous essayons de grimper sur une échelle appuyée sur un sol huileux, mouillé ou glissant, il n'est pas difficile d'anticiper que nous allons tomber.
Pour pouvoir utiliser l'échelle en toute confiance, il est nécessaire qu'elle soit en équilibre statique lors de la montée et lorsqu'elle se trouve sur l'échelon requis.
Déplacer un placard
Lorsque vous souhaitez déplacer un meuble haut comme un placard, ou tout meuble dont la hauteur est supérieure à sa largeur, il est pratique de pousser sur un point bas, pour éviter de basculer, de cette manière il est plus probable que le les meubles glisseront au lieu de tourner et s'allongeront.
Dans de telles circonstances, le meuble n'est pas nécessairement en équilibre, car il pourrait se déplacer rapidement, mais au moins il ne se renverserait pas.
Balcons
Les balcons qui dépassent des bâtiments doivent être construits de manière à ce que même s'il y a beaucoup de monde sur le dessus, ils ne basculent pas et ne s'effondrent pas.
Diélectriques dans les champs électriques externes
En plaçant un matériau diélectrique dans un champ électrique externe, les molécules se déplacent et tournent jusqu'à adopter une position d'équilibre, créant un champ électrique à l'intérieur du matériau..
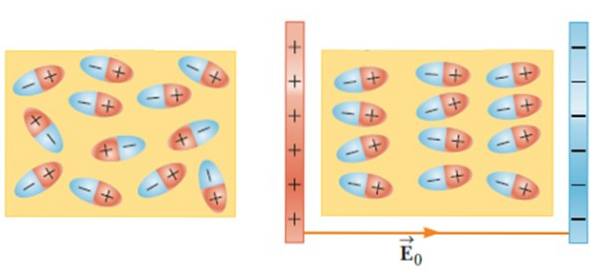
Cet effet augmente la capacité d'un condensateur lorsqu'un matériau tel que du verre, du caoutchouc, du papier ou de l'huile est inséré entre ses cadres..
Signes et lampes
Il est courant que de nombreux habitants accrochent des affiches sur le mur du bâtiment, afin qu'elles soient visibles des passants..
L'affiche est maintenue par une barre et un câble, tous deux fixés au mur par des supports. Les différentes forces qui agissent doivent assurer que l'affiche ne tombe pas, pour laquelle les deux conditions d'équilibre entrent en jeu.
Un réflecteur peut également être placé de cette manière dans un parc, comme sur la figure suivante:
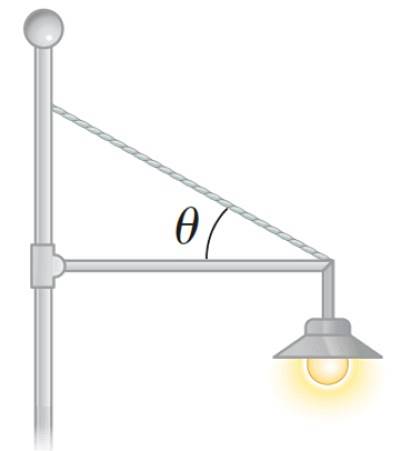
Comment calculer le couple net ou le moment net d'une force?
Le couple ou le moment d'une force, désigné par τ ou alors M dans certains textes, il est toujours calculé par rapport à un point où passe l'axe de rotation.
Il est défini comme le produit vectoriel entre le vecteur de position r, qui est dirigé depuis ledit axe vers le point d'application de la force et de la force F:
τ = r × F
Étant un vecteur, il est nécessaire d'exprimer le couple en donnant sa grandeur, sa direction et son sens. La grandeur est donnée par:
τ = rF.sen θ
Règle de la main droite pour le produit vectoriel
Lorsque le problème est dans le plan, la direction du couple est perpendiculaire au papier ou à l'écran, et la direction est déterminée par la règle de la main droite, dans laquelle l'index pointe vers r, majeur vers F et le pouce pointe dans ou hors du papier.
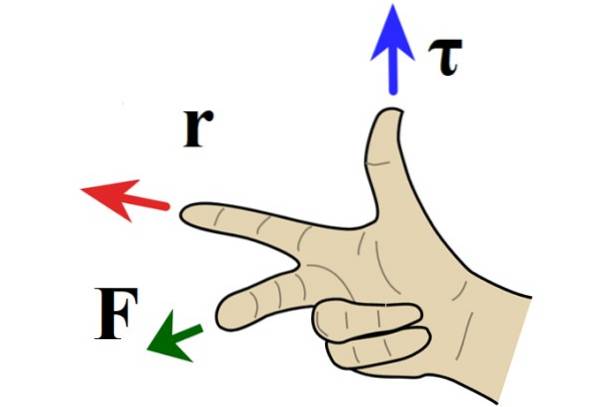
Lorsque le couple pointe hors du papier, la rotation se fait dans le sens antihoraire et se voit attribuer un signe positif par convention. Si au contraire le couple est dirigé vers l'intérieur de la lame, la rotation est dans le sens des aiguilles d'une montre et négative..
Pour trouver le couple net, un point approprié est choisi pour le calcul, qui peut être celui auquel la plus grande quantité de forces agit. Dans ce cas, le moment de ces forces est nul, car il a un vecteur de position r de grandeur 0.
Vous pouvez choisir n'importe quel point offrant suffisamment d'informations pour résoudre l'inconnu qui demande la résolution du problème. Voyons cela plus en détail ci-dessous.
Exercice résolu
Le réflecteur de la figure suivante a une masse de 20 kg et est supporté par une fine barre horizontale, de masse et de longueur L négligeables, qui est articulée sur un poteau. Le câble, également léger, qui aide à soutenir le réflecteur forme un angle θ = 30º avec la barre. Calculer:
a) La tension dans le câble
b) L'amplitude de la force F exercée par le montant sur la barre à travers la charnière.
Solution
Nous appliquerons la première condition d'équilibre ∑ F = 0 aux forces indiquées dans le diagramme:
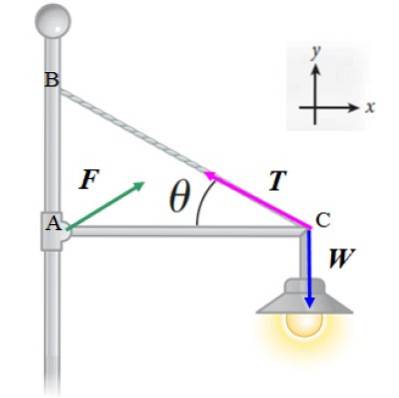
F + T + W = 0
Notez que la magnitude et la direction de F sont encore à déterminer, mais nous supposons qu'il comporte deux composantes: FX et FOui. De cette façon, nous obtenons deux équations:
FX -T. cos θ = 0
FOui - W + T⋅ sin θ = 0
Appliquons maintenant la deuxième condition d'équilibre, en choisissant le point A, puisque nous ne connaissons pas la magnitude de F ni celui de T. En choisissant ce point, le vecteur rÀ est nul, donc le moment de F est nul et la magnitude de F n'apparaîtra pas dans l'équation:
-W⋅L + T⋅sen θ⋅L = 0
Donc:
T.sen θ.L = W.L
T = W / sin θ = (20 kg x 9,8 m / sdeux) / Sin 30º = 392 N
Connaissant la grandeur de T, nous pouvons résoudre le composant FX:
FX = T⋅ cos θ = 392 cos 30º N = 339. 5 N
Et puis le composant FOui:
FOui = W - T⋅ sin θ = (20 kg x 9,8 m / sdeux) - 392⋅sin 30º = 0
Ensuite, nous pouvons exprimer F Donc:
F = 339,5 N X
C'est donc une force horizontale. En effet, nous avons considéré que la barre avait un poids négligeable.
Si le point C avait été choisi pour calculer le moment résultant, les vecteurs rT Oui rW sont nulles, donc:
M = FetL = 0
On en conclut que FOui = 0. De cette manière:
- W + T⋅ sin θ = 0
T = W / sin θ
Quel est le même résultat obtenu initialement lors du choix du point A comme lieu de passage de l'axe de rotation.
Thèmes d'intérêt
Conditions d'équilibre.
Première condition d'équilibre.
Les références
- Bedford, 2000. A. Mécanique du génie: statique. Addison Wesley.
- Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 4. Systèmes de particules. Edité par Douglas Figueroa (USB).
- Giancoli, D. 2006. Physique: principes avec applications. 6e. Salle des Prentices Ed.
- Sears, Zemansky. 2016. Physique universitaire et physique moderne. 14e. Éd. Volume 1.
- Serway, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Éd. Cengage Learning.


Personne n'a encore commenté ce post.