
Méthode et exemple de lissage exponentiel
le lissage exponentiel c'est une manière de prévoir la demande d'un article pour une période donnée. Cette méthode estime que la demande sera égale à la moyenne de la consommation historique sur une période donnée, donnant un poids ou un poids plus important aux valeurs plus proches dans le temps. De plus, pour les prévisions suivantes, tenez compte de l'erreur existante de la prévision actuelle.
La prévision de la demande est la méthode de projection de la demande des clients pour un produit ou un service. Ce processus est continu, où les responsables utilisent des données historiques pour calculer ce à quoi ils s'attendent de la demande de vente pour un bien ou un service..
Les informations du passé de l'entreprise sont utilisées en les ajoutant aux données économiques du marché pour voir si les ventes augmenteront ou diminueront.
Les résultats de la prévision de la demande sont utilisés pour fixer des objectifs pour le service commercial, en essayant de rester en ligne avec les objectifs de l'entreprise.
Index des articles
- 1 Méthode de lissage exponentiel
- 1.1 Lissage dans la prévision
- 1.2 Moyenne mobile pondérée
- 1.3 Lissage exponentiel
- 2 Exemple
- 3 Références
Méthode de lissage exponentiel
Le lissage est un processus statistique très courant. Les données lissées se retrouvent souvent dans diverses formes de la vie quotidienne. Chaque fois qu'une moyenne est utilisée pour décrire quelque chose, un nombre lissé est utilisé.
Supposons que l'hiver le plus chaud jamais enregistré ait été connu cette année. Pour le quantifier, nous commençons par l'ensemble des données de température quotidiennes pour la période hivernale de chaque année historique enregistrée..
Cela génère un certain nombre de nombres avec de grands «sauts». Vous avez besoin d'un nombre qui élimine tous ces sauts des données pour pouvoir comparer plus facilement un hiver à un autre.
L'élimination du saut dans les données s'appelle le lissage. Dans ce cas, une moyenne simple peut être utilisée pour obtenir un lissage.
Lissage dans les prévisions
Pour prévoir la demande, le lissage est également utilisé pour éliminer les variations de la demande historique. Cela permet une meilleure identification des modèles de demande, qui peuvent être utilisés pour estimer la demande future..
Les variations de la demande sont le même concept que le «saut» des données de température. La manière la plus courante d'éliminer les variations de l'historique de la demande consiste à utiliser une moyenne, ou plus précisément une moyenne mobile..
La moyenne mobile utilise un nombre prédéfini de périodes pour calculer la moyenne, et ces périodes se déplacent avec le temps..
Par exemple, si une moyenne mobile sur quatre mois est utilisée et qu'aujourd'hui est le 1er mai, la demande moyenne pour janvier, février, mars et avril sera utilisée. Le 1er juin, la demande de février, mars, avril et mai sera utilisée.
Moyenne mobile pondérée
Lorsque vous utilisez une moyenne simple, la même importance est appliquée à chaque valeur de l'ensemble de données. Par conséquent, dans une moyenne mobile sur quatre mois, chaque mois représente 25% de la moyenne mobile..
En utilisant l'historique de la demande pour projeter la demande future, il va de soi que la période la plus récente a un impact plus important sur les prévisions..
Vous pouvez adapter le calcul de la moyenne mobile pour appliquer différents «poids» à chaque période, afin d'obtenir les résultats souhaités..
Ces poids sont exprimés en pourcentages. Le total de tous les poids pour toutes les périodes doit s'élever à 100%.
Par conséquent, si vous souhaitez appliquer 35% comme poids pour la période la plus proche dans la moyenne pondérée sur quatre mois, vous pouvez soustraire 35% de 100%, laissant 65% à diviser entre les trois périodes restantes.
Par exemple, vous pouvez vous retrouver avec une pondération de 15%, 20%, 30% et 35% respectivement pour les quatre mois (15 + 20 + 30 + 35 = 100).
Lissage exponentiel
L'entrée de commande pour le calcul de lissage exponentiel est connue sous le nom de facteur de lissage. Représente le poids appliqué à la demande pour la période la plus récente.
Si 35% est utilisé comme pondération de période la plus récente dans le calcul de la moyenne mobile pondérée, vous pouvez également choisir d'utiliser 35% comme facteur de lissage dans le calcul de lissage exponentiel..
Partie exponentielle
La différence dans le calcul du lissage exponentiel est qu'au lieu d'avoir à déterminer le poids à appliquer à chaque période précédente, le facteur de lissage est utilisé pour le faire automatiquement..
C'est la partie "exponentielle". Si 35% est utilisé comme facteur de lissage, le poids de la demande pour la période la plus récente sera de 35%. La pondération de la demande de la période précédente à la plus récente sera de 65% de 35%.
65% provient de la soustraction de 35% à 100%. Cela équivaut à une pondération de 22,75% pour cette période. La demande de la prochaine période la plus récente sera de 65% de 65% à 35%, ce qui équivaut à 14,79%.
La période précédente sera pondérée comme 65% de 65% de 65% de 35%, soit 9,61%. Cela sera fait pour toutes les périodes précédentes, jusqu'à la première période.
Formule
La formule de calcul du lissage exponentiel est la suivante: (D * S) + (P * (1-S)), où,
D = demande la plus récente de la période.
S = facteur de lissage, représenté sous forme décimale (35% serait 0,35).
P = prévision de la période la plus récente, résultat du calcul de lissage de la période précédente.
En supposant que nous ayons un facteur de lissage de 0,35, nous aurions alors: (D * 0,35) + (P * 0,65).
Comme vous pouvez le voir, les seules entrées de données requises sont la demande et la prévision de la période la plus récente..
Exemple
Une compagnie d'assurance a décidé d'étendre son marché à la plus grande ville du pays, en fournissant une assurance pour les véhicules.
Dans un premier temps, l'entreprise souhaite prévoir le montant de l'assurance automobile que les habitants de cette ville souscriront.
Pour ce faire, ils utiliseront comme données initiales le montant de l'assurance automobile souscrite dans une autre petite ville..
La demande prévue pour la période 1 est de 2869 assurances véhicules sous contrat, mais la demande réelle au cours de cette période était de 3200..
À la discrétion de l'entreprise, elle attribue un facteur de lissage de 0,35. La demande prévue pour la période suivante est: P2 = (3200 * 0,35) + 2869 * (1-0,35) = 2984,85.
Ce même calcul a été fait pour toute l'année, obtenant le tableau comparatif suivant entre ce qui a été réellement obtenu et ce qui était prévu pour ce mois.
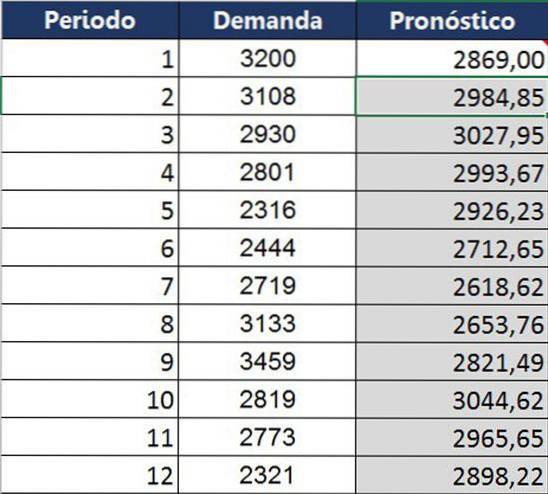
Par rapport aux techniques de moyennage, le lissage exponentiel peut mieux prédire la tendance. Cependant, il est toujours insuffisant, comme le montre le graphique:
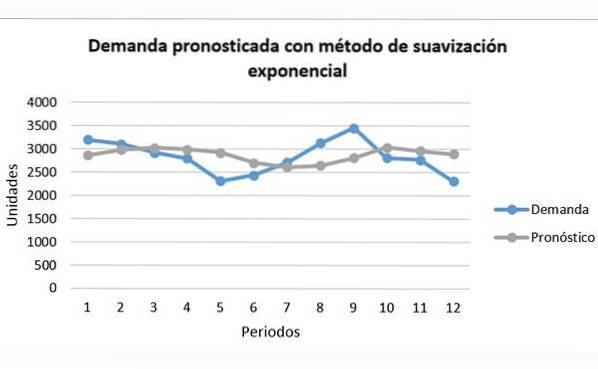
On peut voir comment la ligne grise de la prévision peut être bien en dessous ou au-dessus de la ligne bleue de la demande, sans pouvoir la suivre pleinement.
Les références
- Wikipédia (2019). Lissage exponentiel. Tiré de: es.wikipedia.org.
- Ingenio Empresa (2016). Comment utiliser le lissage exponentiel simple pour prévoir la demande. Tiré de: ingenioempresa.com.
- Dave Piasecki (2019). Lissage exponentiel expliqué. Tiré de: inventaireops.com.
- Étude (2019). Techniques de prévision de la demande: moyenne mobile et lissage exponentiel. Tiré de: study.com.
- Cityu (2019). Méthodes de lissage exponentiel. Tiré de: personal.cb.cityu.edu.hk.



Personne n'a encore commenté ce post.