
Histoire de la somme de Riemann, formules et propriétés, exercices
La Somme de Riemann est le nom donné au calcul approché d'une intégrale définie, au moyen d'une sommation discrète avec un nombre fini de termes. Une application courante est l'approximation de la zone de fonctions sur un graphe.
C'est le mathématicien allemand Georg Friedrich Bernhard Riemann (1826-1866) qui a le premier proposé une définition rigoureuse de l'intégrale d'une fonction dans un intervalle donné. Il l'a fait savoir dans un article publié en 1854.
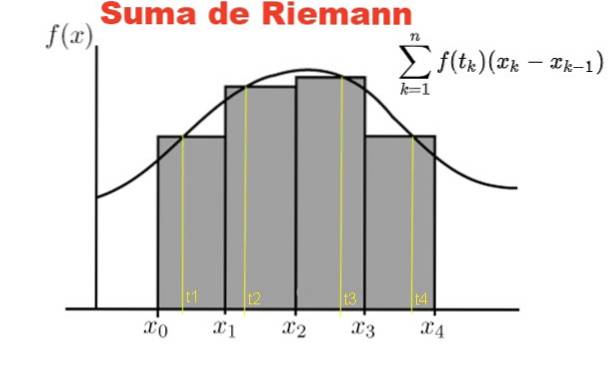
La somme de Riemann est définie sur une fonction y = f (x), avec x appartenant à l'intervalle fermé [a, b]. Sur cet intervalle une partition P de n éléments est faite:
P = x0= a, x1, Xdeux,..., Xn= b
Cela signifie que l'intervalle est divisé comme suit:

Xk-1 ≤ tk ≤ xk
La figure 1 montre graphiquement la somme de Riemann de la fonction f sur l'intervalle [x0, X4] sur une partition de quatre sous-intervalles, les rectangles gris.
La somme représente l'aire totale des rectangles et le résultat de cette somme se rapproche numériquement de l'aire sous la courbe f, entre l'abscisse x = x0 y x = x4.
Bien entendu, l'approximation de l'aire sous la courbe s'améliore considérablement à mesure que le nombre n les partitions est plus grande. De cette façon, la somme converge vers l'aire sous la courbe, lorsque le nombre n des partitions tend vers l'infini.
Index des articles
- 1 Formules et propriétés
- 1.1 L'aire sous la courbe
- 2 exercices résolus
- 2.1 - Exercice 1
- 2.2 - Exercice 2
- 3 Références
Formules et propriétés
La somme de Riemann de la fonction f (x) sur la partition:
P = x0= a, x1, Xdeux,..., Xn= b
Défini sur l'intervalle [a, b], il est donné par:
S (P, f) = ∑k = 1n f (tk) (Xk - Xk-1)
Où Tk est une valeur sur l'intervalle [xk, Xk-1]. Dans la somme de Riemann, des intervalles réguliers de largeur Δx = (b - a) / n sont généralement utilisés, où a et b sont les valeurs minimale et maximale de l'abscisse, tandis que n est le nombre de subdivisions.
Dans ce cas, le Somme droite de Riemann c'est:
Sd (f, n) = [f (a + Δx) + f (a + 2Δx) +… + f (a + (n-1) Δx) + f (b)] * Δx
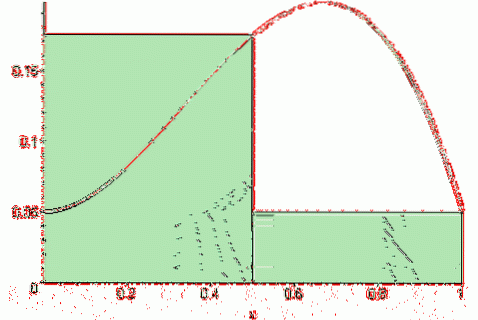
Tandis que le Riemann a laissé la somme s'exprime comme:
Si (f, n) = [f (a) + f (a + Δx) +… + f (a + (n-1) Δx)] * Δx
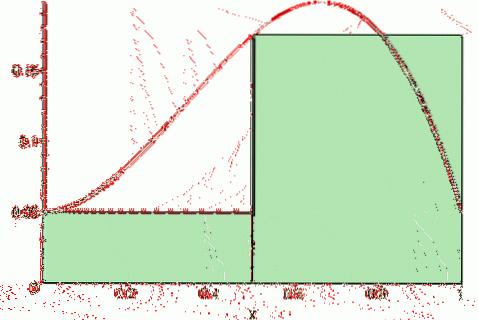
Finalement, le somme de Riemann centrale c'est:
Sc (f, n) = [f (a + Δx / 2) + f (a + 3Δx / 2) +… + f (b- Δx / 2)] * Δx
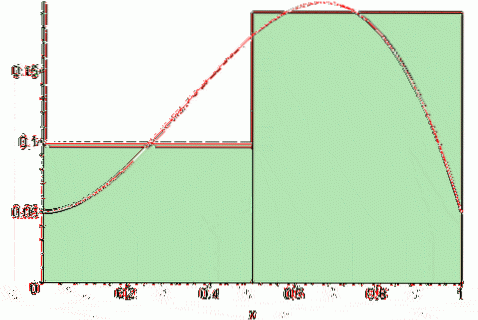
En fonction de l'emplacement du point tk sur l'intervalle [xk, Xk-1] la somme de Riemann peut surestimer ou sous-estimer la valeur exacte de l'aire sous la courbe de la fonction y = f (x). En d'autres termes, les rectangles peuvent dépasser de la courbe ou être légèrement en dessous..
L'aire sous la courbe
La propriété principale de la somme de Riemann et dont découle son importance, est que si le nombre de subdivisions tend vers l'infini, le résultat de la somme converge vers l'intégrale définie de la fonction:

Exercices résolus
- Exercice 1
Calculez la valeur de l'intégrale définie entre a = -2 à b = +2 de la fonction:
f (x) = xdeux
Utilisez une somme de Riemann. Pour ce faire, trouvez d'abord la somme pour n partitions régulières de l'intervalle [a, b] puis prenez la limite mathématique pour le cas où le nombre de partitions tend vers l'infini.
Solution
Voici les étapes à suivre:
-Tout d'abord, définissez l'intervalle des partitions comme suit:
Δx = (b - a) / n.
-Alors la somme de Riemann de la droite correspondant à la fonction f (x) ressemble à ceci:


[-2 + (4i / n)]deux = 4 - (16 i / n) + (4 / n)deux jedeux
-Et puis il est soigneusement substitué dans la sommation:

-L'étape suivante consiste à séparer les sommations et à prendre les quantités constantes comme facteur commun de chaque somme. Il faut tenir compte du fait que l'indice est i, donc les nombres et les termes avec n sont considérés comme constants:

-Chaque sommation est évaluée, car pour chacune d'elles il existe des expressions appropriées. Par exemple, la première des sommes donne n:



S (f, n) = 16 - 64 (n + 1) / 2n + 64 (n + 1) (2n + 1) / 6ndeux
-Enfin, nous avons que l'intégrale que nous voulons calculer est:

= 16 - (64/2) + (64/3) = 16/3 = 5 333
Le lecteur peut vérifier qu'il s'agit du résultat exact, qui peut être obtenu en résolvant l'intégrale indéfinie et en évaluant les limites d'intégration par la règle de Barrow.
- Exercice 2
Déterminez approximativement la zone sous la fonction:
f (x) = (1 / √ (2π)) e(-Xdeux/deux)
Entrez x = -1 et x = + 1, en utilisant une somme de Riemann centrale avec 10 partitions. Comparez avec le résultat exact et estimez la différence en pourcentage.
Solution
Le pas ou incrément entre deux valeurs discrètes successives est:
Δx = (1 - (-1) / 10 = 0,2
Ainsi, la partition P sur laquelle les rectangles sont définis ressemble à ceci:
P = -1,0; -0,8; -0,6; -0,4; -0,2; 0,0; 0,2; 0,4; 0,6; 0,8; 1,0
Mais comme on veut la somme centrale, la fonction f (x) sera évaluée aux milieux des sous-intervalles, c'est-à-dire dans l'ensemble:
T = -0,9; -0,7; -0,5; -0,3; -0,1; 0,1; 0,3; 0,5; 0,7; 0,9.
La somme (centrale) de Riemann ressemble à ceci:
S = f (-0,9) * 0,2 + f (-0,7) * 0,2 + f (-0,5) * 0,2 +… + f (0,7) * 0,2 + f (0,9) * 0,2
La fonction f étant symétrique, il est possible de réduire la somme à seulement 5 termes et le résultat est multiplié par deux:
S = 2 * 0,2 * f (0,1) + f (0,3) + f (0,5) + f (0,7) + f (0,9)
S = 2 * 0,2 * 0,397+ 0,381+ 0,352+ 0,312+ 0,266 = 0,683
La fonction donnée dans cet exemple n'est autre que la cloche gaussienne bien connue (normalisée, avec une moyenne égale à zéro et un écart type un). L'aire sous la courbe dans l'intervalle [-1,1] pour cette fonction est de 0,6827.

Cela signifie que la solution approximative avec seulement 10 termes correspond à la solution exacte à trois décimales. Le pourcentage d'erreur entre l'intégrale approximative et exacte est de 0,07%.
Les références
- Casteleiro, J. M. et Gómez-Álvarez, R. P. (2002). Calcul intégral (éd. Illustré). Madrid: Éditorial ESIC.
- Unican. Histoire du concept d'intégrale. Récupéré de: repositorio.unican.es
- UIS. Riemann fait les sommes. Récupéré de: matematicas.uis.edu.co
- Wikipédia. Somme de Riemann. Récupéré de: es.wikipedia.com
- Wikipédia. Intégration de Riemann. Récupéré de: es.wikipedia.com

Personne n'a encore commenté ce post.