
Théorie des ensembles caractéristiques, éléments, exemples, exercices
La théorie des ensembles C'est une branche de la logique-mathématiques qui se charge de l'étude des relations entre entités appelées ensembles. Les ensembles se caractérisent par être des collections d'objets de même nature. Ces objets sont les éléments de l'ensemble et peuvent être: des chiffres, des lettres, des figures géométriques, des mots qui représentent des objets, les objets eux-mêmes et d'autres.
C'est Georg Cantor, vers la fin du XIXe siècle, qui propose la théorie des ensembles. Alors que d'autres mathématiciens notables du XXe siècle ont fait leur formalisation: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel entre autres..

Les diagrammes de Venn sont la manière graphique de représenter un ensemble, et il se compose d'une figure plane fermée à l'intérieur de laquelle se trouvent les éléments de l'ensemble.
Par exemple, dans la figure 1, deux ensembles A et B sont représentés, qui ont des éléments en commun, les éléments communs à A et B.Ils forment un nouvel ensemble appelé ensemble d'intersection de A et B, qui s'écrit sous la forme symbolique comme suit:
A ∩ B
Index des articles
- 1 Fonctionnalités
- 2 types d'ensembles
- 2.1 Ensemble fini
- 2.2 Ensemble infini
- 2.3 Ensemble vide
- 2.4 Ensemble unitaire
- 2.5 Ensemble binaire
- 2.6 Ensemble universel
- 3 éléments de base
- 3.1 - Relations entre ensembles
- 3.2 - Propriétés d'inclusion
- 3.3 - Opérations entre ensembles
- 4 exemples
- 4.1 Exemple 1
- 4.2 Exemple 2
- 4.3 Exemple 3
- 4.4 Exemple 4
- 4.5 Exemple 5
- 5 exercices résolus
- 5.1 Exercice 1
- 5.2 Exercice 2
- 5.3 Exercice 3
- 5.4 Exercice 4
- 6 Références
Caractéristiques
L'ensemble est un concept primitif car il est en géométrie le concept de point, de ligne ou de plan. Il n'y a pas de meilleure façon d'exprimer le concept qu'en donnant des exemples:
Ensemble E formé par les couleurs du drapeau de l'Espagne. Cette manière d'exprimer l'ensemble est appelée par compréhension. Le même ensemble E écrit par extension est:
E = rouge, jaune
Dans ce cas, le rouge et le jaune sont des éléments de l'ensemble E. Il est à noter que les éléments sont listés entre accolades et ne sont pas répétés. Dans le cas du drapeau espagnol, il y a trois bandes colorées (rouge, jaune, rouge), dont deux sont répétées, mais les éléments ne sont pas répétés lorsque l'ensemble est exprimé..
Supposons l'ensemble V formé par les trois premières lettres de voyelle:
V = a, e, i
L'ensemble de puissance de V, noté P (V) est l'ensemble de tous les ensembles qui peuvent être formés avec les éléments de V:
P (V) = a, e, i, a, e, a, i, e, i, a, e, i
Types d'ensembles
Ensemble fini
C'est un ensemble dans lequel ses éléments sont dénombrables. Des exemples d'ensembles finis sont les lettres de l'alphabet espagnol, les voyelles de l'espagnol, les planètes du système solaire, entre autres. Le nombre d'éléments d'un ensemble fini s'appelle sa cardinalité.
Ensemble infini
Un ensemble infini est tout ce que le nombre de ses éléments est indénombrable, car quelle que soit la taille du nombre de ses éléments, il est toujours possible de trouver plus d'éléments.
Un exemple d'ensemble infini est l'ensemble des nombres naturels N, qui sous forme extensive s'exprime comme suit:
N = 1, 2, 3, 4, 5,…. Est clairement un ensemble infini, car quelle que soit la taille d'un entier naturel, le plus grand suivant peut toujours être trouvé, dans un processus sans fin. Clairement, la cardinalité d'un ensemble infini est ∞.
Ensemble vide
C'est l'ensemble qui ne contient aucun élément. L'ensemble vide V est noté Ø ou par une paire de clés sans éléments à l'intérieur:
V = = Ø.
L'ensemble vide est unique, il doit donc être incorrect de dire «un ensemble vide», la forme correcte est de dire «l'ensemble vide».
Parmi les propriétés de l'ensemble vide, nous avons qu'il s'agit d'un sous-ensemble de n'importe quel ensemble:
Ø ⊂ A
De plus, si un ensemble est un sous-ensemble de l'ensemble vide, alors nécessairement ledit ensemble sera le vide:
A ⊂ Ø ⇔ A = Ø
Ensemble unitaire
Un ensemble d'unités est un ensemble contenant un seul élément. Par exemple, l'ensemble des satellites naturels de la Terre est un ensemble unitaire, dont le seul élément est la Lune. L'ensemble B d'entiers inférieurs à 2 et supérieurs à zéro n'a que l'élément 1, il s'agit donc d'un ensemble unitaire.
Ensemble binaire
Un ensemble est binaire s'il ne comporte que deux éléments. Par exemple l'ensemble X, tel que x est une solution en nombre réel de x ^ 2 = 2. Cet ensemble par extension s'écrit comme ceci:
X = -√2, + √2
Ensemble universel
L'ensemble universel est un ensemble qui contient d'autres ensembles du même type ou de la même nature. Par exemple, l'ensemble universel des nombres naturels est l'ensemble des nombres réels. Mais les nombres réels sont un ensemble universel aussi des entiers et des nombres rationnels.
Éléments essentiels
- Relations entre ensembles
Dans les assemblages, différents types de relations peuvent être établis entre eux et leurs éléments. Si deux ensembles A et B ont exactement les mêmes éléments entre eux, une relation d'égalité est établie, notée comme suit:
À = B
Si tous les éléments d'un ensemble A appartiennent à un ensemble B, mais que tous les éléments de B n'appartiennent pas à A, alors entre ces ensembles il y a une relation d'inclusion qui est notée comme ceci:
A ⊂ B, mais B ⊄ A
L'expression ci-dessus se lit comme suit: A est un sous-ensemble de B, mais B n'est pas un sous-ensemble de A.
Pour indiquer que certains ou certains éléments appartiennent à un ensemble, le symbole d'appartenance ∈ est utilisé, par exemple pour dire que x élément ou éléments appartiennent à l'ensemble A s'écrit symboliquement comme ceci:
x ∈ A
Si un élément n'appartient pas à l'ensemble A, cette relation s'écrit comme ceci:
et ∉ A
La relation d'appartenance se produit entre les éléments d'un ensemble et l'ensemble, à la seule exception de l'ensemble de puissance, l'ensemble de puissance étant la collection ou l'ensemble de tous les ensembles possibles qui peuvent être formés avec les éléments dudit ensemble..
Supposons que V = a, e, i, son ensemble de puissance est P (V) = a, e, i, a, e, a, i, e, i , a, e, i, dans ce cas l'ensemble V devient un élément de l'ensemble P (V) et s'écrit:
V ∈ P (V)
- Propriétés d'inclusion
La première propriété d'inclusion établit que chaque ensemble est contenu en lui-même, ou en d'autres termes, qu'il est un sous-ensemble de lui-même:
A ⊂ A
L'autre propriété de l'inclusion est la transitivité: si A est un sous-ensemble de B et B à son tour est un sous-ensemble de C, alors A est un sous-ensemble de C.Sous forme symbolique, la relation de transitivité s'écrit comme suit:
(A ⊂ B) ^ (B ⊂ C) => A ⊂ C
Voici le diagramme de Venn correspondant à la transitivité de l'inclusion:
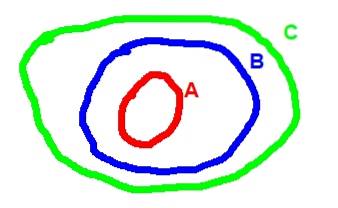
- Opérations entre les ensembles
Intersection
L'intersection est une opération entre deux ensembles qui donne naissance à un nouvel ensemble appartenant au même ensemble universel que les deux premiers. En ce sens, c'est une opération fermée.
Symboliquement, l'opération d'intersection est formulée comme ceci:
A⋂B = x / x∈A ^ x∈B
Un exemple est le suivant: l'ensemble A des lettres du mot «éléments» et l'ensemble B des lettres du mot «répété», l'intersection entre A et B s'écrit ainsi:
A⋂B = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s. L'ensemble universel U de A, de B et aussi de A⋂B est l'ensemble des lettres de l'alphabet espagnol.
syndicat
L'union de deux ensembles est l'ensemble formé par les éléments communs aux deux ensembles et les éléments non communs des deux ensembles. L'opération d'union entre les ensembles est exprimée symboliquement comme ceci:
A∪B = x / x∈A v x∈B
Différence
L'opération de différence de l'ensemble A moins l'ensemble B est désignée par A-B. A-B est un nouvel ensemble formé par tous les éléments qui sont dans A et qui n'appartiennent pas à B. Symboliquement, il s'écrit comme ceci:
A - B = x / x ∈ A ^ x ∉ B
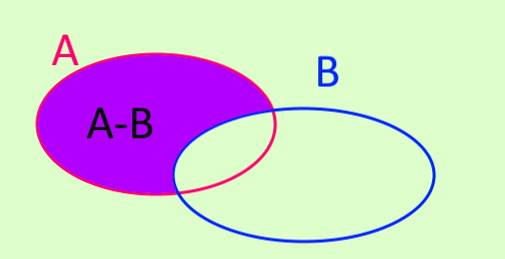
Différence symétrique
La différence symétrique est une opération entre deux ensembles où l'ensemble résultant est constitué des éléments non communs aux deux ensembles. La différence symétrique est symboliquement représentée comme ceci:
A⊕B = x / x∈ (A-B) ^ x∈ (B-A)
Exemples
Exemple 1
Le diagramme de Venn est une manière graphique de représenter des ensembles. Par exemple, l'ensemble C des lettres dans l'ensemble de mots est représenté comme ceci:

Exemple 2
Il est montré ci-dessous par les diagrammes de Venn que l'ensemble des voyelles dans le mot «ensemble» est un sous-ensemble de l'ensemble des lettres dans le mot «ensemble».

Exemple 3
Ensemble Ñ des lettres de l'alphabet espagnol est un ensemble fini, cet ensemble par extension s'écrit comme ceci:
Ñ = a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z et sa cardinalité est 27.
Exemple 4
Ensemble V des voyelles en espagnol est un sous-ensemble de l'ensemble Ñ:
V ⊂ Ñ c'est donc un ensemble fini.
L'ensemble fini V sous une forme extensive, il est écrit comme ceci: V = a, e, i, o, u et sa cardinalité est 5.
Exemple 5
Étant donné les ensembles A = 2, 4, 6, 8 et B = 1, 2, 4, 7, 9 déterminent A-B et B-A.
A - B sont les éléments de A qui ne sont pas dans B:
A - B = 6, 8
B - A sont les éléments de B qui ne sont pas dans A:
B - A = 1, 7, 9
Exercices résolus
Exercice 1
Ecrire sous forme symbolique et aussi par extension l'ensemble P des entiers naturels pairs inférieurs à 10.
Solution: P = x∈ N / x < 10 ^ x mod 2 = 0
P = 2, 4, 6, 8
Exercice 2
Supposons l'ensemble A formé par les nombres naturels qui sont des facteurs de 210, et l'ensemble B formé par les nombres naturels premiers inférieurs à 9. Déterminer par extension les deux ensembles et établir la relation entre les deux ensembles.
Solution: Pour déterminer les éléments de l'ensemble A, il faut commencer par trouver les facteurs du nombre naturel 210:
210 = 2 * 3 * 5 * 7
Alors l'ensemble A s'écrit:
A = 2, 3, 5, 7
Nous considérons maintenant l'ensemble B, qui est les nombres premiers inférieurs à 9. 1 n'est pas premier car il ne répond pas à la définition de premier: "un nombre est premier si et seulement s'il a exactement deux diviseurs, 1 et le nombre lui-même" . Le 2 est pair et en même temps il est premier car il répond à la définition d'un premier, les autres nombres premiers inférieurs à 9 sont 3, 5 et 7. Ainsi l'ensemble B est:
B = 2, 3, 5, 7
Par conséquent, les deux ensembles sont égaux: A = B.
Exercice 3
Déterminer l'ensemble dont les éléments x sont différents de x.
Solution: C = x / x ≠ x
Puisque chaque élément, nombre ou objet est égal à lui-même, l'ensemble C ne peut pas être autre que l'ensemble vide:
C = Ø
Exercice 4
Soit l'ensemble des N de nombres naturels et Z l'ensemble des entiers. Déterminer N ⋂ Z et N ∪ Z.
Solution:
N ⋂ Z = x ∈ Z / x ≤ 0 = (-∞, 0]
N ∪ Z = Z car N ⊂ Z.
Les références
- Garo, M. (2014). Mathématiques: équations quadratiques: comment résoudre une équation quadratique. Marilù Garo.
- Haeussler, E. F. et Paul, R. S. (2003). Mathématiques pour la gestion et l'économie. Éducation Pearson.
- Jiménez, J., Rodríguez, M., Estrada, R. (2005). Mathématiques 1 SEP. Au seuil.
- Preciado, C. T. (2005). Cours de mathématiques 3e. Progreso éditorial.
- Mathématiques 10 (2018). "Exemples d'ensembles finis". Récupéré de: matematicas10.net
- Wikipédia. Théorie des ensembles. Récupéré de: es.wikipedia.com



Personne n'a encore commenté ce post.