
Explication du théorème de Bayes, applications, exercices
le Théorème de Bayes est une procédure qui permet d'exprimer la probabilité conditionnelle d'un événement aléatoire A donné B, en termes de distribution de probabilité de l'événement B étant donné A et la distribution de probabilité de seulement A.
Ce théorème est très utile, car grâce à lui nous pouvons relier la probabilité qu'un événement A se produise sachant que B s'est produit, avec la probabilité que le contraire se produise, c'est-à-dire que B se produise étant donné A.
Le théorème de Bayes était une proposition d'argent du révérend Thomas Bayes, un théologien anglais du XVIIIe siècle qui était également mathématicien. Il était l'auteur de plusieurs ouvrages en théologie, mais à l'heure actuelle, il est connu pour quelques traités mathématiques, parmi lesquels le théorème de Bayes déjà mentionné se distingue comme le résultat principal..
Bayes a traité de ce théorème dans un ouvrage intitulé "Un essai pour résoudre un problème dans la doctrine du hasard", publié en 1763, et sur lequel un grand nombre ont été développés..
Index des articles
- 1 Explication
- 2 Applications du théorème de Bayes
- 2.1 Exercices résolus
- 3 Références
Explication
Premièrement, pour une meilleure compréhension de ce théorème, certaines notions de base de la théorie des probabilités sont nécessaires, en particulier le théorème de multiplication de la probabilité conditionnelle, qui stipule que
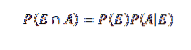
Pour E et A événements arbitraires d'un espace échantillon S.
Et la définition des partitions, qui nous dit que si nous avons A1 ,Àdeux,… , Àn événements d'un espace échantillon S, ceux-ci formeront une partition de S, si le Aje sont mutuellement exclusifs et leur union est S.
Compte tenu de cela, soit B un autre événement. Nous pouvons donc voir B comme
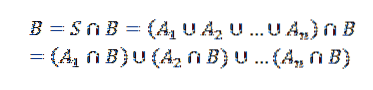
Où le Aje intersectés avec B sont des événements mutuellement exclusifs.
Et par conséquent,
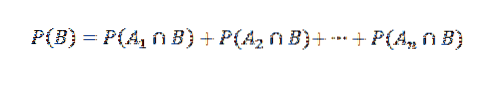
Ensuite, en appliquant le théorème de multiplication
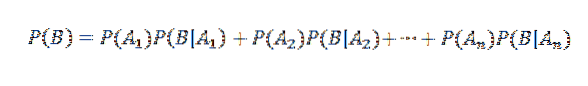
En revanche, la probabilité conditionnelle de Ai étant donné B est définie par
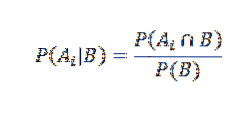
En remplaçant de manière appropriée, nous avons cela pour tout i
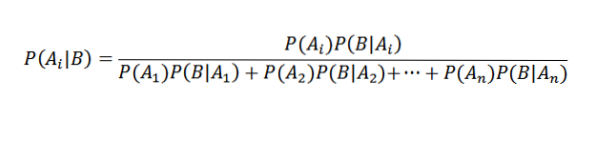
Applications du théorème de Bayes
Grâce à ce résultat, des groupes de recherche et diverses entreprises ont réussi à améliorer des systèmes basés sur la connaissance..
Par exemple, dans l'étude des maladies, le théorème de Bayes peut aider à discerner la probabilité qu'une maladie se trouve dans un groupe de personnes ayant une caractéristique donnée, en prenant comme données les taux globaux de la maladie et la prédominance de ces caractéristiques dans les deux cas. personnes en bonne santé et malades.
En revanche, dans le monde des hautes technologies, il a influencé de grandes entreprises qui ont développé, grâce à ce résultat, des logiciels "Knowledge-Based".
Comme exemple quotidien, nous avons l'assistant Microsoft Office. Le théorème de Bayes aide le logiciel à évaluer les problèmes que présente l'utilisateur et à déterminer les conseils à fournir et ainsi être en mesure d'offrir un meilleur service en fonction des habitudes de l'utilisateur..
Il convient de noter que cette formule a été ignorée jusqu'à une époque récente, c'est principalement parce que lorsque ce résultat a été développé il y a 200 ans, il y avait peu d'utilité pratique pour eux. Cependant, à notre époque, grâce à de grandes avancées technologiques, les scientifiques ont trouvé des moyens de mettre ce résultat en pratique.
Exercices résolus
Exercice 1
Une entreprise de téléphonie mobile dispose de deux machines A et B. 54% des téléphones portables produits sont fabriqués par la machine A et le reste par la machine B. Tous les téléphones portables produits ne sont pas en bon état.
La proportion de téléphones portables défectueux fabriqués par A est de 0,2 et par B est de 0,5. Quelle est la probabilité qu'un téléphone portable de cette usine soit défectueux? Quelle est la probabilité que, sachant qu'un téléphone portable est défectueux, il provienne de la machine A?
Solution
Ici, vous avez une expérience qui se déroule en deux parties; dans la première partie, les événements se produisent:
A: cellule fabriquée par la machine A.
B: cellule fabriquée par la machine B.
Puisque la machine A produit 54% des téléphones portables et que le reste est produit par la machine B, il s'ensuit que la machine B produit 46% des téléphones portables. Les probabilités de ces événements sont données, à savoir:
P (A) = 0,54.
P (B) = 0,46.
Les événements de la deuxième partie de l'expérience sont:
D: téléphone portable défectueux.
E: téléphone portable non défectueux.
Comme indiqué dans l'énoncé, les probabilités de ces événements dépendent du résultat obtenu dans la première partie:
P (D | A) = 0,2.
P (D | B) = 0,5.
En utilisant ces valeurs, les probabilités des compléments de ces événements peuvent également être déterminées, c'est-à-dire:
P (E | A) = 1 - P (D | A)
= 1 - 0,2
= 0,8
Oui
p (E | B) = 1 - P (D | B)
= 1 - 0,5
= 0,5.
Maintenant, l'événement D peut être écrit comme suit:
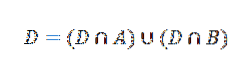
Utilisation du théorème de multiplication pour les résultats de probabilité conditionnelle:
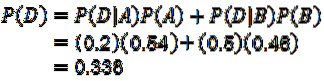
Avec lequel on répond à la première question.
Il ne nous reste plus qu'à calculer P (A | D), pour lequel le théorème de Bayes est appliqué:
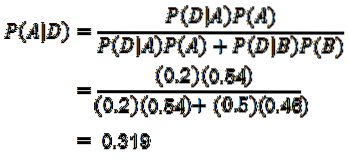
Grâce au théorème de Bayes, on peut affirmer que la probabilité qu'un téléphone portable ait été fabriqué par la machine A, sachant que le téléphone portable est défectueux, est de 0,319.
Exercice 2
Trois boîtes contiennent des boules noires et blanches. La composition de chacun d'eux est la suivante: U1 = 3B, 1N, U2 = 2B, 2N, U3 = 1B, 3N.
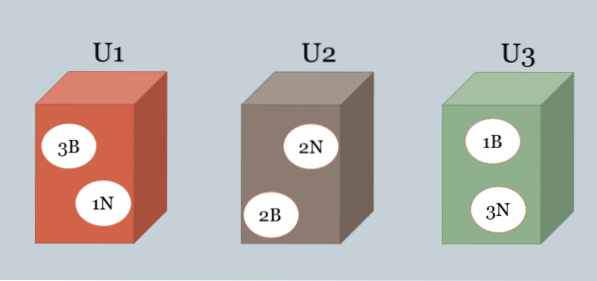
L'une des cases est choisie au hasard et une balle est tirée au hasard qui s'avère être blanche. Quelle est la boîte la plus susceptible d'avoir été choisie?
Solution
En utilisant U1, U2 et U3, nous représenterons également la boîte choisie.
Ces événements constituent une partition de S et on vérifie que P (U1) = P (U2) = P (U3) = 1/3 puisque le choix de la boîte est aléatoire.
Si B = la boule tirée est blanche, on aura P (B | U1) = 3/4, P (B | U2) = 2/4, P (B | U3) = 1/4 .
Ce que nous voulons obtenir est la probabilité que la balle ait été sortie de la boîte Ui sachant que ladite balle était blanche, c'est-à-dire P (Ui | B), et voir laquelle des trois valeurs était la plus élevée à connaître de quelle boîte a probablement été l'extraction de la boule blanche.
Application du théorème de Bayes à la première des cases:
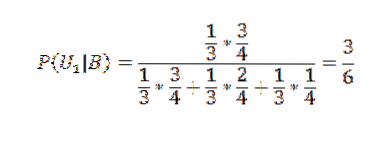
Et pour les deux autres:
P (U2 | B) = 2/6 et P (U3 | B) = 1/6.
Ensuite, la première des cases est celle qui a la plus forte probabilité d'avoir été choisie pour l'extraction de la boule blanche..
Les références
- Kai Lai Chung. Théorie élémentaire de la rentabilité avec des processus stochastiques. Springer-Verlag New York Inc
- Kenneth.H. Rosen: Mathématiques discrètes et ses applications. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Probabilité et applications statistiques. S.A. ALHAMBRA MEXICAIN.
- Seymour Lipschutz Ph.D. 2000 Problèmes résolus de mathématiques discrètes. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Problèmes de théorie et de probabilité. McGRAW-HILL.



Personne n'a encore commenté ce post.