le Théorème d'existence et d'unicité établit les conditions nécessaires et suffisantes pour qu'une équation différentielle du premier ordre, avec une condition initiale donnée, ait une solution et que cette solution soit aussi la seule.
Cependant, le théorème ne donne aucune technique ni aucune indication sur la manière de trouver une telle solution. Le théorème d'existence et d'unicité est également étendu aux équations différentielles d'ordre supérieur avec des conditions initiales, ce que l'on appelle le problème de Cauchy..
L'énoncé formel du théorème d'existence et d'unicité est le suivant:
"Pour une équation différentielle y '(x) = f (x, y) avec condition initiale y (a) = b, Ça existe au moins une solution dans une région rectangulaire du plan XY contenant au point (un B), Oui f (x, y) il est continu dans cette région. Et si la dérivée partielle de F à l'égard de Y: g = ∂f / ∂et est continue dans cette même région rectangulaire, alors la solution est unique dans un voisinage du point (un B) contenu dans la région de continuité de F Oui g."
L'utilité de ce théorème réside d'abord dans le fait de savoir quelles sont les régions du plan XY dans lesquelles une solution peut exister et aussi, de savoir si la solution trouvée est la seule possible ou s'il y en a d'autres..
Notez que dans le cas où la condition d'unicité n'est pas satisfaite, le théorème ne peut pas prédire combien de solutions au total a le problème de Cauchy: peut-être est-ce une, deux ou plus.
Index des articles
Pour ce théorème, deux preuves possibles sont connues, l'une d'elles est la preuve de Charles Émile Picard (1856-1941) et l'autre est due à Giuseppe Peano (1858-1932) d'après les travaux d'Augustin Louis Cauchy (1789-1857) ).
Il est à noter que les esprits mathématiques les plus brillants du XIXe siècle ont participé à la preuve de ce théorème, de sorte que l'on peut deviner qu'aucun des deux n'est simple..
Pour prouver formellement le théorème, il faut d'abord établir une série de concepts mathématiques plus avancés, tels que les fonctions de type Lipschitz, les espaces de Banach, le théorème d'existence de Carathéodory, et plusieurs autres, qui sortent du cadre de l'article..
Une grande partie des équations différentielles manipulées en physique traitent des fonctions continues dans les régions d'intérêt, nous nous limiterons donc à montrer comment le théorème est appliqué dans des équations simples.
Considérons l'équation différentielle suivante avec une condition initiale:
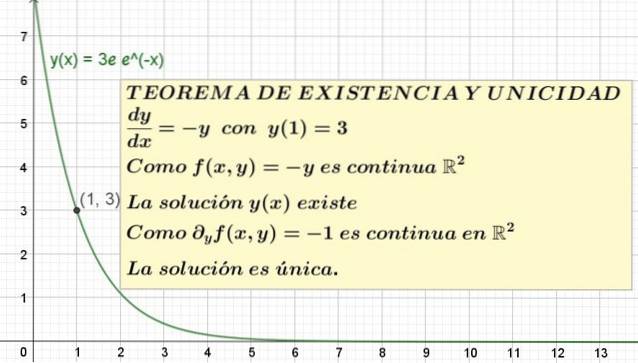
y '(x) = - y; avec y (1) = 3
Y a-t-il une solution à ce problème? Est-ce la seule solution possible?
En premier lieu, l'existence de la solution de l'équation différentielle est évaluée et qu'elle remplit également la condition initiale.
Dans cet exemple f (x, y) = - y la condition d'existence exige de savoir si f (x, y) est continue dans une région du plan XY qui contient le point de coordonnées x = 1, y = 3.
Mais f (x, y) = - y est le fonction affine, qui est continue dans le domaine des nombres réels et existe dans toute la gamme des nombres réels.
On en conclut donc que f (x, y) est continue dans Rdeux, donc le théorème garantit l'existence d'au moins une solution.
Sachant cela, il faut évaluer si la solution est unique ou si, au contraire, il y en a plusieurs. Pour cela, il est nécessaire de calculer la dérivée partielle de F par rapport à la variable Oui:
∂f / ∂y = ∂ (-y) / ∂y = -1
Ensuite g (x, y) = -1 qui est une fonction constante, qui est également définie pour tout Rdeux et il y est aussi continu. Il s'ensuit que le théorème d'existence et d'unicité garantit que ce problème de valeur initiale a une solution unique, bien qu'il ne nous dise pas ce que c'est..
Considérons l'équation différentielle ordinaire du premier ordre suivante avec la condition initiale:
y '(x) = 2√y; y (0) = 0.
Y a-t-il une solution y (x) pour ce problème? Si tel est le cas, déterminez s'il y en a un ou plusieurs.
Nous considérons la fonction f (x, y) = 2√y. La fonction F est défini uniquement pour y≥0, puisque nous savons qu'un nombre négatif n'a pas de racine réelle. En outre f (x, y) est continue dans le demi-plan supérieur de Rdeux y compris l'axe X, donc le théorème d'existence et d'unicité garantit au moins une solution dans cette région.
Maintenant, la condition initiale x = 0, y = 0 est sur le bord de la région de solution. Ensuite, nous prenons la dérivée partielle de f (x, y) par rapport à y:
∂f/ ∂y = 1 / √y
Dans ce cas, la fonction n'est pas définie pour y = 0, précisément là où la condition initiale est.
Que nous dit le théorème? Il nous dit que bien que nous sachions qu'il existe au moins une solution, le demi-plan supérieur de l'axe X incluant l'axe X, puisque la condition d'unicité n'est pas remplie, il n'y a aucune garantie qu'il y aura une solution unique.
Cela signifie qu'il pourrait y avoir une ou plusieurs solutions dans la région de continuité de f (x, y). Et comme toujours, le théorème ne nous dit pas ce qu'ils pourraient être.
Résolvez le problème de Cauchy dans l'exemple 1:
y '(x) = - y; avec y (1) = 3.
Trouvez la fonction y (x) qui satisfait l'équation différentielle et la condition initiale.
Dans l'exemple 1, il a été déterminé que ce problème a une solution et est également unique. Pour trouver la solution, la première chose à noter est qu'il s'agit d'une équation différentielle du premier degré de variables séparables, qui s'écrit comme suit:
dy / dx = - y → dy = -y dx
Diviser entre et dans les deux membres pour séparer les variables que nous avons:
dy / y = - dx
L'intégrale indéfinie est appliquée dans les deux membres:
∫ (1 / an) dy = - ∫dx
Résoudre les intégrales indéfinies que nous avons:
ln (y) = -x + C
où C est une constante d'intégration déterminée par la condition initiale:
ln (3) = -1 + C, c'est-à-dire C = 1 + ln (3)
Remplacer la valeur de C et la réorganiser reste:
ln (y) - ln (3) = -x + 1
Application de la propriété suivante des logarithmes:
La différence des logarithmes est le logarithme du quotient
L'expression ci-dessus peut être réécrite comme ceci:
ln (y / 3) = 1 - x
La fonction exponentielle avec base e dans les deux membres est appliquée pour obtenir:
y / 3 = e(1 fois)
Ce qui équivaut à:
y = 3e e-X
C'est la solution unique de l'équation y '= -y avec y (1) = 3. Le graphique de cette solution est montré dans la figure 1.
Trouvez deux solutions au problème posé dans l'exemple 2:
y '(x) = 2√ (y); y (0) = 0.
C'est aussi une équation de variables séparables, qui, écrite sous forme différentielle, ressemble à ceci:
dy / √ (y) = 2 dx
Prendre l'intégrale indéfinie dans les deux membres reste:
deux √ (y) = 2 x + C
Comment sais-tu ça y≥0 dans la région de solution, nous avons:
y = (x + C)deux
Mais puisque la condition initiale x = 0, y = 0 doit être remplie, alors la constante C est nulle et la solution suivante reste:
y (x) = xdeux.
Mais cette solution n'est pas unique, la fonction y (x) = 0 est aussi une solution au problème posé. Le théorème d'existence et d'unicité appliqué à ce problème dans l'exemple 2 avait déjà prédit qu'il pourrait y avoir plus d'une solution.
Personne n'a encore commenté ce post.