
Caractéristiques de tir horizontal, formules et équations, exercices
le tir horizontal C'est le lancement d'un projectile à vitesse horizontale à partir d'une certaine hauteur et laissé à l'action de la gravité. Sans tenir compte de la résistance de l'air, la trajectoire décrite par le mobile aura la forme d'un arc de parabole.
La projection d'objets horizontalement est assez courante. Les projectiles sont lancés à toutes sortes de fins: des pierres avec lesquelles les barrages ont été frappés au début de l'histoire, à celles menées dans les sports de balle et sont suivies de près par la foule..
Index des articles
- 1 Fonctionnalités
- 2 Formules et équations
- 2.1 Position, vitesse, temps de vol et plage horizontale maximale
- 3 exercices résolus
- 3.1 -Exercice résolu 1
- 3.2 -Exercice résolu 2
- 4 Références
Caractéristiques
Les principales caractéristiques du plan horizontal sont:
-La vitesse initiale donnée au projectile est perpendiculaire à la gravité.
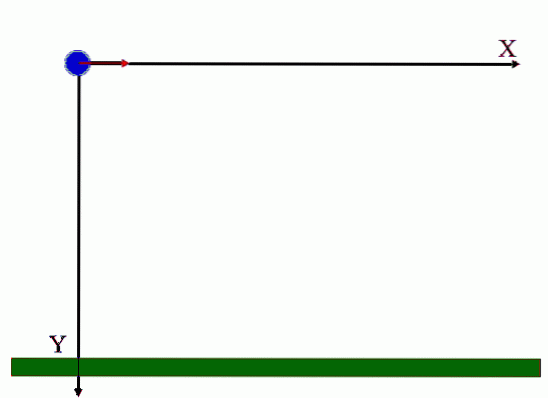
-Le mouvement a lieu dans un plan, il prend donc deux coordonnées: X Oui Oui.
-Il se fait à partir d'une certaine hauteur H au-dessus du sol.
-Le temps que dure le projectile dans l'air s'appelle temps de vol.
-Des facteurs tels que la résistance de l'air et les fluctuations de la valeur de g.
-La forme, la taille et la masse du projectile n'influencent pas son mouvement.
-Le mouvement se décompose en deux mouvements simultanés: l'un vertical vers le bas sous l'action de g; l'autre, horizontal, à vitesse constante.
Formules et équations
Les équations cinématiques pour le lancement horizontal sont obtenues à partir des équations de la chute libre et de celles du mouvement rectiligne uniforme..
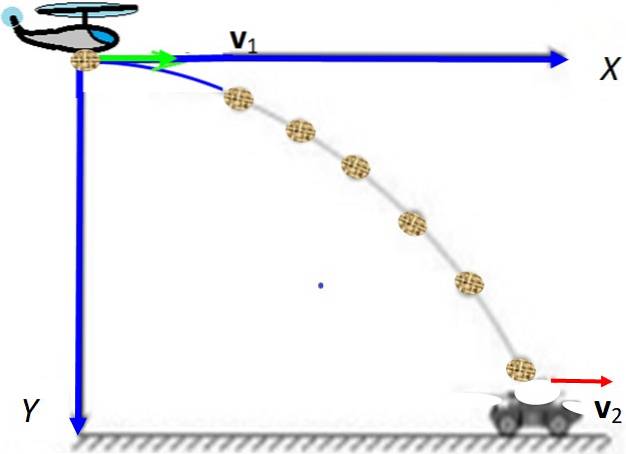
Comme le montre clairement l'animation de la figure 1, le projectile reçoit une vitesse initiale horizontale, notée vou alors = vbœuf je (le caractère gras dans le texte imprimé indique qu'il s'agit d'un vecteur).
Notez que la vitesse initiale a une magnitude vbœuf et est dirigé le long de l'axe X, quelle est la direction du vecteur unitaire je. L'animation montre également que la vitesse initiale n'a pas de composante verticale, mais à mesure qu'elle tombe, cette composante augmente uniformément, grâce à l'action de g, accélération gravitationnelle.
Quant à la composante horizontale de la vitesse, elle reste constante pendant toute la durée du mouvement.
Selon ce qui précède, les positions sont établies en fonction du temps, à la fois sur l'axe horizontal et sur l'axe vertical. La direction vers la droite est considérée comme l'axe + x, tandis que la direction vers le bas est la direction -y. La valeur de la gravité est g = -9,8 m / sdeux ou alors -32 pi / sdeux:
x (t) = xou alors + vbœuf.t (position horizontale); vbœuf c'est constant
y (t) = you alors + vHey.t - ½ g.tdeux (position verticale); vOui = vHey - g.t (vitesse verticale)
Position, vitesse, temps de vol et plage horizontale maximale
Les équations sont simplifiées en choisissant les positions de départ suivantes: Xou alors = 0, Ouiou alors = 0 sur le site de lancement. En outre vHey = 0, puisque le mobile est projeté horizontalement. Avec ce choix, les équations du mouvement sont comme ceci:
x (t) = vbœuf.t; vX = vbœuf
y (t) = - ½ g.tdeux; vOui = - g.t
Lorsque le temps n'est pas disponible, l'équation reliant les vitesses et les déplacements est utile. Ceci est valable pour la vitesse verticale, puisque l'horizontale reste constante tout au long du mouvement:
vOuideux = vHeydeux + 2.g .y = 2.g.y
Temps de vol
Pour calculer le temps de vol tvol, supposons que le mobile soit projeté d'une hauteur H sur le plancher. Comme l'origine du système de référence a été choisie au point de lancement, lorsqu'il atteint le sol, il est dans la position -H. En remplaçant cela dans l'équation 2), nous obtenons:
-H = - ½ g.tdeuxvol
tvol = (2H / g)½
Portée maximale
le portée horizontale s'obtient en remplaçant cette fois par x (t):
Xmax = vbœuf. (2H / g)½
Exercices résolus
-Exercice résolu 1
Un hélicoptère vole horizontalement, maintenant une élévation constante de 580 m lorsqu'il laisse tomber une boîte contenant de la nourriture au-dessus d'un camp de réfugiés. La boîte atterrit à une distance horizontale de 150 m du point de son lancement. Trouvez: a) Le temps de vol de la boîte.
b) La vitesse de l'hélicoptère.
c) À quelle vitesse la boîte a-t-elle touché le sol??
Solution
a) La hauteur H à partir de laquelle la nourriture tombe est H = 500 m. Avec ces données, lors de la substitution, nous obtenons:
tvol = (2H / g)½= (2 x 580 / 9,8) ½s = 10,9 s
b) L'hélicoptère porte la vitesse horizontale initiale vbœuf du package et comme l'une des données est Xmax:
Xmax = vbœuf. (2H / g)½ ® vbœuf = xmax / (2H / g)½= xmax / tvol = 150 m / 10,9 s = 13,8 m / s
c) La vitesse du projectile à tout instant est:
vOui = -g.t = -9,8 m / sdeux x 10,9 s = -106,82 m / s = - 384,6 km / h
Le signe négatif indique que le mobile descend.
-Exercice résolu 2
D'un avion volant horizontalement à une hauteur H = 500 m Oui 200 km / h un colis tombe et doit tomber sur un véhicule ouvert qui se déplace à 18 km / h sur la route. Dans quelle position l'avion doit-il déposer le colis pour qu'il tombe dans le véhicule? Ne tenez pas compte de la résistance de l'air ou de la vitesse du vent.
Solution
Il est pratique de passer d'abord toutes les unités au système international:
18 km / h = 6 m / s
200 km / h = 55 m / s
Il existe deux mobiles: l'avion (1) et le véhicule (2) et il est nécessaire de choisir un système de coordonnées pour les localiser tous les deux. Il est pratique de le faire au point de départ du colis dans l'avion. Le colis est projeté horizontalement à la vitesse à laquelle l'avion transporte: v1, pendant que le véhicule se déplace à vdeux supposée constante.
-Avion
Position initiale: x = 0; y = 0
Vitesse initiale = v1 (horizontal)
Equations de position: y (t) = -½g.tdeux ; x (t) = v1.t
-Véhicule
Position initiale: x = 0, y = -H
Vitesse initiale = vdeux (constant)
x (t) = xou alors + vdeux. t
La durée du vol du forfait est:
tvol = (2H / g)½ = (2 × 500 / 9,8)½s = 10,1 s
Pendant ce temps, le colis a subi un déplacement horizontal de:
Xmax = vbœuf . (2H / g)½= 55 m / s x 10,1 s = 556 m.
Pendant ce temps, le véhicule s'est également déplacé horizontalement:
x (t) = v1.t = 6 m / s x10,1 s = 60,6 m
Si l'avion laisse tomber le colis immédiatement quand il voit le véhicule passer sous lui, il ne le fera pas tomber à l'intérieur. Pour que cela se produise, vous devez le jeter plus en arrière:
d = 556 m - 60,6 m = 495,4 m.
Les références
- Bauer, W. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill. 74-84.
- Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique. Édité par Douglas Figueroa (USB). 117-164.
- Mouvement d'un projectile. Récupéré de: phys.libretexts.org.
- Rex, A. 2011. Fondamentaux de la physique. Pearson. 53-58.
- Tippens, P. 2011. Physique: concepts et applications. 7e édition. McGraw Hill. 126-131.


Personne n'a encore commenté ce post.