
Caractéristiques du tir parabolique oblique, formules, équations, exemples
le tir parabolique oblique est un cas particulier de mouvement de chute libre dans lequel la vitesse initiale du projectile forme un certain angle avec l'horizontale, résultant en une trajectoire parabolique.
La chute libre est un cas de mouvement à accélération constante, dans lequel l'accélération est celle de la gravité, qui pointe toujours verticalement vers le bas et a une magnitude de 9,8 m / s ^ 2. Cela ne dépend pas de la masse du projectile, comme l'a montré Galileo Galilei en 1604.
Si la vitesse initiale du projectile est verticale, la chute libre a une trajectoire droite et verticale, mais si la vitesse initiale est oblique alors la trajectoire de chute libre est une courbe parabolique, un fait également démontré par Galileo.
Des exemples de mouvement parabolique sont la trajectoire d'une balle de baseball, la balle tirée d'un canon et le jet d'eau sortant d'un tuyau..
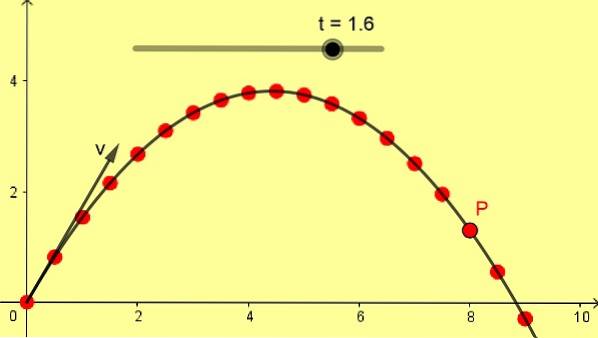
La figure 1 montre un tirant d'eau parabolique oblique de 10 m / s avec un angle de 60 °. L'échelle est en mètres et les positions successives de P sont prises avec un écart de 0,1 s à partir de l'instant initial 0 seconde.
Index des articles
- 1 Formules
- 1.1 Position et vitesse
- 2 équations
- 2.1 Équations paramétriques
- 2.2 Équation de la trajectoire
- 3 exemples
- 3.1 Exemple 1
- 3.2 Exemple 2
- 3.3 Exemple 3
- 4 Références
Formules
Le mouvement d'une particule est entièrement décrit si sa position, sa vitesse et son accélération sont connues en fonction du temps..
Le mouvement parabolique résultant d'un tir oblique est la superposition d'un mouvement horizontal à vitesse constante, plus un mouvement vertical à accélération constante égale à l'accélération de la pesanteur..
Les formules qui s'appliquent au tirant d'eau parabolique oblique sont celles qui correspondent à un mouvement à accélération constante a = g, notez que le gras a été utilisé pour indiquer que l'accélération est une quantité vectorielle.
Position et vitesse
Dans un mouvement à accélération constante, la position dépend mathématiquement du temps sous forme quadratique.
Si nous dénotons r(t) position à l'heure t, rou alors la position à l'instant initial, vou alors Vitesse initiale, g accélération et t = 0 comme instant initial la formule qui donne la position pour chaque instant de temps t c'est:
r(t) = rou alors + vou alors t + ½ g tdeux
Le gras dans l'expression ci-dessus indique qu'il s'agit d'une équation vectorielle.
La vitesse en fonction du temps est obtenue en prenant la dérivée par rapport à t de la position et le résultat est:
v(t) = vou alors + g t
Et pour obtenir l'accélération en fonction du temps, la dérivée de la vitesse par rapport à t donnant comme résultat:
à(t) = g
Lorsque le temps n'est pas disponible, il existe une relation entre la vitesse et la position, qui est donnée par:
vdeux = vou alorsdeux - 2 g (et - moi)
Équations
Ensuite, nous trouverons les équations qui s'appliquent à un tir parabolique oblique sous forme cartésienne.
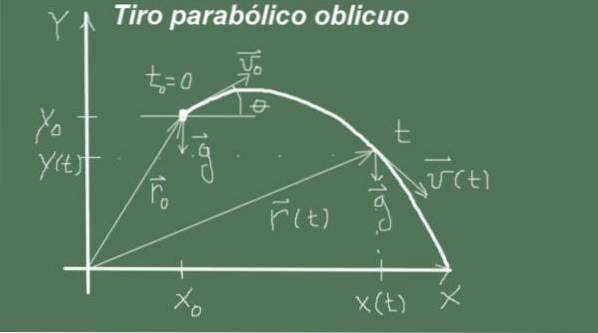
Le mouvement commence dans l'instant t = 0 avec position de départ (xo, moi) et vitesse de grandeur vou alors et angle θ, c'est-à-dire que le vecteur de vitesse initial est (vou alors cosθ, vou alors senθ). Le mouvement se poursuit avec une accélération
g = (0, -g).
Equations paramétriques
Si la formule vectorielle qui donne la position en fonction du temps est appliquée et que les composants sont groupés et égalisés, alors les équations qui donnent les coordonnées de la position à tout instant du temps t seront obtenues.
x (t) = xou alors + vbœuf t
y (t) = you alors + vHey t -½ g tdeux
De même, nous avons les équations pour les composantes de la vitesse en fonction du temps.
vX(t) = vbœuf
vOui(t) = vHey - g t
Où: vbœuf = vou alors cosθ; vHey = vou alors senθ
Équation de la trajectoire
y = A x ^ 2 + B x + C
A = -g / (2 vbœuf^ 2)
B = (vHey/ vbœuf + g xou alors/ vbœuf^ 2)
C = (etou alors - vHey Xou alors / vbœuf)
Exemples
Exemple 1
Répondre aux questions suivantes:
a) Pourquoi, dans les problèmes de tirant d'eau parabolique, l'effet du frottement avec l'air est-il généralement négligé??
b) La forme de l'objet a-t-elle une importance dans le tir parabolique?
Réponses
a) Pour que le mouvement d'un projectile soit parabolique, il est important que la force de frottement de l'air soit bien inférieure au poids de l'objet projeté.
Si une boule de liège ou un matériau léger est projeté, la force de friction est comparable au poids et sa trajectoire ne peut pas s'approcher d'une parabole.
Au contraire, s'il s'agit d'un objet lourd tel qu'une pierre, la force de frottement est négligeable par rapport au poids de la pierre et sa trajectoire se rapproche d'une parabole.
b) La forme de l'objet projeté est également pertinente. Si une feuille de papier est jetée en forme d'avion, son mouvement ne sera pas en chute libre ou parabolique, car la forme favorise la résistance de l'air.
En revanche, si la même feuille de papier est compactée en boule, le mouvement qui en résulte est très similaire à une parabole.
Exemple 2
Un projectile est lancé depuis le sol horizontal avec une vitesse de 10 m / s et un angle de 60 °. Ce sont les mêmes données avec lesquelles la figure 1 a été élaborée. Avec ces données, trouvez:
a) Moment où il atteint la hauteur maximale.
b) La hauteur maximale.
c) Vitesse à hauteur maximale.
d) Position et vitesse à 1,6 s.
e) Au moment où il touche à nouveau le sol.
f) La portée horizontale.
Solution à)
La vitesse verticale en fonction du temps est
vOui(t) = vHey - g t = vou alors sinθ - g t = 10 sin60º - 9,8 t = 8,66 - 9,8 t
Au moment où la hauteur maximale est atteinte, la vitesse verticale est nulle pendant un instant.
8,66 - 9,8 t = 0 ⇒ t = 0,88 s.
Solution b)
La hauteur maximale est donnée par la coordonnée Oui pour l'instant où cette hauteur est atteinte:
et (0,88s) = I + go t -½ g t ^deux = 0 + 8,66 * 0,88-½ 9,8 0,88 ^deux =
3,83 m
Par conséquent, la hauteur maximale est de 3,83 m.
Solution c)
La vitesse à hauteur maximale est horizontale:
vX(t) = vbœuf = vou alors cosθ = 10 cos60º = 5 m / s
Solution d)
La position à 1,6 s est:
x (1,6) = 5 * 1,6 = 8,0 m
et (1,6) = 8,66 * 1,6-½ 9,8 1,6deux = 1,31 m
Solution e)
Lorsque la coordonnée y touche le sol, alors:
y (t) = 8,66 * t-½ 9,8 tdeux = 0 ⇒ t = 1,77 s
Solution f)
La portée horizontale est la coordonnée x juste au moment où elle touche le sol:
x (1,77) = 5 * 1,77 = 8,85 m
Exemple 3
Trouvez l'équation de la trajectoire avec les données de l'exemple 2.
Solution
L'équation paramétrique du chemin est:
x (t) = 5 * t
y (t) = 8,66 * t-½ 9,8 t ^deux
Et l'équation cartésienne s'obtient en résolvant t à partir du premier et en substituant dans le second
y = 8,66 * (x / 5) -½ 9,8 (x / 5) ^deux
Simplifier:
y = 1,73 x - 0,20 x ^ 2
Les références
- P. P. Teodorescu (2007). "Cinématique". Systèmes mécaniques, modèles classiques: mécanique des particules. Springer.
- Resnick, Halliday et Krane (2002). Physique Volume 1. Cecsa, Mexique.
- Thomas Wallace Wright (1896). Éléments de mécanique, y compris la cinématique, la cinétique et la statique. E et FN Spon.
- Wikipédia. Mouvement parabolique. Récupéré de es.wikipedia.org.
- Wikipédia. Mouvement du projectile récupéré de en.wikipedia.org.

Personne n'a encore commenté ce post.