
Définition de la transformation de Laplace, histoire et à quoi ça sert
La transformation de Laplace Ces dernières années, il a été d'une grande importance dans les études d'ingénierie, de mathématiques et de physique, entre autres domaines scientifiques, car en plus d'être d'un grand intérêt théorique, il offre un moyen simple de résoudre des problèmes issus de la science et de l'ingénierie..
À l'origine, la transformée de Laplace a été présentée par Pierre-Simón Laplace dans son étude sur la théorie des probabilités et a été initialement traitée comme un objet mathématique d'intérêt purement théorique..

Les applications actuelles surviennent lorsque divers mathématiciens ont tenté de donner une justification formelle aux «règles opérationnelles» utilisées par Heaviside dans l'étude des équations de la théorie électromagnétique..
Index des articles
- 1 Définition
- 1.1 Exemples
- 1.2 Théorème (Conditions d'existence suffisantes)
- 1.3 Transformée de Laplace de certaines fonctions de base
- 2 Histoire
- 2.1 1782, Laplace
- 2.2 Oliver Heaviside
- 3 propriétés
- 3.1 Linéarité
- 3.2 Premier théorème de traduction
- 3.3 Deuxième théorème de traduction
- 3.4 Changement d'échelle
- 3.5 Transformée de Laplace des dérivés
- 3.6 Transformée de Laplace des intégrales
- 3.7 Multiplication par tn
- 3.8 Division par t
- 3.9 Fonctions périodiques
- 3.10 Comportement de F (s) lorsque s tend vers l'infini
- 4 Transformées inverses
- 4.1 Exercice
- 5 Applications de la transformée de Laplace
- 5.1 Équations différentielles
- 5.2 Systèmes d'équations différentielles
- 5.3 Mécanique et circuits électriques
- 6 Références
Définition
Soit f une fonction définie pour t ≥ 0. La transformée de Laplace est définie comme suit:
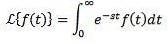
On dit que la transformée de Laplace existe si l'intégrale précédente converge, sinon on dit que la transformée de Laplace n'existe pas.
En général, les lettres minuscules sont utilisées pour désigner la fonction à transformer, et la lettre majuscule correspond à sa transformation. De cette façon, nous aurons:
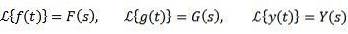
Exemples
Considérons la fonction constante f (t) = 1. Nous avons que sa transformée est:
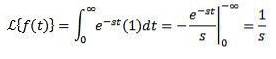
Chaque fois que l'intégrale converge, c'est-à-dire chaque fois que s> 0. Sinon, s < 0, la integral diverge.
Soit g (t) = t. Sa transformée de Laplace est donnée par
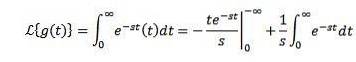
En intégrant par pièces et en sachant que vous-st tend vers 0 lorsque t tend vers l'infini et s> 0, avec l'exemple précédent, nous avons:
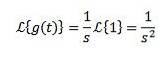
La transformée peut exister ou non, par exemple pour la fonction f (t) = 1 / t l'intégrale qui définit sa transformée de Laplace ne converge pas et donc sa transformée n'existe pas.
Les conditions suffisantes pour garantir que la transformée de Laplace d'une fonction f existe sont que f est continue en parties pour t ≥ 0 et est d'ordre exponentiel.
Une fonction est dite continue par morceaux pour t ≥ 0, lorsque pour tout intervalle [a, b] avec a> 0, il existe un nombre fini de points tk, où f a des discontinuités et est continue dans chaque sous-intervalle [tk-1,tk].
Par contre, on dit qu'une fonction est d'ordre exponentiel c s'il existe des constantes réelles M> 0, c et T> 0 telles que:
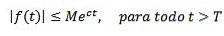
Comme exemples, nous avons que f (t) = tdeux est d'ordre exponentiel, puisque | tdeux| < e3t pour tout t> 0.
De manière formelle, nous avons le théorème suivant
Théorème (Conditions d'existence suffisantes)
Si f est une fonction partiellement continue pour t> 0 et d'ordre exponentiel c, alors il existe la transformée de Laplace pour s> c.
Il est important de noter qu'il s'agit d'une condition de suffisance, c'est-à-dire qu'il se pourrait qu'il y ait une fonction qui ne remplisse pas ces conditions et même si sa transformée de Laplace existe.
Un exemple de ceci est la fonction f (t) = t-1/2 qui n'est pas continue par morceaux pour t ≥ 0 mais sa transformée de Laplace existe.
Transformée de Laplace de certaines fonctions de base
Le tableau suivant montre les transformées de Laplace des fonctions les plus courantes.

Histoire
La transformation de Laplace doit son nom à Pierre-Simon Laplace, mathématicien et astronome théoricien français né en 1749 et mort en 1827. Sa renommée était telle qu'il était connu sous le nom de Newton de France.
En 1744, Leonard Euler consacra ses études aux intégrales avec la forme
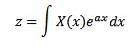
comme solutions d'équations différentielles ordinaires, mais il a rapidement abandonné cette enquête. Plus tard, Joseph Louis Lagrange, qui admirait beaucoup Euler, a également étudié ce type d'intégrales et les a reliées à la théorie des probabilités..
1782, Laplace
En 1782, Laplace a commencé à étudier ces intégrales comme des solutions aux équations différentielles et selon les historiens, en 1785, il a décidé de reformuler le problème, ce qui a plus tard donné naissance aux transformées de Laplace telles qu'elles sont comprises aujourd'hui..
Introduit dans le domaine de la théorie des probabilités, il n'intéressait guère les scientifiques de l'époque et n'était perçu que comme un objet mathématique n'ayant qu'un intérêt théorique..
Oliver Heaviside
C'est au milieu du XIXe siècle que l'ingénieur anglais Oliver Heaviside a découvert que les opérateurs différentiels peuvent être traités comme des variables algébriques, donnant ainsi à Laplace transforme leur application moderne..
Oliver Heaviside était un physicien, ingénieur électricien et mathématicien anglais né à Londres en 1850 et mort en 1925. Tout en essayant de résoudre des problèmes d'équation différentielle appliqués à la théorie des vibrations et en utilisant les études de Laplace, il a commencé à façonner les applications modernes des transformations de Laplace..
Les résultats présentés par Heaviside se sont rapidement répandus dans la communauté scientifique de l'époque, mais comme son travail n'était pas rigoureux, il a été rapidement critiqué par les mathématiciens plus traditionnels..
Cependant, l'utilité du travail de Heaviside dans la résolution d'équations en physique a rendu ses méthodes populaires auprès des physiciens et des ingénieurs..
Malgré ces revers et après quelques décennies de tentatives infructueuses, au début du XXe siècle, une justification rigoureuse pouvait être donnée aux règles de fonctionnement données par Heaviside..
Ces tentatives ont porté leurs fruits grâce aux efforts de divers mathématiciens tels que Bromwich, Carson, van der Pol, entre autres..
Propriétés
Parmi les propriétés de la transformée de Laplace, on distingue les suivantes:
Linéarité
Soit c1 et c2 des fonctions constantes et f (t) et g (t) dont les transformées de Laplace sont respectivement F (s) et G (s), alors on a:
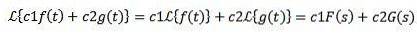
En raison de cette propriété, on dit que la transformée de Laplace est un opérateur linéaire.
Exemple
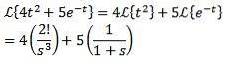
Premier théorème de traduction
S'il arrive que:
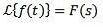
Et 'a' est n'importe quel nombre réel, donc:
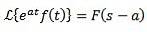
Exemple
Puisque la transformée de Laplace de cos (2t) = s / (s ^ 2 + 4) alors:
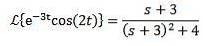
Deuxième théorème de traduction
Oui
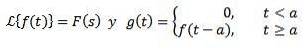
Ensuite
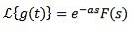
Exemple
Si f (t) = t ^ 3, alors F (s) = 6 / s ^ 4. Et donc la transformation de
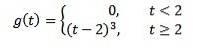
est G (s) = 6e-2 s/ s ^ 4
Changement d'échelle
Oui
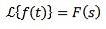
Et 'a' est un réel différent de zéro, nous devons
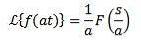
Exemple
Puisque la transformée de f (t) = sin (t) est F (s) = 1 / (s ^ 2 + 1) nous avons
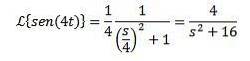
Transformée de Laplace des dérivés
Si f, f ', f ",…, f(n) sont continus pour t ≥ 0 et sont d'ordre exponentiel et f(n)(t) est continue par morceaux pour t ≥ 0, alors
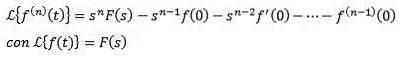
Transformée de Laplace des intégrales
Oui
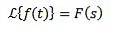
Ensuite
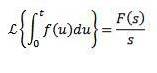
Multiplication par tn
Si nous devons
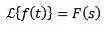
Ensuite
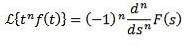
Division par t
Si nous devons
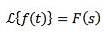
Ensuite
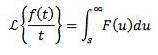
Fonctions périodiques
Soit f une fonction périodique de période T> 0, c'est-à-dire f (t + T) = f (t), alors
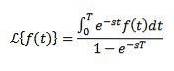
Comportement de F (s) lorsque s tend vers l'infini
Si f est continue en parties et d'ordre exponentiel et
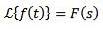
Ensuite
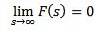
Transformations inverses
Lorsque nous appliquons la transformée de Laplace à une fonction f (t), nous obtenons F (s), qui représente ladite transformée. De la même manière, on peut dire que f (t) est la transformée de Laplace inverse de F (s) et s'écrit
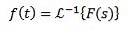
On sait que les transformées de Laplace de f (t) = 1 et g (t) = t sont F (s) = 1 / s et G (s) = 1 / sdeux respectivement, nous devons donc
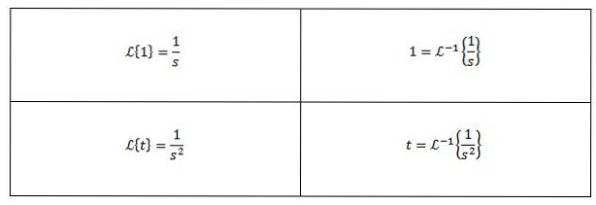
Certaines transformations de Laplace inverses courantes sont les suivantes

De plus, la transformée de Laplace inverse est linéaire, c'est-à-dire qu'il est vrai que
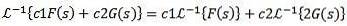
Exercer
Trouve
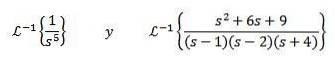
Pour résoudre cet exercice, nous devons faire correspondre la fonction F (s) avec l'un des tableaux précédents. Dans ce cas, si nous prenons n + 1 = 5 et en utilisant la propriété de linéarité de la transformée inverse, nous multiplions et divisons par 4! Obtenir
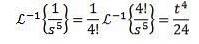
Pour la seconde transformation inverse, nous appliquons des fractions partielles pour réécrire la fonction F (s) puis la propriété de linéarité, obtenant
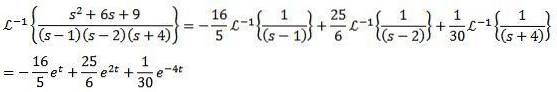
Comme nous pouvons le voir à partir de ces exemples, il est courant que la fonction F (s) évaluée ne correspond précisément à aucune des fonctions données dans le tableau. Pour ces cas, comme on peut le voir, il suffit de réécrire la fonction jusqu'à atteindre la forme appropriée.
Applications de la transformée de Laplace
Équations différentielles
La principale application des transformées de Laplace est de résoudre des équations différentielles.
En utilisant la propriété transform d'un dérivé, il est clair que
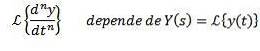
Et des n-1 dérivées évaluées à t = 0.
Cette propriété rend la transformée très utile pour résoudre les problèmes de valeur initiale où des équations différentielles à coefficients constants sont impliquées..
Les exemples suivants montrent comment utiliser la transformée de Laplace pour résoudre des équations différentielles.
Exemple 1
Compte tenu du problème de valeur initiale suivant
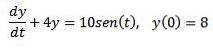
Utilisez la transformation de Laplace pour trouver la solution.
Nous appliquons la transformée de Laplace à chaque membre de l'équation différentielle
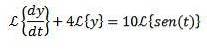
Par la propriété de la transformée d'un dérivé on a
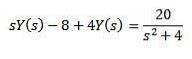
En développant toute l'expression et en effaçant Y (s), il nous reste
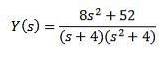
En utilisant des fractions partielles pour réécrire le côté droit de l'équation, nous obtenons
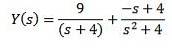
Enfin, notre objectif est de trouver une fonction y (t) qui satisfait l'équation différentielle. L'utilisation de la transformée de Laplace inverse nous donne le résultat
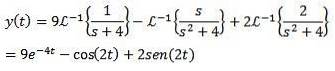
Exemple 2
Résoudre
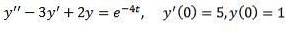
Comme dans le cas précédent, nous appliquons la transformation des deux côtés de l'équation et séparons terme par terme.
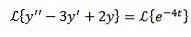
De cette façon, nous avons comme résultat
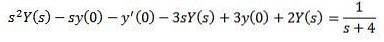
Substituer avec les valeurs initiales données et résoudre Y (s)
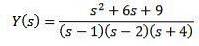
En utilisant des fractions simples, nous pouvons réécrire l'équation comme suit
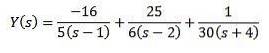
Et l'application de la transformée de Laplace inverse nous donne le résultat
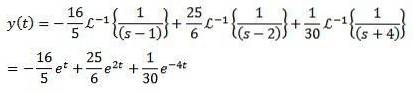
Dans ces exemples, vous pourriez arriver à la conclusion erronée que cette méthode n'est pas beaucoup mieux que les méthodes traditionnelles de résolution d'équations différentielles..
Les avantages de la transformée de Laplace sont que vous n'avez pas besoin d'utiliser la variation de paramètres ou de vous soucier des différents cas de la méthode des coefficients indéterminés..
De plus, lors de la résolution de problèmes de valeur initiale par cette méthode, nous utilisons dès le début les conditions initiales, il n'est donc pas nécessaire d'effectuer d'autres calculs pour trouver la solution particulière.
Systèmes d'équations différentielles
La transformée de Laplace peut également être utilisée pour trouver des solutions à des équations différentielles ordinaires simultanées, comme le montre l'exemple suivant.
Exemple
Démêler
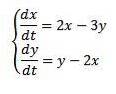
Avec les conditions initiales x (0) = 8 et y (0) = 3.
Si nous devons
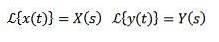
Ensuite
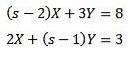
La résolution nous donne en conséquence
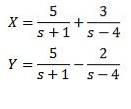
Et en appliquant la transformée de Laplace inverse, nous avons
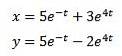
Mécanique et circuits électriques
La transformée de Laplace est d'une grande importance en physique, elle a principalement des applications pour la mécanique et les circuits électriques.
Un circuit électrique simple est composé des éléments suivants
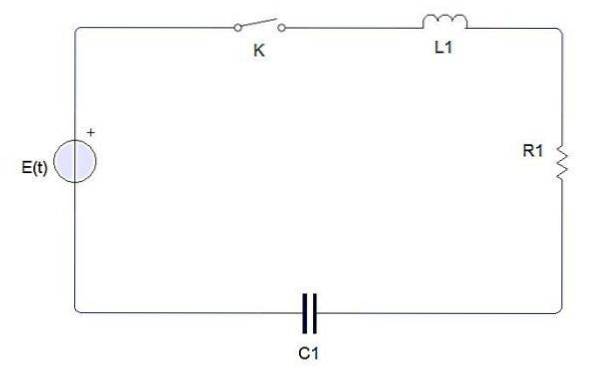
Un interrupteur, une batterie ou une source, un inducteur, une résistance et un condensateur. Lorsque l'interrupteur est fermé, un courant électrique est produit qui est noté i (t). La charge du condensateur est notée q (t).
Selon la deuxième loi de Kirchhoff, la tension produite par la source E vers le circuit fermé doit être égale à la somme de chacune des chutes de tension.
Le courant électrique i (t) est lié à la charge q (t) sur le condensateur par i = dq / dt. En revanche, la chute de tension dans chacun des éléments est définie comme suit:
La chute de tension à travers une résistance est iR = R (dq / dt)
La chute de tension à travers une inductance est L (di / dt) = L (ddeuxq / dtdeux)
La chute de tension à travers un condensateur est q / C
Avec ces données et en appliquant la deuxième loi de Kirchhoff au circuit fermé simple, on obtient une équation différentielle du second ordre qui décrit le système et nous permet de déterminer la valeur de q (t).
Exemple
Un inducteur, un condensateur et une résistance sont connectés à une batterie E, comme indiqué sur la figure. L'inductance est de 2 henries, le condensateur est de 0,02 farads et la résistance est de 16 ohms. Au temps t = 0, le circuit est fermé. Trouver la charge et le courant à tout instant t> 0 si E = 300 volts.
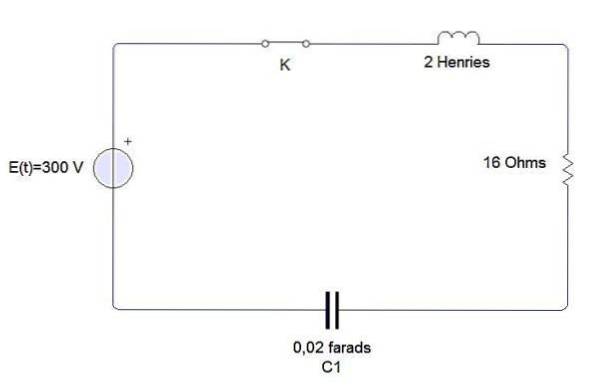
Nous avons que l'équation différentielle qui décrit ce circuit est la suivante
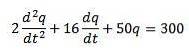
Où les conditions initiales sont q (0) = 0, i (0) = 0 = q '(0).
En appliquant la transformation de Laplace, nous obtenons cela
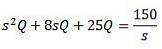
Et en résolvant Q (t)
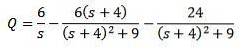
Ensuite, en appliquant la transformée de Laplace inverse, nous avons
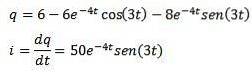
Les références
- G. Holbrook, J. (1987). Transformée de Laplace pour les ingénieurs en électronique. Limusa.
- Ruiz, L. M. et Hernandez, M. P. (2006). Equations différentielles et transformation de Laplace avec applications. Éditorial UPV.
- Simmons, G. F. (1993). Equations différentielles avec applications et notes historiques. McGraw-Hill.
- Spiegel, M. R. (1991). Laplace transforme. McGraw-Hill.
- Zill, D. G., et Cullen, M. R. (2008). Équations différentielles avec des problèmes de valeur limite. Cengage Learning Editores, S.A.


Personne n'a encore commenté ce post.