
Caractéristiques ovales (figure géométrique), exemples, exercices
le ovale symétrique est définie comme une courbe plate et fermée, qui a deux axes de symétrie perpendiculaires -un majeur et un mineur- et se compose de deux arcs de circonférence égaux deux par deux.
De cette manière, il peut être dessiné à l'aide d'une boussole et de quelques points de référence sur l'une des lignes de symétrie. Dans tous les cas, il existe plusieurs façons de le dessiner, comme nous le verrons plus tard.

C'est une courbe très familière, puisqu'elle est reconnue comme le contour d'une ellipse, ceci étant un cas particulier de l'ovale. Mais l'ovale n'est pas une ellipse, même s'il lui ressemble parfois beaucoup, car ses propriétés et sa disposition diffèrent. Par exemple, l'ellipse n'est pas construite avec une boussole.
Index des articles
- 1 Fonctionnalités
- 2 exemples
- 2.1 Construction d'un ovale à l'aide de cercles concentriques
- 3 exercices
- 3.1 - Exercice 1
- 3.2 - Exercice 2
- 4 Références
Caractéristiques
L'ovale a des applications très variées: l'architecture, l'industrie, le graphisme, l'horlogerie et la joaillerie ne sont que quelques domaines où son utilisation se démarque..
Les caractéristiques les plus remarquables de cette courbe importante sont les suivantes:
-Il appartient au groupe des courbes techniques: il est dessiné en formant des arcs circonférentiels à l'aide d'une boussole.
-Tous ses points sont sur le même plan.
-Manque de courbes ou de boucles.
-Sa disposition est continue.
-La courbe de l'ovale doit être lisse et convexe.
-Lorsque vous tracez une ligne tangente à l'ovale, tout est du même côté de la ligne.
-Un ovale n'admet que deux tangentes parallèles au plus.
Exemples
Il existe plusieurs méthodes de construction d'ovales qui nécessitent l'utilisation d'une règle, d'un carré et d'une boussole. Ensuite, nous allons mentionner certains des plus utilisés.
Construction d'un ovale à l'aide de cercles concentriques
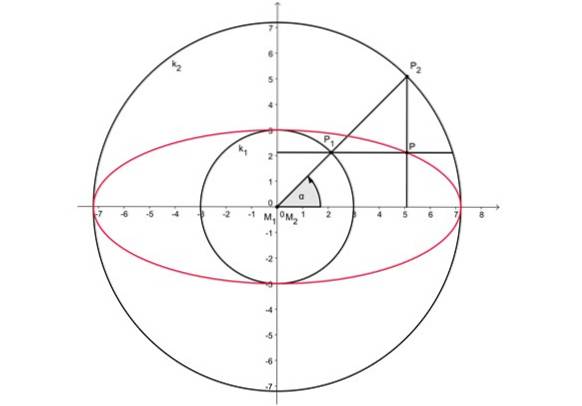
La figure 2 ci-dessus montre deux cercles concentriques centrés à l'origine. Le grand axe de l'ovale mesure le même que le diamètre de la circonférence extérieure, tandis que le petit axe correspond au diamètre de la circonférence intérieure.
-Un rayon arbitraire est dessiné vers la circonférence extérieure, qui coupe les deux cercles aux points P1 Et Pdeux.
-Puis le point P est projetédeux sur l'axe horizontal.
-De même, le point P est projeté1 sur l'axe vertical.
-L'intersection des deux lignes de projection est le point P et appartient à l'ovale.
-Tous les points de cette section de l'ovale peuvent être tracés de cette manière.
-Le reste de l'ovale est tracé avec la procédure analogue, effectuée dans chaque quadrant.
Exercices
Ensuite, d'autres manières de construire des ovales seront examinées, compte tenu d'une certaine mesure initiale, qui déterminera leur taille..
- Exercice 1
Dessinez à l'aide d'une règle et d'une boussole un ovale, dit grand axe, dont la longueur est de 9 cm.
Solution
Sur la figure 3, illustrée ci-dessous, l'ovale qui en résulte apparaît en rouge. Une attention particulière doit être portée aux lignes pointillées, qui sont les constructions auxiliaires nécessaires pour dessiner un ovale dont le grand axe est spécifié. Nous allons indiquer toutes les étapes nécessaires pour atteindre le dessin final.
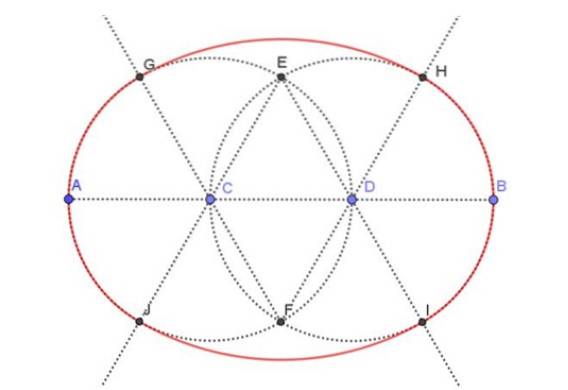
Étape 1
Dessinez avec une règle le segment AB de 9 cm.
Étape 2
Trisectez le segment AB, c'est-à-dire divisez-le en trois segments d'égale longueur. Le segment d'origine AB étant de 9 cm, les segments AC, CD et DB doivent mesurer chacun 3 cm.
Étape 3
Avec la boussole, centrage en C et ouverture CA, une circonférence auxiliaire est dessinée. De même, la circonférence auxiliaire de centre D et de rayon DB est dessinée avec la boussole..
Étape 4
Les intersections des deux cercles auxiliaires construits à l'étape précédente sont marquées. Nous l'appelons les points E et F.
Étape 5
Avec la règle, les rayons suivants sont dessinés: [FC), [FD), [EC), [ED).
Étape 6
Les rayons de l'étape précédente coupent les deux cercles auxiliaires aux points G, H, I, J respectivement.
Étape 7
Avec le centre de la boussole est fait en F et avec l'ouverture (ou le rayon) FG l'arc est dessiné GH. De même, en centrant en E et en rayon EI, l'arc est dessiné IJ.
Étape 8
L'union des arcades GJ, JI, IH Oui HG forme un ovale dont le grand axe est de 9 cm.
Étape 9
Nous procédons à effacer (masquer) les points et les lignes auxiliaires.
- Exercice 2
Dessinez un ovale avec une règle et une boussole, dont le petit axe est connu et sa mesure est de 6 cm.
Solution
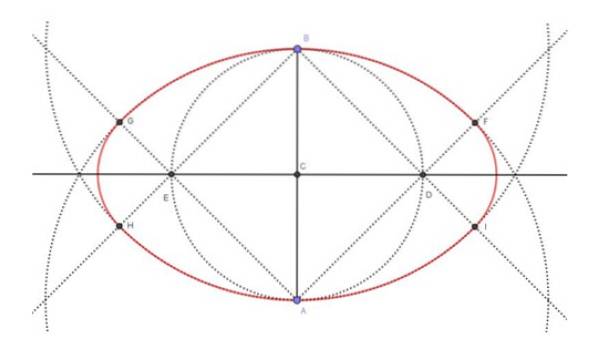
La figure ci-dessus (figure 4) montre le résultat final de la construction de l'ovale (en rouge), ainsi que les constructions intermédiaires nécessaires pour y accéder. Les étapes suivies pour construire l'ovale de petit axe de 6 cm étaient les suivantes:
Étape 1
Le segment AB de 6 cm de long est tracé avec la règle.
Étape 2
Avec la boussole et la règle, la bissectrice est tracée jusqu'au segment AB.
Étape 3
L'intersection de la bissectrice avec le segment AB aboutit au milieu C du segment AB.
Étape 4
Avec la boussole, la circonférence du centre C et le rayon CA sont dessinés.
Étape 5
La circonférence dessinée à l'étape précédente coupe la bissectrice de AB aux points E et D.
Étape 6
Les rayons [AD), [AE), [BD) et [BE) sont dessinés.
Étape 7
Avec la boussole, les circonférences du centre A et du rayon AB et celles du centre B et du rayon BA sont dessinées..
Étape 8
Les intersections des cercles dessinés à l'étape 7, avec les rayons construits à l'étape 6, déterminent quatre points, à savoir: F, G, H, I.
Étape 9
Avec le centre en D et le rayon DI, l'arc IF est dessiné. De la même manière, avec centre en E et rayon EG, l'arc GH est dessiné.
Étape 10
L'union des arcs de circonférence FG, GH, HI et IF détermine l'ovale souhaité.
Les références
- Ed Plastic. Courbes techniques: ovales, ovoïdes et spirales. Récupéré de: drajonavarres.wordpress.com.
- Mathematische Basteleien. Courbes d'œufs et ovales. Récupéré de: Mathematische-Basteleien.
- Université de Valence. Coniques et courbes techniques plates. Récupéré de: ocw.uv.es.
- Wikipédia. Ovale. Récupéré de: es.wikipedia.org.
- Wikipédia. Ovale. Récupéré de: en.wikipedia.org.

Personne n'a encore commenté ce post.