Formules de vitesse moyenne, comment il est calculé et exercice résolu

La vitesse moyenne pour une particule mobile, il est défini comme le rapport entre la variation de la position qu'elle subit et l'intervalle de temps utilisé dans le changement. La situation la plus simple est celle dans laquelle la particule se déplace le long d'une ligne droite représentée par l'axe des x..

Supposons que l'objet en mouvement occupe les positions x₁ et x_deux en temps t₁ et toi_deux respectivement. La définition de la vitesse moyenne v_m est représenté mathématiquement comme ceci:

Les unités de v_m dans le système international, ils sont en mètres / seconde (m / s). Les autres unités couramment utilisées qui apparaissent dans les textes et les appareils mobiles sont: km / h, cm / s, miles / h, pieds / s et plus, à condition qu'elles soient de la forme longueur / temps.

La lettre grecque «Δ» se lit «delta» et est utilisée pour indiquer brièvement la différence entre deux quantités..

Index des articles

• 1 Caractéristiques du vecteur vitesse moyenne vm
• 2 Les signes de la vitesse moyenne
• 3 Vitesse moyenne: une grandeur scalaire
• 4 Exercice résolu
• 5 Références

Caractéristiques du vecteur vitesse moyenne v_m

La vitesse moyenne est un vecteur, car elle est liée au changement de position, qui à son tour est connu sous le nom de vecteur de défilement.

Cette qualité est représentée en gras ou par une flèche au-dessus de la lettre qui désigne la grandeur. Cependant, dans une dimension, la seule direction possible est celle de l'axe des x et donc la notation vectorielle peut être supprimée.

Puisque les vecteurs ont une magnitude, une direction et un sens, un premier regard sur l'équation indique que la vitesse moyenne aura la même direction et le même sens que le déplacement..

Imaginez la particule dans l'exemple se déplaçant le long d'une ligne droite. Pour décrire son mouvement, il est nécessaire d'indiquer un point de référence, qui sera "l'origine" et sera noté O.

La particule peut se rapprocher ou s'éloigner de O, soit vers la gauche, soit vers la droite. Cela peut également prendre un temps long ou court pour arriver à une certaine position..

Les grandeurs qui ont été mentionnées: position, déplacement, intervalle de temps et vitesse moyenne, décrivent le comportement de la particule lorsqu'elle se déplace. Il s'agit des magnitudes cinématique.

Pour distinguer les positions ou emplacements à gauche de O, le signe (-) est utilisé et ceux à droite de O portent le signe (+).

La vitesse moyenne a une interprétation géométrique que l'on peut voir dans la figure suivante. C'est la pente de la ligne qui passe par les points P et Q. Lors de la coupe de la position de la courbe vs. temps en deux points, c'est une ligne droite séchage.

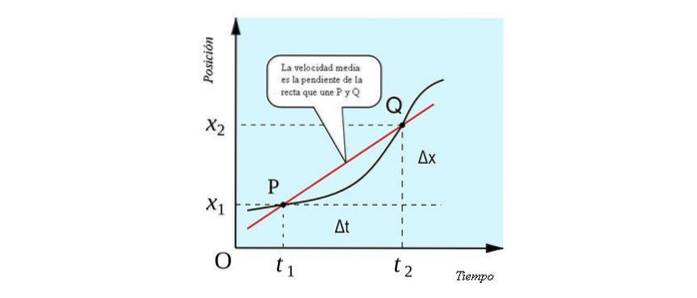
Les signes de la vitesse moyenne

Pour l'analyse suivante, il convient de tenir compte du fait que t_deux > t₁. Autrement dit, l'instant suivant est toujours supérieur à l'instant actuel. De cette manière t_deux - t₁ est toujours positif, ce qui a généralement du sens au quotidien.

Alors le signe de la vitesse moyenne sera déterminé par celui de X_deux - X₁. Notez qu'il est important d'être clair sur l'endroit où se trouve le point O -l'origine-, car c'est le point par rapport auquel la particule est dite aller "à droite" ou "à gauche".

Soit "en avant", soit "en arrière", selon la préférence du lecteur.

Si la vitesse moyenne est positive, cela signifie que En moyenne la valeur de "X«Augmente au fil du temps, bien que cela ne signifie pas qu'il peut avoir diminué à un moment donné de la période considérée. - Δt -.

Mais globalement, à la fin des temps Δt, elle a fini avec une position plus grande qu'elle avait au début. Les détails du mouvement sont ignorés dans cette analyse..

Et si la vitesse moyenne s'avère négative? Ensuite, cela signifie que la particule se termine par une coordonnée plus petite que celle avec laquelle elle a commencé. À peu près, il recula. Regardons quelques exemples numériques:

Exemple 1: Compte tenu des positions de départ et de fin indiquées, indiquez le signe de la vitesse moyenne. Où la particule s'est-elle déplacée dans le monde??

a) x₁ = 3 m; X_deux = 8 m

Répondre: X_deux- X₁  = 8 m - 3 m = 5 m. Vitesse moyenne positive, particule déplacée vers l'avant.

b) x₁ = 2 m; X_deux = -3 m

Répondre: X_deux - X₁ = -3 m - 2 m = -5 m. Vitesse moyenne négative, la particule s'est déplacée vers l'arrière.

 c) x₁  = - 5 m; X_deux = -12 m

Répondre: X_deux - X₁   = -12 m - (-5 m) = -7 m. Vitesse moyenne négative, la particule s'est déplacée vers l'arrière.

d) x₁  = - 4 m; X_deux = 10 m

Répondre: X_deux - X₁  = 10 m - (-4 m) = 14 m. Vitesse moyenne positive, particule déplacée vers l'avant.

La vitesse moyenne peut-elle être égale à 0? Oui, à condition que le point de départ et le point d'arrivée soient les mêmes. Cela signifie-t-il que la particule était nécessairement au repos tout le temps??

Non, cela signifie simplement que le voyage était aller-retour. Peut-être qu'il a voyagé rapidement ou peut-être très lentement. Pour l'instant ce n'est pas connu.

Vitesse moyenne: une quantité scalaire

Cela nous amène à définir un nouveau terme: vitesse moyenne. En physique, il est important de faire la distinction entre les quantités vectorielles et les quantités non vectorielles: scalaires.

Pour la particule qui a fait l'aller-retour, la vitesse moyenne est de 0, mais elle peut ou non avoir été très rapide. Pour le savoir, la vitesse moyenne est définie comme:

Les unités de vitesse moyenne sont les mêmes que celles de vitesse moyenne. La différence fondamentale entre les deux grandeurs est que la vitesse moyenne comprend des informations intéressantes sur la direction et le sens de la particule..

En revanche, la vitesse moyenne ne fournit que des informations numériques. Avec lui, on sait à quelle vitesse ou lentement la particule s'est déplacée, mais pas si elle s'est déplacée vers l'avant ou vers l'arrière. C'est donc une grandeur scalaire. Comment les distinguer en les dénotant? Une façon est de laisser le gras pour les vecteurs, ou en plaçant une flèche sur eux.

Et il est important de noter que la vitesse moyenne ne doit pas nécessairement être égale à la vitesse moyenne. Pour l'aller-retour, la vitesse moyenne est nulle, mais la vitesse moyenne ne l'est pas. Les deux ont la même valeur numérique lorsqu'ils voyagent toujours dans la même direction.

Exercice résolu

Vous rentrez de l'école tranquillement à 95 km / h sur 130 km. Il commence à pleuvoir et ralentit à 65 km / h. Il rentre enfin à la maison après avoir conduit pendant 3 heures et 20 minutes.

a) À quelle distance se trouve votre domicile de l'école?

b) Quelle était la vitesse moyenne?

Réponses:

a) Quelques calculs préliminaires sont nécessaires:

Le voyage est divisé en deux parties, la distance totale est:

d = d1 + d_deux, avec d1 = 130 km

t2 = 3,33 - 1,37 heure = 1,96 heure

Calcul de d_deux:

ré_deux = 65 km / h x 1,96 h = 125,4 km.

L'école est distante d1 + d_deux = 255,4 km de la maison.

b) Nous pouvons maintenant trouver la vitesse moyenne:

Les références

1. Giancoli, D. Physique. Principes avec applications. Sixième édition. Prentice Hall. 21-22.
2. Resnick, R. (1999). Physique. Volume 1. Troisième édition en espagnol. Mexique. Compañía Editorial Continental S.A. de C.V. 20-21.
3. Serway, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7ma. Édition. Mexique. Éditeurs d'apprentissage Cengage. 21-23.