
Définition de l'accélération centripète, formules, calculs, exercices
La accélération centripète àc, Aussi appelée radiale ou normale, c'est l'accélération que porte un objet en mouvement lorsqu'il décrit une trajectoire circulaire. Son ampleur est vdeux/ r, où r est le rayon du cercle, il est dirigé vers le centre de celui-ci et se charge de maintenir le mobile sur son chemin.
Les dimensions de l'accélération centripète sont la longueur par unité de temps au carré. Dans le système international, ils sont m / sdeux. Si, pour une raison quelconque, l'accélération centripète disparaît, il en va de même pour la force qui force le mobile à maintenir la trajectoire circulaire.

C'est ce qui arrive à une voiture essayant de prendre un virage sur une piste plate et verglacée, où le frottement entre le sol et les roues est insuffisant pour que la voiture puisse prendre un virage. Par conséquent, la seule possibilité qui reste est de se déplacer en ligne droite et c'est pourquoi il quitte la courbe.
Index des articles
- 1 Mouvements circulaires
- 2 La force centripète
- 3 formules d'accélération centripète
- 4 Exercice résolu
- 4.1 Réponse
- 5 Références
Mouvements circulaires
Lorsqu'un objet se déplace en cercle, à tout moment l'accélération centripète est dirigée radialement vers le centre de la circonférence, une direction perpendiculaire à la trajectoire suivie.
Puisque la vitesse est toujours tangente à la trajectoire, alors la vitesse et l'accélération centripète s'avèrent être perpendiculaires. Par conséquent, la vitesse et l'accélération n'ont pas toujours la même direction.
Dans ces circonstances, le mobile a la possibilité de décrire la circonférence à vitesse constante ou variable. Le premier cas est connu sous le nom de mouvement circulaire uniforme ou MCU pour son acronyme, le second cas sera un mouvement circulaire variable.
Dans les deux cas, l'accélération centripète est responsable du maintien de la rotation du mobile, garantissant que la vitesse ne varie que dans la direction et dans la direction.
Cependant, pour avoir un mouvement circulaire variable, une autre composante de l'accélération dans le même sens de la vitesse serait nécessaire, qui est chargée d'augmenter ou de diminuer la vitesse. Cette composante de l'accélération est connue sous le nom de accélération tangentielle.
Le mouvement circulaire variable et le mouvement curviligne en général ont les deux composants de l'accélération, car le mouvement curviligne peut être imaginé comme le chemin à travers d'innombrables arcs circonférentiels qui composent le chemin courbe..
La force centripète
Désormais, une force est chargée de fournir l'accélération. Pour un satellite en orbite autour de la Terre, c'est la force de gravité. Et comme la gravité agit toujours perpendiculairement à la trajectoire, elle ne modifie pas la vitesse du satellite..
Dans un tel cas, la gravité agit comme un force centripète, qui n'est pas une classe de force spéciale ou distincte, mais qui, dans le cas du satellite, est dirigée radialement vers le centre de la terre.
Dans d'autres types de mouvement circulaire, par exemple une voiture qui tourne une courbe, le rôle de la force centripète est joué par le frottement statique et pour une pierre attachée à une corde qui tourne en cercles, la tension dans la corde est la force qui force le mobile à faire tourner.
Formules d'accélération centripète
L'accélération centripète est calculée par l'expression:
ac = vdeux/ r
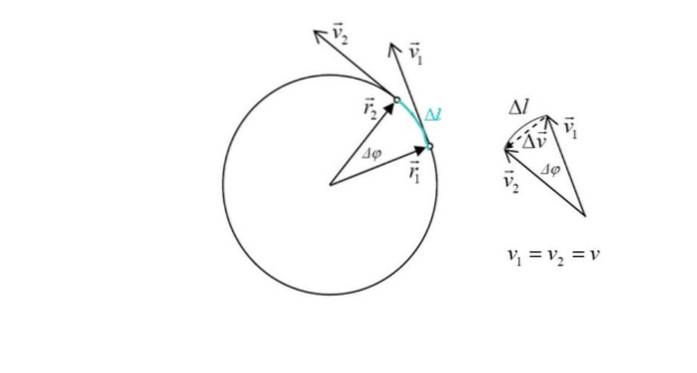
Cette expression sera dérivée ci-dessous. Par définition, l'accélération est le changement de vitesse dans le temps:

Le mobile prend un temps Δt dans l'itinéraire, qui est petit, car les points sont très proches.
La figure montre également deux vecteurs de position r1 Oui rdeux, dont le module est le même: le rayon r de la circonférence. L'angle entre les deux points est Δφ. En vert met en évidence le arc traversé par le mobile, noté Δl.
Sur la figure de droite, on voit que la grandeur de Δv, le changement de vitesse est à peu près proportionnel à Δl, car l'angle Δφ est petit. Mais le changement de vitesse est précisément lié à l'accélération. À partir du triangle, on peut le voir, en ajoutant les vecteurs que:
v1 + Δv = vdeux → Δv = vdeux - v1
Δv c'est intéressant, car il est proportionnel à l'accélération centripète. D'après la figure, on peut voir que puisque l'angle Δφ est petit, le vecteur Δv est essentiellement perpendiculaire aux deux v1 aimer vdeux et pointe vers le centre de la circonférence.
Bien que jusqu'à présent les vecteurs soient surlignés en gras, pour les effets de nature géométrique qui suivent, nous travaillons avec les modules ou grandeurs de ces vecteurs, en supprimant la notation vectorielle.
Autre chose: vous devez utiliser la définition de l'angle central, qui est:
Δφ= Δg / D
Maintenant, les deux chiffres sont comparés, qui sont proportionnels puisque l'angle Δφ il est courant:

Diviser par Δt:

àc= vdeux/ r
Exercice résolu
Une particule se déplace dans un cercle de rayon 2,70 m. À un instant donné, son accélération est de 1,05 m / sdeux dans une direction faisant un angle de 32,0 ° avec la direction du mouvement. Calculez votre vitesse:
a) À ce moment-là
b) 2,00 secondes plus tard, en supposant une accélération tangentielle constante.
Répondre
C'est un mouvement circulaire varié, puisque l'énoncé indique que l'accélération a un angle donné avec la direction du mouvement qui n'est ni 0º (il ne pourrait pas s'agir d'un mouvement circulaire) ni 90º (ce serait un mouvement circulaire uniforme).
Par conséquent, les deux composantes - radiale et tangentielle - coexistent. Ils seront désignés parc déjàt et sont dessinés dans la figure suivante. Le vecteur en vert est le vecteur d'accélération nette ou simplement l'accélération à.

a) Calcul des composantes d'accélération
àc = a.cos θ = 1,05 m / sdeux . cos 32,0 ° = 0,89 m / sdeux (en rouge)
àt = a.sen θ = 1,05 m / sdeux . sin 32,0 ° = 0,57 m / sdeux (en orange)
Calcul de la vitesse du mobile
Depuis unc = vdeux/ r, ensuite:
v = vou alors +àt. t = 1,6 m / s + (0,57 x 2) m / s = 2,74 m / s
Les références
- Giancoli, D. Physique. 2006. Principes avec applications. Sixième édition. Prentice Hall. 107-108.
- Hewitt, Paul. 2012. Science physique conceptuelle. Cinquième édition.Pearson 106 - 108.

Personne n'a encore commenté ce post.